 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Общий подход и алгоритмы моделирования случайных процессов
|
|
Теоретические основы и практические вопросы разработки алгоритмов имитационного моделирования случайных процессов подробно и достаточно глубоко рассматриваются в ряде известных работ. В основе моделирования случайных процессов различных видов обычно лежит использование модели гауссового (нормального) стационарного процесса (ГСП) 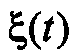 с математическим ожиданием
с математическим ожиданием  и с известной корреляционной функцией
и с известной корреляционной функцией 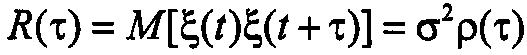 , где
, где 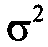 – дисперсия, а
– дисперсия, а 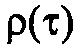 нормированная функция корреляции процесса. Вместо функции
нормированная функция корреляции процесса. Вместо функции 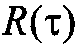 может быть изначально задана однозначно связанная с ней спектральная плотность мощности процесса
может быть изначально задана однозначно связанная с ней спектральная плотность мощности процесса 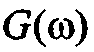 .
.
Реализацию процесса 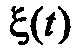 будем обозначать символом –
будем обозначать символом – 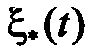 , т. е. помечаемую произвольным индексом *. При использовании цифровой ЭВМ разрабатываемая модель ГСП должна обеспечивать генерацию таких реализаций в дискретном времени для случайной последовательности
, т. е. помечаемую произвольным индексом *. При использовании цифровой ЭВМ разрабатываемая модель ГСП должна обеспечивать генерацию таких реализаций в дискретном времени для случайной последовательности 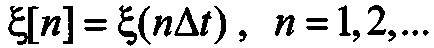 с заданным интервалом дискретизации Δ t. Имея реализации ГСП и выполняя над ними различного рода линейные и нелинейные преобразования, можно получить (также в дискретном времени) реализации негауссового случайного процесса с заданным законом распределения и корреляционной функцией. Таким образом, модель и формируемый на ее основе алгоритм генерации ГСП являются базовыми для получения моделей и алгоритмов генерации случайных процессов других видов.
с заданным интервалом дискретизации Δ t. Имея реализации ГСП и выполняя над ними различного рода линейные и нелинейные преобразования, можно получить (также в дискретном времени) реализации негауссового случайного процесса с заданным законом распределения и корреляционной функцией. Таким образом, модель и формируемый на ее основе алгоритм генерации ГСП являются базовыми для получения моделей и алгоритмов генерации случайных процессов других видов.
Модель ГСП почти всегда базируется на выполнении некоторого линейного преобразования совокупности значений независимых гауссовых случайных величин 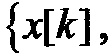
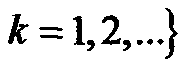 в последовательность
в последовательность 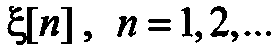 коррелированную по заданному закону. Рассмотрим возможные варианты применения данного подхода.
коррелированную по заданному закону. Рассмотрим возможные варианты применения данного подхода.
Алгоритм генерации реализации случайного процесса как реализации случайного вектора. Простейшим способом получения реализации ГСП 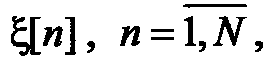 конечной длины является ее представление как реализации случайного вектора
конечной длины является ее представление как реализации случайного вектора 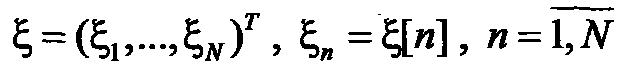 с матрицей:
с матрицей:
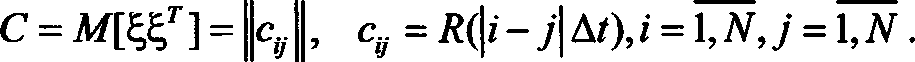
Тогда, как известно, вектор 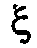 может быть получен на основе линейного преобразования вектора х, компоненты которого являются независимыми гауссовыми стандартными случайными величинами
может быть получен на основе линейного преобразования вектора х, компоненты которого являются независимыми гауссовыми стандартными случайными величинами
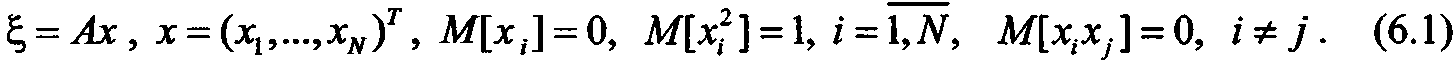 13.1
13.1
Здесь матрица А, выполняющая линейное преобразование, удовлетворяет уравнению ААТ = С.
Матрица А является нижней треугольной матрицей 
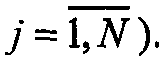 Подобное представление называется факторизацией ковариационной матрицы (факторизацией Холецкого). При выполнении такого преобразования
Подобное представление называется факторизацией ковариационной матрицы (факторизацией Холецкого). При выполнении такого преобразования 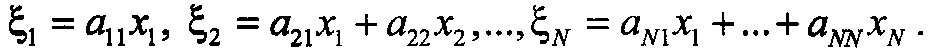 .
.
С учетом того, что 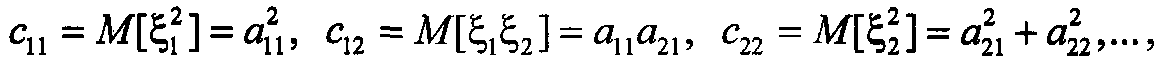 определение ненулевых элементов матрицы А может производиться на основе подобных уравнений, связывающих элементы матрицы ковариации С с элементами матрицы А, последовательно в виде:
определение ненулевых элементов матрицы А может производиться на основе подобных уравнений, связывающих элементы матрицы ковариации С с элементами матрицы А, последовательно в виде:
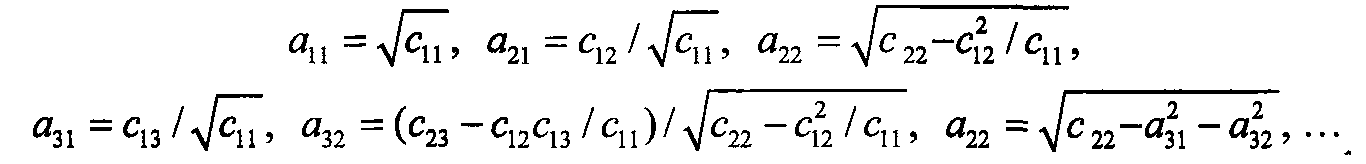
Следует отметить, что при выполнении преобразования (13.1) для случая негауссового вектора х с теми же параметрами вектор 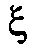 будет иметь негауссово распределение с таким же (нулевым) математическим ожиданием и матрицей ковариации С.
будет иметь негауссово распределение с таким же (нулевым) математическим ожиданием и матрицей ковариации С.
Использование рассмотренного подхода к генерации реализаций ГСП как реализаций случайного вектора с заданной ковариационной матрицей обладает одним недостатком: размерность генерируемого вектора и, соответственно, длина получаемой реализации ГСП ограничены. Это связано с тем, что выполнение разложения Холецкого для матриц ковариации больших размеров требует больших вычислительных ресурсов, а в некоторых случаях может происходить утрата свойств положительной определенности за счет потери значимости при выполнении вычислений. В этом случае точное решение для матрицы А при достаточно больших значениях N может быть не найдено, что требует проведения дополнительного анализа.
Алгоритм скользящей суммы (СС). Другой известный подход к моделированию ГСП состоит в том, что по отношению к совокупности независимых значений стандартной гауссовой случайной величины { x [ k ]} при получении последовательности 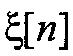 , коррелированной по заданному закону, выполнятся линейное преобразование, которое записывается в виде СС:
, коррелированной по заданному закону, выполнятся линейное преобразование, которое записывается в виде СС:
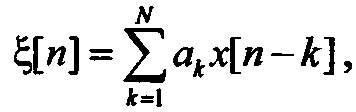 (13.2)
(13.2)
где 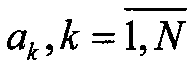 - совокупность коэффициентов, которые при построении алгоритма нужно найти исходя из вида корреляционной функции R(τ). Уравнение (13.2) описывает реакцию линейного фильтра с передаточной в смысле дискретного преобразования Лапласа (z -преобразования) характеристикой
- совокупность коэффициентов, которые при построении алгоритма нужно найти исходя из вида корреляционной функции R(τ). Уравнение (13.2) описывает реакцию линейного фильтра с передаточной в смысле дискретного преобразования Лапласа (z -преобразования) характеристикой 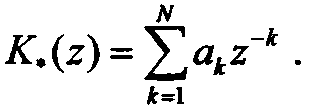
Для решения указанной задачи возможно применение различных подходов и методов, как аналитических, так и численных.
Рассмотрим сначала метод разложения спектральной плотности, использование которого позволяет в ряде случаев получить аналитические соотношения для расчета коэффициентов 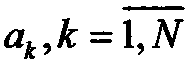 . Пусть вместо функции
. Пусть вместо функции 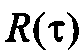 изначально дан энергетический спектр процесса
изначально дан энергетический спектр процесса 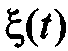
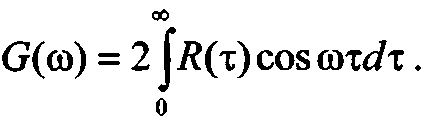
Пусть также расположение 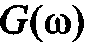 на оси частот ограничено интервалом
на оси частот ограничено интервалом 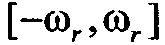 , т. е.
, т. е. 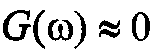 , при
, при 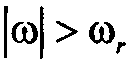 . Тогда
. Тогда 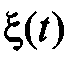 можно рассматривать как результат воздействия ГСП x(t) с энергетическим спектром
можно рассматривать как результат воздействия ГСП x(t) с энергетическим спектром 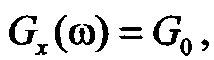
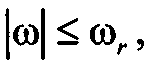
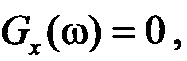
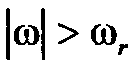 на линейную систему с импульсной характеристикой
на линейную систему с импульсной характеристикой  где
где 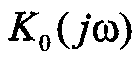 - частотная передаточная функция, удовлетворяющая соотношению
- частотная передаточная функция, удовлетворяющая соотношению 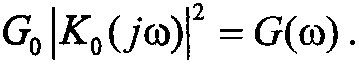 Тогда, используя разложение
Тогда, используя разложение  и x(t) в ряд Котельникова с шагом
и x(t) в ряд Котельникова с шагом 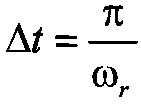 , можно получить:
, можно получить:
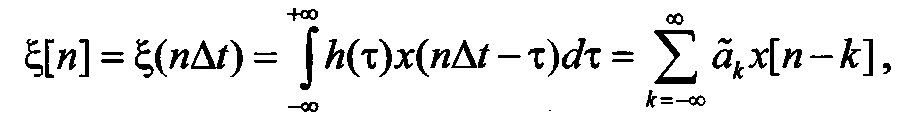 (13.3)
(13.3)
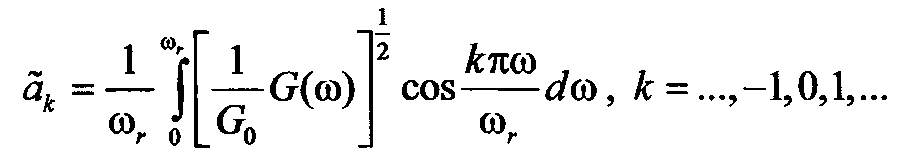
С учетом условия нормировки для мощности входного процесса 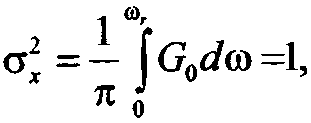
 и быстрой сходимости значений
и быстрой сходимости значений 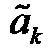 к нулю при
к нулю при 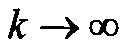 окончательно можно получить искомую форму алгоритма моделирования
окончательно можно получить искомую форму алгоритма моделирования 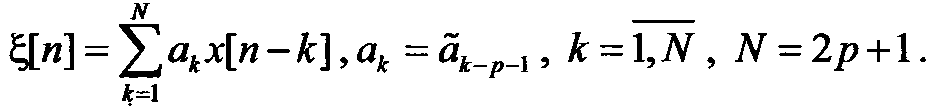
Параметр р здесь ограничивает число весовых коэффициентов ряда (13.3) с методической погрешностью 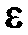 :
: 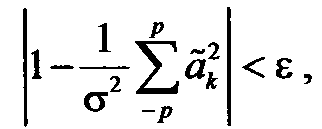 где
где 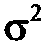 дисперсия
дисперсия 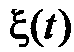 .
.
Рассмотренный метод приводит к приближенным формулам для определения коэффициентов скользящего суммирования и требует анализа уровня погрешности исходя из соотношения параметров корреляционной функции, интервала дискретизации и количества коэффициентов скользящей суммы. Кроме того, полученные при интегрировании выражения могут быть использованы не для всех ситуаций, что также требует проведения дополнительного анализа.
Более общим представляется численный метод получения коэффициентов скользящей суммы путем решения системы нелинейных уравнений, связывающих значения корреляционной функции и коэффициенты СС. Очевидно, что перемножая 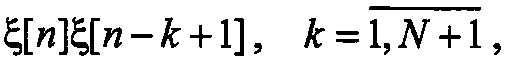 и выполняя соответствующие операции усреднения
и выполняя соответствующие операции усреднения 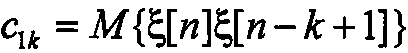 , можно записать:
, можно записать:
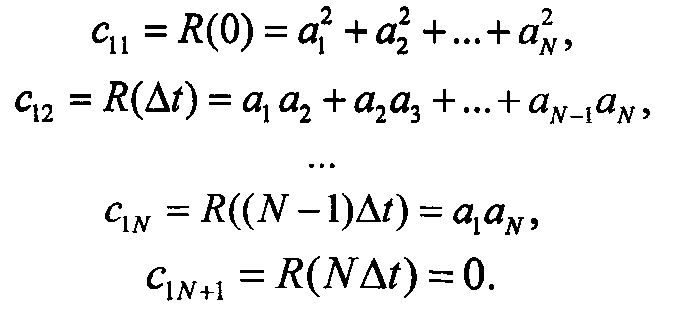
В матричном виде эту систему можно переписать таким образом:
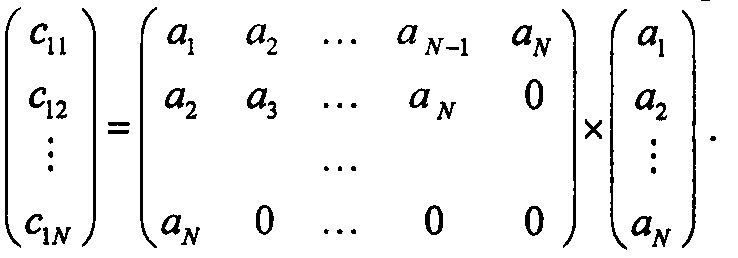 (13.4)
(13.4)
Искомые коэффициенты при известной корреляционной функции могут быть получены путем решения матричного нелинейного уравнения вида (13.4). В ставшей уже классической работе указывалось, что решение данной системы связано с определенными трудностями вычислительного характера. Следует также отмстить, что уравнения (13.4) однозначно позволяют решить обратную задачу – нахождения значений корреляционной функции по коэффициентам СС.
Алгоритм авторегрессии – скользящей суммы (АР-СС). Данный алгоритм при генерации ГСП в общем случае реализует рекуррентное уравнение вида:
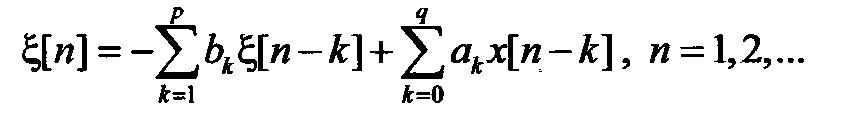 (13.5)
(13.5)
Модель процесса в форме (13.5) называется моделью авторегрессии – скользящей суммы, так как в ней комбинируется первая часть, являющаяся авторегрессией для 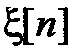 , и вторая часть, реализующая вычисление СС для входной последовательности независимых гауссовых стандартных величин { x [ k ]}. В итоге, уравнение (13.5) описывает реакцию линейного фильтра с передаточной в смысле дискретного преобразования Лапласа (z -преобразования) характеристикой
, и вторая часть, реализующая вычисление СС для входной последовательности независимых гауссовых стандартных величин { x [ k ]}. В итоге, уравнение (13.5) описывает реакцию линейного фильтра с передаточной в смысле дискретного преобразования Лапласа (z -преобразования) характеристикой
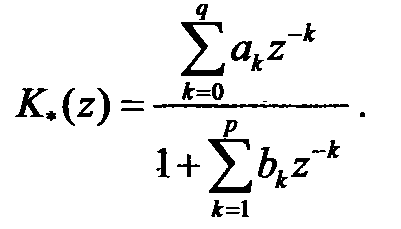 (13.6)
(13.6)
Задача построения модели ГСП состоит в нахождении коэффициентов ак и bк по виду корреляционной функции 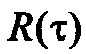 . Для получения алгоритмов данного класса также возможно применение как аналитических, так и численных методов.
. Для получения алгоритмов данного класса также возможно применение как аналитических, так и численных методов.
Рекуррентные алгоритмы (13.5) пригодны для моделирования процессов 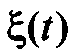 с рациональной спектральной плотностью
с рациональной спектральной плотностью 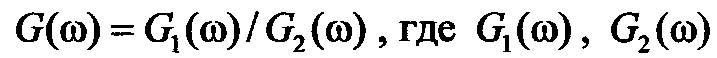 - полиномы степени q' и р' относительно ω. Такой процесс получается при прохождении гауссового белого шума через линейную систему с сосредоточенными параметрами и передаточной функцией
- полиномы степени q' и р' относительно ω. Такой процесс получается при прохождении гауссового белого шума через линейную систему с сосредоточенными параметрами и передаточной функцией 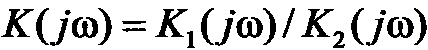 , где
, где 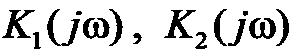 полиномы относительно j ω степени q и р > 1.
полиномы относительно j ω степени q и р > 1.
Рассмотрим получение алгоритма вида (13.5) методом факторизации. В этом методе для нахождения K *(z) = A (z) /B (z) передаточной функции, формирующей соответствующий дискретный процесс 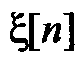 , необходимо сначала найти его спектральную плотность:
, необходимо сначала найти его спектральную плотность: 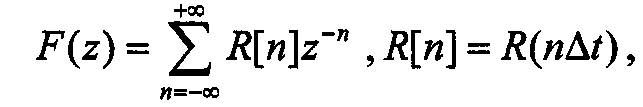 а затем с учетом того, что
а затем с учетом того, что 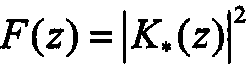 , провести факторизацию, т. е. представить с помощью алгебраического разложения полиномов в виде сомножителей
, провести факторизацию, т. е. представить с помощью алгебраического разложения полиномов в виде сомножителей
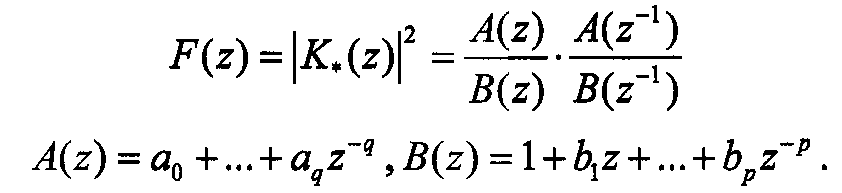
Для получения F(z) удобно воспользоваться соотношением 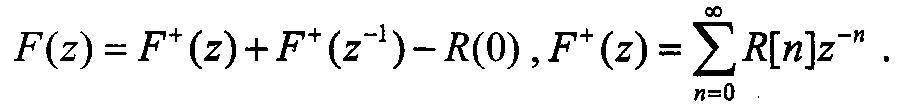
Дата публикования: 2015-09-17; Прочитано: 1371 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
