 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Префиксные коды
|
|
Простейшими кодами, на основе которых может выполняться сжатие данных, являются коды без памяти. В коде без памяти каждый символ в кодируемом векторе данных заменяется кодовым словом из префиксного множества двоичных последовательностей или слов.
Префиксным множеством двоичных последовательностей S называется конечное множество двоичных последовательностей, таких, что ни одна последовательность в этом множестве не является префиксом, или началом, никакой другой последовательности в S.
К примеру, множество двоичных слов S1 = {00, 01, 100, 110, 1010, 1011 } является префиксным множеством двоичных последовательностей, поскольку, если проверить любую из возможных совместных комбинаций (wi wj) из S1, то видно, что wi никогда не явится префиксом (или началом) wj. С другой стороны, множество S2 = { 00, 001, 1110 } не является префиксным множеством двоичных последовательностей, так как последовательность 00 является префиксом (началом) другой последовательности из этого множества - 001.
Таким образом, если необходимо закодировать некоторый вектор данных X = (x1, x2,… xn) с алфавитом данных А размера N, то кодирование кодом без памяти осуществляется следующим образом:
- составляют полный список символов a1, a2, aj...,aN алфавита А, в котором aj - j -й по частоте появления в X символ, то есть первым в списке будет стоять наиболее часто встречающийся в алфавите символ, вторым – реже встречающийся и т.д.;
- каждому символу aj назначают кодовое слово wj из префиксного множества двоичных последовательностей S;
- выход кодера получают объединением в одну последовательность всех полученных двоичных слов.
Формирование префиксных множеств и работа с ними – это отдельная серьезная тема из теории множеств, выходящая за рамки нашего курса, но несколько необходимых замечаний все-таки придется сделать.
Если S ={ w1, w2,..., wN } - префиксное множество, то можно определить некоторый вектор 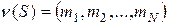 , состоящий из чисел, являющихся длинами соответствующих префиксных последовательностей (mi - длина wi ).
, состоящий из чисел, являющихся длинами соответствующих префиксных последовательностей (mi - длина wi ).
Вектор 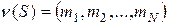 , состоящий из неуменьшающихся положительных целых чисел, называется вектором Крафта. Для него выполняется неравенство
, состоящий из неуменьшающихся положительных целых чисел, называется вектором Крафта. Для него выполняется неравенство
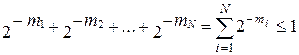 . (8.10)
. (8.10)
Это неравенство называется неравенством Крафта. Для него справедливо следующее утверждение: если S - какое-либо префиксное множество, то v(S) - вектор Крафта.
Иными словами, длины двоичных последовательностей в префиксном множестве удовлетворяют неравенству Крафта.
Если неравенство (8.10) переходит в строгое равенство, то такой код называется компактным и обладает наименьшей среди кодов с данным алфавитом длиной, то есть является оптимальным.
Ниже приведены примеры простейших префиксных множеств и соответствующие им векторы Крафта:
S1 = {0, 10, 11} и v(S1) = (1, 2, 2);
S2 = {0, 10, 110, 111} и v(S2) = (1, 2, 3, 3 );
S3 = {0, 10, 110, 1110, 1111} и v(S3) = (1, 2, 3, 4, 4);
S4 = {0, 10, 1100, 1101, 1110, 1111} и v(S4) = (1, 2, 4, 4, 4, 4);
S5 = {0, 10, 1100, 1101, 1110, 11110, 11111} и v(S5) = (1, 2, 4, 4, 4, 5, 5);
S6 = {0, 10, 1100, 1101, 1110, 11110, 111110, 111111}
и v(S6) = (1,2,4,4,4,5,6,6).
Допустим мы хотим разработать код без памяти для сжатия вектора данных X = (x1, x2,… xN) с алфавитом А размером в N символов. Введем в рассмотрение так называемый вектор вероятностей 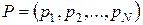 , где
, где 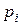 - вероятность появления i -го символа из А в X или вектор частот F = (f1, f2,..., fN), где fi - количество появлений i -го символа из А в X. Закодируем X кодом без памяти.
- вероятность появления i -го символа из А в X или вектор частот F = (f1, f2,..., fN), где fi - количество появлений i -го символа из А в X. Закодируем X кодом без памяти.
Длина двоичной кодовой последовательности на выходе кодера составит
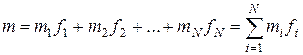 , (8.11)
, (8.11)
а средняя длина двоичной кодовой последовательности на выходе кодера составит
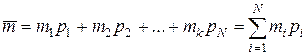 . (8.12)
. (8.12)
Лучшим кодом без памяти был бы код, для которого средняя длина 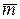 - минимальна. Для разработки такого кода нам нужно найти вектор Крафта, для которого
- минимальна. Для разработки такого кода нам нужно найти вектор Крафта, для которого 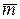 была бы минимальной.
была бы минимальной.
Простой перебор возможных вариантов - вообще-то, не самый лучший способ найти такой вектор Крафта, особенно для большого 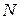 .
.
Дата публикования: 2015-09-17; Прочитано: 1135 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
