Золотого эллиптического торса

(рис.15.12, 15.13)

Традиционно поверхности одинакового ската конструируются при помощи коничес-кой поверхности с заданным уклоном её об-разующих, вершина которой перемещается по заданной плоской или пространствен-ной кривой (см. рис.15.8, 15.9). Тогда ис-комая поверхность торса, огибая последо-вательные положения образующего конуса, формирует фигуру его горизонтального следа как линию, огибающую последовате-льные положения основания подвижного конуса. Такая задача характерна для проек-тирования откосов насыпей и выемок доро-жного полотна, когда по условию задана бровка дороги.

При проектировании кровель зданий скаты которых должны иметь одинаковый уклон (см. рис. 11.21) исходным условием являются фигуры их горизонтальных карни-зов. Тогда возникает задача, обратная вы-шеописанной: по фигуре основания-карниза построить фигуру бровки-конька.

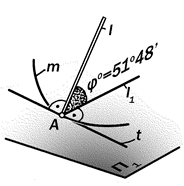
Если представить фигуру карниза зда-ния в виде золотого эллипса (см. рис.13.37), то из каждой его точки должны начинаться образующие прямые линии, составляющие с горизонтальной плоскостью постоянный угол j° = 51°50¢, равный углу наклона граней пирамиды фараона Хеопса к плос-кости его основания. Графически этот угол содержится в структуре золотого эллипса (рис.15.10).

В отличии от прямой задачи, в которой формообразующим элементом была подви-жная коническая поверхность заданной вы-соты, в данной задаче формообразующим конструктивом является трёхэлементная линейная структура, состоящая из наклон-ной под заданным углом линии l и её гори-зонтальной проекции l₁, которые перпенди-кулярны к горизонтальной прямой t. Если

прямую t перемещать касательно к линии m

Рис. 15.10 Геометрическая модель формообразующей конструкции

золотого торса

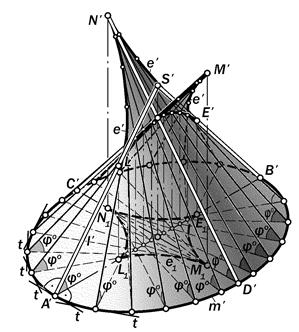
Рис.15.11. Геометрическая модель

золотого эллиптического торса

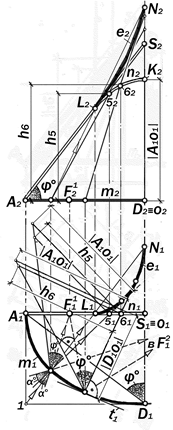
Рис.15. 13. Графика построения фрон-тальной проекции гребня n и ребра

возврата поверхности золотого

эллиптического торса

эллиптического торса

золотого эллипса,то линия l будет образо-

вывать искомую поверхность, а её гори-зонтальная проекция l₁ будет занимать по-ложения нормалей к линии эллипса в точ-ках касания к ней прямой t.

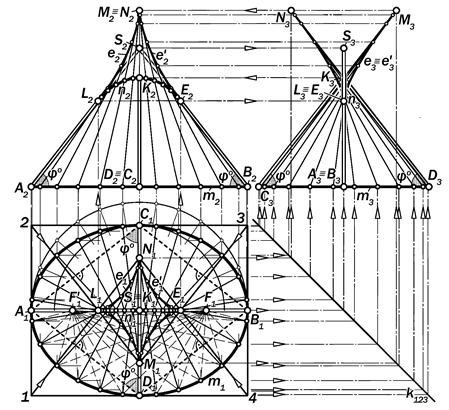
Рис.15.12. Графическая модель золотого эллиптического торса

Это обстоятель-

ство позволяет одно-

значно построить 3-х

картинный комплекс-

ный чертёж золотого

эллиптическог торса

Для этого необ-

ходимо (рис.15.12):

1. Построить го-

ризонтальный золо-

той эллипс m₁;

2. Выделить на

линии эллипса необ-

родимое и достаточ-

ное число равномер-

но расположенных то-

чек;

3. Соединить эти

Точки с фокусами F¹₁

и F²₁ и провести бис-

сектрисы образовав-

шихся углов, кото-

рые являются нор-

лями эллипса в вы-бранных точках;

4 Построить эволюту е₁ эллипса как линию, огибающую последовательные по-ложения его нормалей l₁. Вершины N₁, E₁, M₁ L₁ эволюты е₁ строятся в пересечении с осями А₁В₁ и С₁D₁ прямых, проходящих че-

рез вершины 1, 2,3, и 4 габаритного прямо-

угольника перпендикулярно к сторонам ро-

мба А₁ С₁ В₁ D₁;

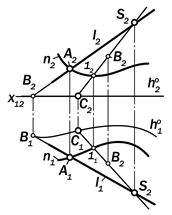
Рис. 15.14. Графическая модель опре-делителя конической поверхности

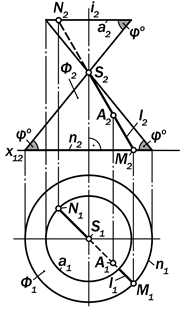
Рис. 15.15. Графическая модель

поверхности прямого кругового конуса

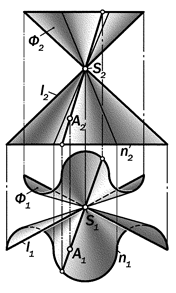
Рис. 15.16. Графическая модель поверх-

ности конуса произвольного вида

5. Так как по условию все образующие

наклонены к плоскости кривизны золотого эллипса под постоянным углом j°, значе-ние которого дано по условию при вершине D₁ линейного угла А₁ D₁ C₁, то для постро-ения фронтальной и профильной проекции золотого торса следует (рис.15.13):

5.1. приняв горизонтальные проекции образующих торса за прилежащие катеты прямоугольных треугольников, конгруэнт-ных треугольнику А₁ О₁ D₁, определить графически значения их противолежащих катетов h5, h6, приходящихся на величины горизонтальных проекций образующих от точек на эллипсе до точек типа 5₁ , 6₁. Эти точки определяют горизонтальную проек-цию «гребня n» золотого торса как линии, состоящей из точек пересечения равнона-клонённых образующих, которые зеркально симметричны относительно фронтальной плоскости треугольника АSВ;

5.2. отложив по линиям связи с точками типа 5₁,6₁ от А₂О₂ значения h5, h6, полу-чить их фронтальные проекции 5₂, 6_2, кото-рые определяют фронтальную проекцию гребня n.

5.3. по горизонтальной и фронтальной проекции гребня n построить его профиль-ную проекцию.

6. Если на фронтальных проекциях об-разующих, продолженных за гребень n, по-строить в проекционной связи с горизон-тальными проекциями точек их касания к эволюте эллипса, фронтальные проекции этих точек, то они определят пространст-венное ребро возврата поверхности золото-го торса как пространственный аналог эволюты его основания – золотого эллипса.

Вывод: Движение образующей прямой линии, сохраняющей постоянный угол на-клона к плоскости кривизны направляю-щей плоской кривой является эффектив-ным средством формообразования широ-кого класса торсов с интересными конст-руктивно-композиционными свойствами.

15.3.4. Изобразительные свойства ортогональных проекций конической поверхности

(рис.15.14 – 15.16)

Определитель конической пове-рхности представляет собой геомет-рическую конструкцию, состоящую из одной прямолинейной образующей l, проходящей через неподвижную точку S и пересекающей криволинейную на-правляющую m.

ф =(l Î S) ´ m.

Графическая модель этой геомет-рической конструкции (рис. 15.14) явля-

ется обратимым изображением, одно-

значно задающим определяемую ко-ническую поверхность. Это означает, что она создаёт на чертеже необходи-мые и достаточные условия для графи-ческого моделирования любых инци-денций данной поверхности. Для того, чтобы по одной проекции D₁ точки D построить её вторую проекцию, необ-ходимо изобразить проходящую через неё горизонтальную проекцию образу-ющей, которая пересекает проекцию m₁ направляющей m в точке 1_1, по ней по-строить фронтальную проекцию этой образующей, на которой, в проекцион-ной связи с D_1, определить искомую проекция D₂ точки D.

Для построения горизонтального следа h°₁ этой поверхности по её опре-делителю следует изобразить необхо-димое и достаточное количество её об-разующих, построить их горизонталь-ные следы и, соединив их плавной кри-вой линией, получить искомый горизон-тальный след. И т. д.

Наиболее распространённым ви-дом конической поверхности является поверхность прямого кругового конуса или конуса вращения (рис.15.15).

Эта поверхность является частным случаем поверхности одинакового ската так как образующая l, пересекающая ось вращения і в точке S, сохраняет постоянный угол j° её наклона к плос-кости кривизны окружности основания m как траектории вращения её точки М.

Утверждение 15.3. Если ось вра-щения поверхности прямого кругового конуса занимает горизонтально-прое-цирующее положение, то очерком го-ризонтальной проекции этой поверх-ности является окружность m₁ как траектория вращения конца М обра-зующей l, а очерком её фронтальной проекции являются два подобных и симметрично расположенных равно-бедренных треугольника, изображаю-щих её нижнюю и верхнюю полы.

Позиционно линия основания m₁ является её горизонтальным следом в случае, если плоскость её кривизны со-впадает с горизонтальной плоскостью проекций.

Поверхность прямого кругового ко-нуса примечательна тем, что линии её пересечения плоскостями различного

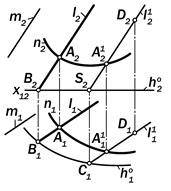
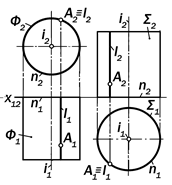
Рис. 15.17. Графическая модель опреде-лителя цилиндрической поверхности

Рис.15.18. Графические модели

проецирующих цилиндрических

поверхностей

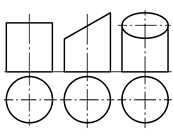
Рис.15.19. Различные виды очерков горизонтально-проецирующих

цилиндрических поверхностей

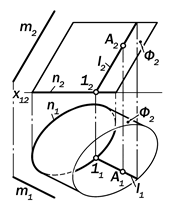
Рис.15.20. Графическая модель

произвольной цилиндрической

поверхности

положения по отношению к её образую-

щим являются алгебраическими кривы-ми линиями 2-го порядка (см.глава 13, п.13.2) или кониками. Так как соответст-венные точки этих линий коллинейны, т.е., лежат на прямых, пересекающихся в одной точке, – вершине S, то их со-ответственные хорды будут при про-должении пересекаться в точках, лежа-щих на рёбрах тех двугранных углов, в гранях которых лежат соответственные коники.

Другими словами, все плоские кри-вые линии на поверхности прямого кру-гового конуса являются в проективном смысле взаимно гомологичными фигу-рами, а в проекционном – центральны-ми проекциями друг друга.

Если направляющей является кри-вая линия m произвольного вида, то об-разующая линия l, проходя через точку S и пересекая эту направляющую в ра-зличных точках, образует коническуюповерхность произвольного вида (рис. 15.16).

15.1.5.Изобразительные свойства ортогональных проекций цилиндрической поверхности

(рис.15.17 -15.19)

Определитель цилиндрической по-

верхности представляет собой геоме-трическую конструкцию, состоящую из одной прямолинейной образующей l, которая параллельна некоторому на-

правлению n и пересекает криволиней-ную направляющую m.

Ф =(l || n) ´ m.

Графическая модель этого опреде-лителя является обратимым изображе-нием, которое однозначно задаёт изоб-ражаемую поверхность. Это значит, что на этом простейшем чертеже цилиндри-ческой поверхности можно решать все позиционные задачи на принадлежно-сть (рис.15.17).

Наиболее распространённым ви-дом цилиндрической поверхности явля-ется поверхность прямого круговогоцилиндра (рис.15.18). У такой поверх-ности направляющей линией является окружность, а все её образующие пер-пендикулярны к плоскости её кривизны. Если эта плоскость совпадает с той или

иной плоскостью проекций или являет-ся той или иной плоскостью уровня, то

её образующие совпадают с направле-нием ортогонального проецирования и

вся поверхность становится проецирую-щей. Это определяет изобразительные свойства её ортогональных проекций.

Утверждение 15.4. Если поверх-ность прямого кругового цилиндра за-нимает в пространстве то или иное проецирующее положение, то очерком одной из её проекций является окруж-ность, обладающая собирательным свойством, а очерком второй – прямо-угольник, трапеция или составной фи-гура с двумя прямыми углами и двумя параллельными противоположными сторонами, которые сопрягаются ду-гой эллипса (рис.15.19).

Поверхность прямого кругового ци-линдра примечательна тем, что в резу-льтате её пересечения плоскостями ра-зличного положения получаются только эллипсы с различными отношениями длин их осей, а их точки лежат на па-раллельных образующих, проходящих через соответственные точки окружно-сти её основания. Это означает, что об-разующие, подобно проецирующим лу-чам, устанавливают между точками ос-нования и любого плоского сечения ро-дственное соответствие, центр которого удален в бесконечность по направле-нию образующих, а осью родства явля-ется след плоскости сечения поверхно-сти на плоскости её основания

Если направляющая линия не явля-

ется окружностью, а образующая не об-разует прямой угол с плоскостью её кривизны и параллельна произвольно расположенной прямой n, то образуется цилиндрическая поверхность, о харак-тере которой судят по виду её нормаль-ного сечения (см. Определение 15.3), Для этого необходимо решить позици-онную задачу на определение вида линии пересечения данной поверхнос-

ти плоскостью, перпендикулярной к её образующим.

На рис.15.20. изображена поверх-ность эллиптического цилиндра с па-раллельными горизонтальными эллип-тическими основаниями. Поэтому очер-ком её фронтальной проекции являетс-ся параллелограмм, а в состав очерка горизонтальной проекции входят две параллельные прямые, сопрягающие две дуги эллипсов её оснований.

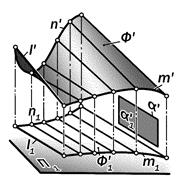
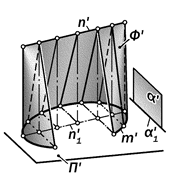
Рис.15.21. Геометрическая модель

поверхности цилиндроида

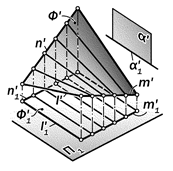
Рис.1522. Геометрическая модель

поверхности коноида

Рис.15.23. Геометрическая модель

поверхности гиперболического

параболоида

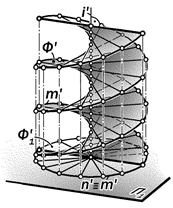
Рис.15.24. Геометрическая модель поверхности прямого винтового

цилиндроида

Если направление проецирования поменять с ортогонального на косоуго-льное, параллельное образующим эл-липтического цилиндра, тогда его по-верхность станет проецирующей, а ли-ния m₁ горизонтальной проекции её ос-нования станет обладать собиратель-ным свойством.

15.1.6. Конструктивные свойства прямолинейчатых поверхностей с двумя направляющими линиями и плоскостью параллелизма

(рис. 15.21-15.24)

Определение 15.6. Системы по-следовательных положений прямоли-нейной образующей, перемещающейся по двум направляющим линиям парал-лельно некоторой плоскости, называ-ются поверхностями с плоскостью параллелизма или поверхностями Ка-талана.

Таким образом, в определитель по-верхности Каталана входит прямоли-нейная образующая l, две направляю-щие m и n и плоскость параллелизма a:

Ф =(l ´ m,n) || a.

В зависимости от того, какой вид приобретают направляющие линии m,n, различаются следующие виды поверх-ностей Каталана:

1. если обе направляющие линии – плоские или пространственные кривые, то получаемая поверхность называется цилиндроидом (рис.15. 21);

2. если одна из направляющих ли-ний кривая, а вторая – прямая, то полу-чаемая поверхность называется конои-дом (рис.15. 22);

3. если обе направляющие линии –скрещивающиеся прямые, то получае-мая поверхность называется гипербо-лическим параболоидом (рис15. 23).

Совершенно очевидно, что видов поверхностей Каталана столько, сколь-ко будет принято для их образования видов направляющих линий в их разли-чных сочетаниях.

В частности, если в качестве напра-вляющей линии принимать цилиндри-ческую или коническую винтовую, то с её участием образуются винтовые по-верхности Каталана.

Определение 15.7. Система по-следовательных положений прямоли-нейной образующей, перемещающейся по двум соосным конгруэнтным цилин-дрическим винтовым линиям паралле-льно плоскости, перпендикулярной к их оси, называется поверхностью прямо-го винтового цилиндроида (рис.15. 24).

Структура прямых винтовых цилин-дроидов лежит в основе конструирова-ния пандусов многоэтажных гаражей.

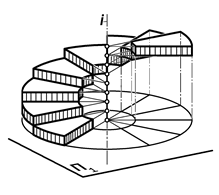
Определение 15.8. Система по-следовательных положений прямоли-нейной образующей, перемещающейся по цилиндрической или конической вин-товой линии и перпендикулярной к её оси, называется прямым винтовым ко-ноидом (рис.15.25).

Структура прямых винтовых конои-дов лежит в основе конструирования винтовых лестниц.

Рис. 15.25. Геометрическая модель прямого

винтового коноида

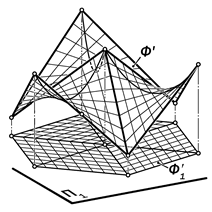
Наиболее распространёнными в архитектуре являются поверхности ги-перболических параболоидов или ги-паров как полностью прямолинейчатых (рис. 15.26).

Рис.15.26. Примеры применения гипаров в

архитектуре

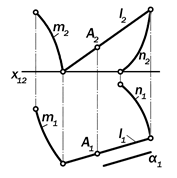
Рис.15.27. Графическая модель опре-делителя поверхности цилиндроида

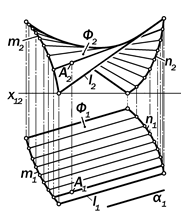
Рис.15.28. Графическая модель

поверхности цилиндроида

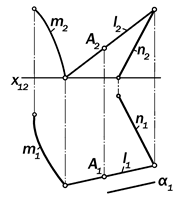
Рис.15.29. Графическая модель

определителя поверхности коноида

15.1.7. Изобразительные свойства ортогональных проекций