Торсовых поверхностей

Определение 15.1. Система по-парно пересекающихся прямолинейных

образующих l, касательных к прост-ранственной направляющей кривой линии m, называется торсовой повер-хностью Ф (рис. 15.1).

Так как образующая I касательна к направляющей m, т.е., I º t, то она де-лится точкой касания А на две полука-сательные t¹ и t², которые, перемеща-ясь, образуют две полы торсовой по-верхности. При этом направляющая пространственная кривая линия m при-обретает название её ребра возврата.

В случае, если роль ребра возвра-та станет играть пространственная ло-маная линия, то кривая торсовая по-верхность преобразуется в поверхность гранного торса.

Если ребро возврата преобразует-ся в точку S º m, то образующие-каса-тельные, пересекаясь в ней, формиру-ют трёхпараметрическую связку пря-мых линий, ибо они потенциально сое-диняют её со всеми точками 3-х-мер-ного эвклидова пространства.

Если в такую связку «погрузить» произвольную линию n, то она «выде-лит» из неё двупараметрическое мно-жество образующих I как некоторую ко-ническую поверхность Ф (рис. 15.2).

Определение 15.2. Двупарамет-рическая система прямых линий I, пе-ресекающих произвольную кривую ли-нию n и проходящих через произволь-ную точку S пространства, называ-ется конической поверхностью Ф.

Так как видов направляющей линии n бесчисленное множество, то каждой из них соответствует своя коническая поверхность. В частности, если линией n будет окружность, а перпендикуляр, опущенный из точки S на плоскость её кривизны, пройдет через её центр, то

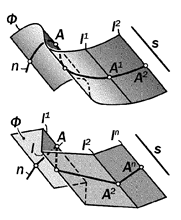
Рис. 15.4. Геометрические модели

цилиндрической поверхности и её

многогранного прототипа

(призматической поверхности)

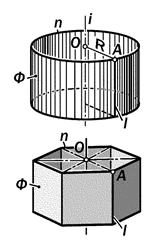
Рис. 15.5. Геометрические модели

поверхностей прямого кругового цилиндра и правильной 6-гранной призмы

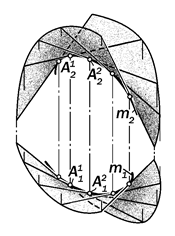
Рис.15.6. Графическая модель

произвольного торса

прямые линии l образуют поверхность

прямого кругового конуса (рис.15.3), если эллипс,- то поверхность эллипти-ческого, если парабола,- то параболи-ческого и т.п., конуса как части прост-ранства, ограниченного такой поверх-ностью.

Так как перечисленные линии явля-ются закономерными плоскими кривы-ми, то их можно рассматривать как ре-зультаты пересечения образуемых ко-нических поверхностей плоскостями их кривизны. В этом случае они становят-ся основаниями этих поверхностей, а точка S – их вершиной.

Длина перпендикуляра, опущенно-го из вершины конической поверхности на плоскость её основания, называется её высотой.

Если в окружность основания пря-мого кругового конуса вписать тот или иной правильный многоугольник, то его поверхность преобразуется в поверх-ность правильной пирамиды, гранями которой будут конгруэнтные равнобед-ренные треугольники.

Пирамидальная поверхность, также как и коническая, является двупольной.

Если представить, что вершина ко-нической поверхности удаляется в бес-конечность, а направляющая n остаёт-ся неподвижной и неизменной, то эта поверхность преобразовывается в ци-линдрическую, образующие l которой, стремясь в бесконечно-удалённую вер-шину, оказываются параллельными.

Определение 15.3. Двупараме-трическая система прямых линий l, параллельных заданному направлению s и пересекающих заданную произволь-ную кривую линию n, называется ци-линдрической поверхностью Ф (рис. 15.5).

Так как видов направляющей кривой линии n бесчисленное множество, то каждой из них соответствует своя ци-линдрическая поверхность. В частнос-ти, если линией n является окружно-сть, а все образующие l перпендику-лярны к плоскости её кривизны, то они формируют поверхность прямого кру-гового цилиндра как часть простран-ства, ограниченного этой поверхностью.

Если направляющую окружность поверхности прямого кругового цилинд-

ра принять за её основание, то позици-

онно она станет фигурой нормального

сечения данной поверхности.

По виду нормального сечения судят о виде поверхности цилиндра. Если оно имеет вид эллипса, то цилиндр эллип-тический, если гипербола, то гипербо-лический и т.п., а если произвольная линия, то получается цилиндрическая поверхность произвольного вида.

Если в окружность основания пове-рхности прямого кругового цилиндра вписать правильный многоугольник и принять его за направляющую линию, то образуется многогранный прототип цилиндрической поверхности – призма-тическая поверхность, гранями кото-рой будут конгруэнтные прямоугольни-ки.

Утверждение 15.1. Так как прямо-линейные образующие цилиндрических и конических поверхностей инциден-тны соответственно несобственной и собственной вершинам, которые ко-нцептуально являются вырожденны-ми рёбрами возврата некоторых тор-сов, то эти поверхности относятся к классу торсовых.

15.1.2. Изобразительные свойства ортогональных проекций торсовой поверхности

Так как прямолинейные образую-щие торсовой поверхности касательны к пространственной направляющей кри-вой, то для построения её ортогональ-ных проекций необходимо графически смоделировать отношение их касате-льности. (см.Главу 5, стр. 55-58).

Конструктивно касательное положе-ние прямой линии по отношению к кривой является её крайним секущим, когда точки их пересечения сливаются в одну двойную точку их касания. Орто-гональное проецирование так располо-женных линий порождает в пространс-тве плоскость, которая проецирует пря-мую линию и касается к цилиндриче-ской поверхности, которая проецирует кривую линию. Их пересечение с плос-костью проекций показывает, что проек-ция прямой линии касательна к проек-ции кривой линии в проекции точки их касания. Отсюда следует

Утверждение 15.2. Если в прост-ранстве прямая линия касательна к

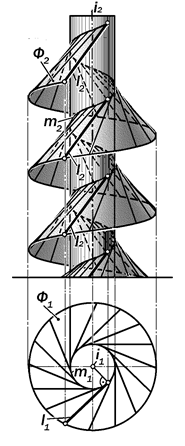
Рис.15.7. Графическая модель развер-тываемого геликоида

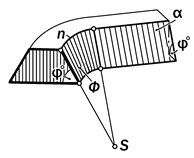
Рис.15.8. Геометрическая модель

поверхности откоса насыпи от горизонтальной составной бровки

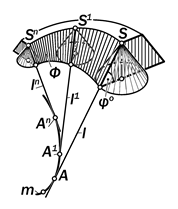
Рис.15.9. Геометрическая модель поверхности откоса насыпи от пространственной бровки

плоской или пространственной кри-вой, то одноименные проекции этих линий касательны в соответствую-щих проекциях точки их касания.

Иными словами, отношение касате-льности инвариантно или устойчиво в процессе преобразования изображае-мых касающихся линий в их соответст-вующие ортогональные проекции.

Соблюдение этого обстоятельства позволяет правильно строить ортогона-льные проекции произвольной торсовой поверхности (рис.15.6).

Так как видов пространственных кривых достаточно много, то каждой из них соответствует своя торсовая повер-хность. К примеру, если в качестве ре-бра возврата принять цилиндрическую винтовую линию, то образующая l, пе-ремещаясь касательно к ней, своими последовательными положениями об-разует поверхность развёртываемогогеликоида (рис.15.7).

Определение 15.4. Система по-парно пересекающихся прямолиней-ных образующих, касающихся к цилин-дрической винтовой линии, называет-ся поверхностью развертываемого ге-ликоида.

Определение 15.5. Геликоидами называются винтовые поверхности, в образовании которых в качестве на-правляющих применяются винтовые линии.

Поверхность развертываемого ге-ликоида в частном случае может быть поверхностью одинакового ската, при-меняемого для образования откосов на-сыпей и выемок в земном рельефе при прокладке шоссейных и железных до-рог. Линии наибольшего уклона этих от-косов должны быть равнонаклонены к горизонтальной плоскости. Если бров-кой откоса насыпи или выемки является прямая линия, то поверхность откоса является плоскостью; если орямоли-нейная бровка переходит в дугу гори-зонтальной гладкой кривой, то от неё откос приобретает форму конической поверхности, сопряженной с плоским откосом по линии её наибольшего ук--лона (рис. 15.8), а если, на вираже, эта линия становится пространственной, то идущий от неё откос приобретает фор-му поверхности торса (рис.15.9). Для её образования применяют поверхность

прямого кругового конуса как частного случая торса, все образующие которой равнонаклонены к плоскости его осно-вания. Поверхность, огибающая после-довательные положения такого конуса, вершина которого перемещается по пространственной бровке дороги, явля-ется поверхностью искомого откоса, ли-нии наибольшего уклона которого рав-нонаклонены к горизонтальной плоско-сти и при продолжении касательны к некоторому пространственному ребру возврата m (см. рис.15.9).

15.3.3. Изобразительные свойства