Загальне рівняння площини та його частинні випадки

Рівняння (1), до якого зводяться рівняння площини в усіх розглянутих випадках, називають загальним рівнянням площини. Розглянемо особливості розташування площини відносно системи координат у випадках, коли деякі з коефіцієнтів дорівнюють нулю. При цьому будемо користуватись наступною лемою.

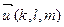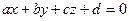Лема. Для того, щоб вектор був паралельним до площини , заданої рівнянням , необхідно та достатньо, щоб виконувалася рівність

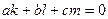. (6)

Доведення. Нехай вектор 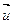паралельний до площини , а також точка 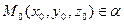є початком вектора 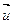. Тоді точка 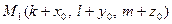, для якої 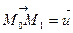, теж належить площині, а її координати задовольняють рівняння площини. Тому

.

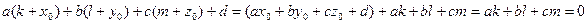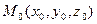Навпаки, нехай виконується рівність Візьмемо на площині довільну точку та розглянемо точку 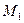таку, що 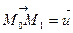. Тоді точка 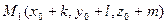належать площині , в чому легко переконатися, підставивши її координати в рівняння площини. Отже, вектор 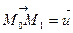паралельний площині .

Перейдемо до розгляду частинних випадків рівняння (1).

1). Нехай , тобто рівняння площини має вигляд 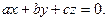Очевидно, що 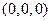– розв’язок рівняння. Тому площина проходить через початок координат.

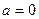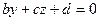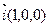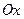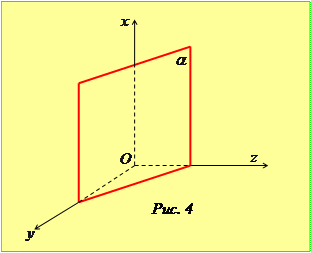
2). Нехай . Тоді рівняння площини набуває виду . Розглянемо вектор , паралельний до осі . Згідно з доведеною лемою він паралельний до площини , тому у цьому випадку площина паралельна до осі 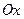(рис. 4). Аналогічні висновки робимо при 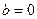та 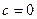. Тобто площина, задана рівнянням 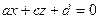, паралельна до осі 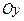, а площина, задана рівнянням 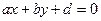, паралельна до осі 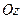. Якщ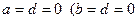о або 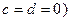, то площина проходить через вісь 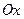(відповідно через вісь 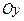або вісь ).

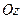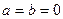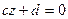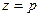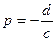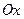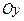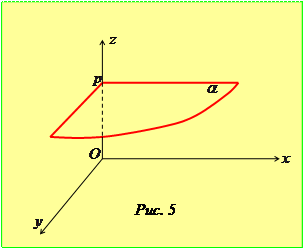
3). У випадку, коли , рівняння площини набуває вигляду або , де . Тоді площина , будучи паралельною до осей та , буде також паралельною до площини 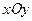(рис. 5). При 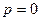рівняння 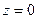є рівнянням площини 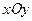. Аналогічно, якщо 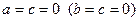, то рівняння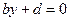 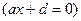задає площину, яка паралельна до площини 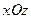(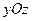). Рівняння 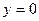та 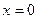є рівняннями площин 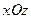та 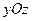відповідно.