Обтекание тел при малых возмущениях

Если плоский равномерный поток газа подвергается малым возмущениям , то при направлении оси вдоль вектора можно записать

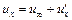; , (12.81)

где 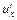, – проекции скорости возмущенного движения.

Если пренебречь квадратами и произведениями этих величин, то в линейном приближении

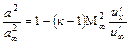; (12.82)

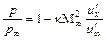; (12.83)

; (12.84)

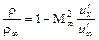, (12.85)

где 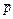– коэффициент давления.

Составляющая скорости возмущения 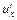определяется через потенциал малого возмущения

, (12.86)

причем

Потенциал скорости при малых возмущениях удовлетворяет уравнению

(12.87)

Рис. 12.6. Распространение малых возмущений в дозвуковом (а), звуковом (б) и сверхзвуковом (в) потоках газа

Если в равномерном потоке газа точка А (рис. 12.6) является источником малых возмущений (малых изменений плотности и давления), то эти возмущения в виде слабой волны распространяются в потоке. В зависимости от скорости потока фронты волн возмущения могут занимать одно из положений, показанных на рис. 12.6. В дозвуковом течении (рис. 12.6, а) фронты волн возмущения представляют собой окружности радиусом 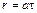, смещаемые вниз по течению на расстояние , где – время с момента возникновения возмущения.

При сверхзвуковой скорости потока газа волны возмущений также имеют вид окружностей, но в силу условия 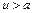область их распространения ограничивается прямыми AM и AN (для осесимметричного потока – поверхностью конуса), называемыми линиями возмущения, или линиями Маха. Эти прямые образуют с вектором скорости угол Маха, определяемый формулой

. (12.88)

Течение при дозвуковых скоростях. При (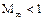) замена переменных 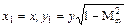приводит уравнение для потенциала скорости к уравнению Лапласа , т.е. к уравнению, которому удовлетворяет потенциал скорости несжимаемой жидкости. Поэтому при обтекании дозвуковым потоком газа тонкого профиля с малым углом атаки задача приводится к задаче обтекания профиля несжимаемой жидкостью. Формулы пересчета согласно теории Прандтля - Глауэрта имеют вид:

для коэффициента давления

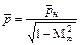; (12.89)

для коэффициента подъемной силы

, (12.90)

где индексом «н» отмечены параметры потока несжимаемой жидкости.

Течение при сверхзвуковых скоростях. Линеаризованное уравнение потенциала скорости заменой переменных 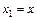, приводится к уравнению гиперболического типа

, (12.91)

имеющему общее решение в переменных , :

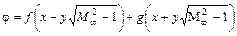, (12.92)

где , – произвольные функции.

Два семейства прямых, совпадающих с линиями возмущения линеаризованного потока и описываемых формулой , являются характеристиками уравнения (12.91).

Сверхзвуковое обтекание малого угла, образованного плоскими стенками (рис. 12.7). При таком течении из вершины угла выходит характеристика первого семейства, которая делит область течения на две части: невозмущенную и возмущенную. При обтекании выпуклого угла (рис. 12.7, а) поток ускоряется, а при обтекании вогнутого – замедляется (рис. 12.7, б).

Обтекание тонкого профиля с заостренными кромками. Задача может быть приближенно решена на основе линеаризованной теории. При этом плавный контур профиля заменяют ломаным (рис. 12.8) и последовательно решают задачу об изменении параметров потока при переходе через каждую линию возмущения, выходящую из точек излома. В результате получают следующие формулы для коэффициента давления:

для верхней поверхности, заданной уравнением ,

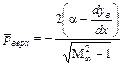; (12.93)

для нижней поверхности, заданной уравнением ,

, (12.94)

где – угол атаки (рис. 12.8).

Рис. 12.7. Схемы обтекания сверхзвуковым потоком малого угла:

а – ускорение потока; б – торможение потока

Рис. 12.8. Расчетная схема обтекания тонкого профиля

линеаризованным сверхзвуковым потоком газа

Коэффициент подъемной силы

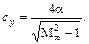(12.95)

Коэффициент волнового сопротивления

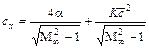, (12.96)

где 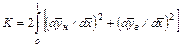; ; 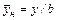; , причем – максимальная толщина профиля; – его хорда.

Момент сил давления относительно передней кромки

, (12.97)

где – коэффициент момента,

, (12.98)

здесь 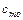– коэффициент момента при нулевом угле атаки,

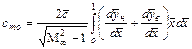; (12.99)

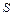– площадь, равная .