Возможность и вероятность

Когда имеется информация о появлении событий в форме измеренных частот элементарных событий, полученная мера неопределенности естественным образом удовлетворяет аксиоме аддитивности

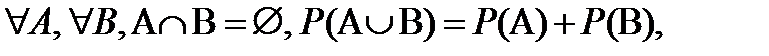(7.19)

т.е. становится вероятностной мерой, [97] которая, конечно, является монотонной в смысле условия (7.2). Формула (7.19) – вероятностный эквивалент аксиом (7.6) и (7.11).

Условие, эквивалентное условиям (7.9) и (7.14), для конечного случая записывается в виде

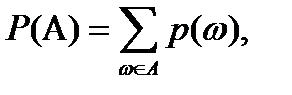(7.20)

где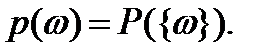

Условие нормировки 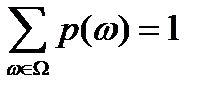является аналогом условия (7.10). Общая черта вероятностных мер, мер возможности и необходимости заключается в том, что все они могут характеризоваться некоторыми распределениями на элементах универсального множества.

Здесь аналогом соотношений (7.8) и (7.15) является хорошо известное соотношение

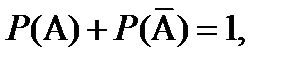(7.21)

в то время, как из (7.8) и (7.15), следуют лишь неравенства

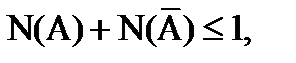(7.22)

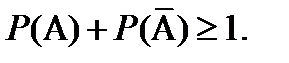(7.23)

Из этих соотношений видно одно из главных различий между возможностью и вероятностью. Вероятность некоторого события полностью определяет вероятность противоположного события. Возможность (или необходимость) некоторого события и возможность (необходимость) противоположного ему события связаны слабее; в частности, для того, чтобы охарактеризовать неопределенность по отношению к событию 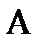, требуется два числа 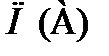и 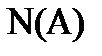, удовлетворяющие условию (7.17) или (7.18).

Когда моделируется субъективное суждение, кажется естественным стремление не устанавливатьжесткой связи между показателями, свидетельствующими в пользу некоторого события (степень необходимости), и показателями, свидетельствующими против него (степень возможности). В этой ситуации понятие вероятности оказывается менее гибким, чем понятие меры возможности.

Даже когда сохраняется требование аддитивности, можно построить меры возможности и необходимости, если не требовать дополнительно, чтобы значения вероятностей (распределение p) относились к элементарным событиям. Точнее, пусть непустые, попарно различные подмножества (предполагаемого конечным), с соответствующими значениями вероятности 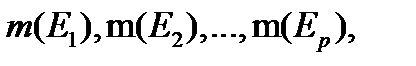такими, что

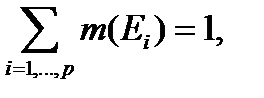(7.24)

и 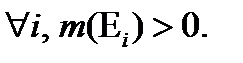(7.25)

Величина 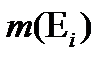понимается как значение вероятности совокупности элементарных событий, составляющих 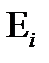, причем здесь не оговаривается распределение величины

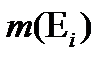по элементарным событиям. Подмножества 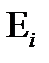называются «фокальными элементами» и могут отражать неточность наблюдений. В этой ситуации вероятность события 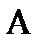можно охарактеризовать лишь неточно как величину, содержащуюся в интервале 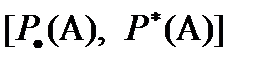с границами

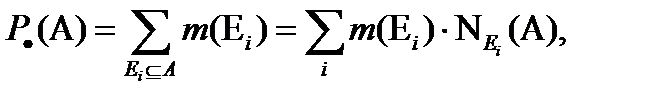(7.26)

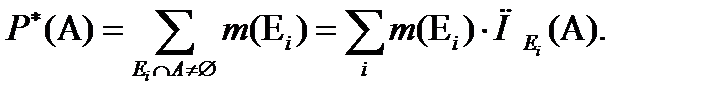(7.27)

Значение вычисляется по всем фокальным элементам, которые делают необходимым появление события 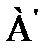(или влекут за собой событие 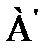). Значение получается при рассмотрении всех фокальных элементов, которые делают возможным появление события 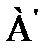. Отметим, что имеется отношение двойственности между 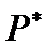и :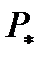

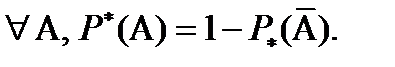(7.28)

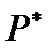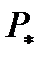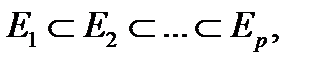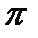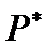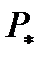Доказано (Шейфер [24]), что функция (соответственно ) удовлетворяют аксиоме (7.6) (соответственно (7.11)), т.е. является мерой возможности (соответственно необходимости) тогда и только тогда, когда фокальные элементы образуют последовательность вложенных множеств. А именно если то функция распределения возможностей , связанная с и , определяется в виде

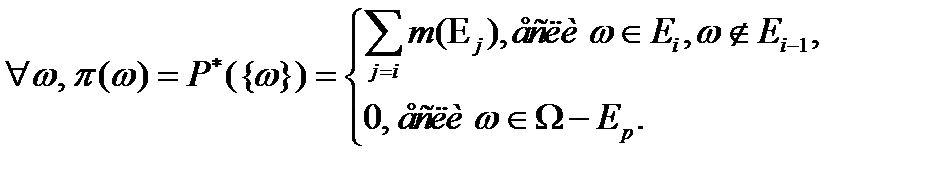(7.29)

Ясно, что если, наоборот, фокальные элементы являются элементарными (а значит, несовместными) событиями, то т.е. снова возвращаемся к вероятностной мере.

Если схематично представить базу знаний с помощью множества фокальных элементов, которые являются составляющими «значение» в наборе, описывающем информационную единицу, то легко понять, что вероятностные меры [17], естественным образом синтезируют базу точных и дифференцированных знаний, тогда как меры возможности [97], суть отражение неточных, но связных (т.е. подтверждающих друг друга) знаний. Отметим, что функции возможности в этом смысле более естественны для представления чувства неуверенности: от субъекта не ждут слишком точной информации, но желают услышать по возможности наиболее связную речь. Зато точные, но флуктуирующие, данные чаще всего получают из наблюдений физического явления.

Несомненно, в базе знаний будет содержаться информация, которая в общем случае не сведется ни к точной, ни к полностью согласованной информации. Вероятность, с одной стороны, и пара «возможность-необходимость» - с другой соответствуют двум крайним, а значит, идеальным ситуациям.

Формулы (7.26) и (7.27) позволяют считать, что функция распределения возможностей определяет класс вероятностных мер Р, такой, что

(7.30)

Это позволяет строго определить понятие математического ожидания в рамках мер возможности. Если f- функция, определенная на и принимающая значения из множества действительных чисел , то верхние и нижние математические ожидания f, обозначаемые 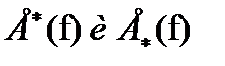соответственно, определяются с помощью интегралов Лебега-Стилтьеса (Демпстер [23]):

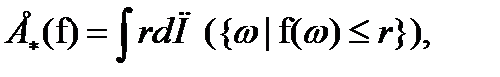(7.31)

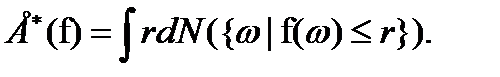(7.32)

Названия верхних и нижних математических ожиданий оправдываются тождествами

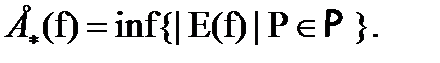(7.33)

Эти соотношения были получены Демпстером для случая, когда множество

конечно; более общий случай описан в данной работе.