Теоретична частина. Через різноманітні неконтрольовані дії результати виміру макроскопічної величини мають статистичний характер

Через різноманітні неконтрольовані дії результати виміру макроскопічної величини мають статистичний характер. В основному це відноситься до статистичності процесу виміру. Можливі флуктуації і самої вимірюваної величини, проте вони можуть бути зроблені як завгодно малими. Тому можна вважати, що сама по собі вимірювана величина (наприклад, маса якого-небудь тіла, довжина стержня і т. д.) має деяке цілком визначене значення, тоді як результати вимірів флуктуюють через недосконалість вимірювальних приладів, недостатньої їх ізоляції від зовнішніх умов, що змінюються, і так далі. Чисельні значення результатів вимірів зазвичай розподілені по деякому безперервному ймовірному закону, найчастіше за законом Гауса.

Зовсім по-іншому йде справа з багатьма вимірами в ядерній фізиці. На відміну від макросвіту в мікросвіті флуктуації вимірюваних величин зв'язані, як правило, з самою суттю явищ і тому не можуть бути зроблені як завгодно малими.

Якщо, наприклад, йдеться мова про виміри числа актів радіоактивного розпаду, що стався за якийсь час, то флуктуює сама вимірювана величина, а вимірювальний прилад (лічильник частинок) в першому наближенні можна вважати ідеальним, тобто не схильним до статистичного впливу довколишніх умов. Вимірювана величина (наприклад, число актів радіоактивного розпаду) є вже не безперервною, а дискретною, і найбільш характерним законом розподілу, замість закону Гауса, є закон Пуасона, а інколи біноміальний закон.

Роль статистичного підходу в мікросвіті значно глибша, ніж в макрофізиці. Статистика тут потрібна не лише для обробки результатів вимірів, але і для вивчення самої природи досліджуваних явищ. Наприклад, природа радіоактивності була остаточно встановлена лише після завершення детального статистичного аналізу, який показав, що різні акти розпаду між собою статистично незалежні.

Інший приклад. При дослідженні космічних променів за допомогою камери Вільсона було виявлено, що число частинок, які реєструються при різних послідовних розширеннях камери, розподілене не за законом Пуасона. Це спостереження послужило відправною точкою для відкриття і дослідження злив космічних часток.

Помилки, пов'язані з методикою виміру, називають систематичними. Наприклад, детектори ядерних випромінювань і перелічувальні пристрої мають кінцевий мертвий час 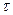. Якщо протягом цього часу виникає декілька імпульсів, то реєструючий пристрій не зможе злічити їх окремо, і, отже, прорахує частину імпульсів. Прорахунки, хоча і пояснюються статистичним характером явищ, але приводять до систематичної помилки, залежної від швидкості рахунку і параметрів системи, призначеної для реєстрації імпульсів.

Розподіл Пуасона. Нехай лічильник опромінюється потоком незалежно наступних один за одним частинок. Попадання тієї або іншої частинки в лічильник є випадковою подією. Тому протягом рівних інтервалів часу через лічильник може пролетіти різна кількість частинок. У цих умовах вірогідність того, що протягом часу t в лічильник попаде 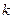частинок, дається відомою формулою Пуасона:

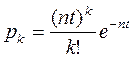, (1)

де n - потік частинок.

Середнє число актів визначається рівністю

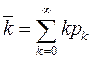(2)

Якщо інтенсивність не залежить від часу, то 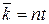, звідки витікає, що інтенсивність п має сенс середнього числа актів, що здійснюються за одиницю часу.

Тоді формулу (1) можна записати у вигляді

(3)

Як видно з формули (3), розподіл Пуасона повністю визначається завданням лише одного параметра - середнього числа актів. Експериментальне визначення 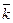є, як правило, основною метою більшої частини вимірів, що проводяться в ядерній фізиці. З формули (3) виходить, що

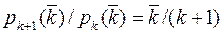(4)

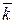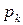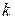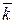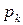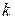
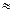
Тому, якщо < < 1, то монотонно спадає із зростанням . Інша картина має місце, коли > 1. В цьому випадку спочатку зростає, досягаючи максимального значення при 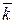, після чого починає монотонно спадати.

Залежність 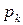від k при різних 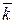зображено на рис. 1. При малих 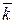спостерігається асиметрія. У міру зростання 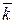максимум стає відносно все більш гострим, а графік - усе більш симетричним відносно 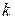= 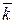. При великому 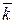графік практично симетричний.

Рис. 1. Залежність від

З формули (3) виходить, що при всякому значенні 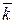можливе здійснення будь-якого числа актів 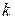. Проте не всі події зустрічаються однаково часто. Якщо величина 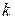близька до 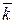, то вірогідність 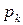велика, інакше - мала. Мірою відхилення випадкової величини 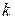від її середнього значення (мірою флуктуації) є дисперсія.

Дисперсією деякої випадкової величини х називається вираз

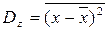(5)

Величину 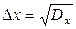називають абсолютною флуктуацією випадкової величини х, а величину 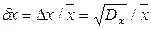- її відносною флуктуацією.

У випадку закону Пуасона дисперсія

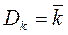(6)

абсолютна флуктуація

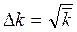(7)

відносна флуктуація

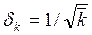(8)

де - середнє число актів.

Співвідношення (6).. (8) відіграють основну роль у всіх доданках закону Пуасона. Їх сенс полягає в наступному. Якщо реєструвати відліки лічильника в дуже великому числі рівних інтервалів, то в більшій частині інтервалів число відліків 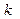відрізнятиметься від не більше ніж на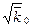

Абсолютна флуктуація (7) збільшується із зростанням , проте відносна похибка 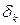(8) зменшується обернено пропорційно до квадратного кореня з числа злічених частинок. Звідси можна знайти число частинок , яке потрібно злічити для досягнення заданої відносної похибки

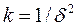(9)

Таким чином, для виміру середнього числа частинок із статистичною похибкию 10 %, потрібно злічити 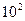частинок. Для того, щоб статистична похибки склала 1 %, потрібно вже 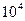частинок і так далі.

Закон Пуасона визначений лише для позитивних значень 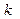. На практиці він часто застосовується в тих випадках, коли потрібно оцінити надійність вимірів і похибки виміряних величин в разі спостереження рідких подій (що відрізняються малою інтенсивністю).

Зв'язок розподілу Пуасона з розподілом Гауса. Вище вже наголошувалося, що у міру зростання розподіл Пуасона стає усе більш симетричним відносно .

Якщо виконується умова

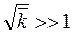(10)

(практично при 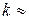20), то досягається повна симетрія. Крім того, відмінність між величинами ймовірності для суміжних або близьких 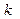виявляється дуже малим. Наприклад, легко перевірити, що при = 1000:

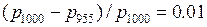(11)

У цих умовах замість імовірності здійснення того або іншого числа відліків можна користуватися вже іншою величиною, а саме, імовірністю р (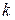) того, що число відліків розміщене в „нескінченно малому" інтервалі від до 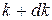. По абсолютній величині інтервал 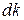може містити декілька одиниць. Проте він малий в порівнянні з тими, що цікавлять нас 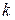, рівними по порядку величини середньому числу відліків . Тим самим дискретний розподіл замінюється безперервним. Кількісний розгляд функції розподілу при виконанні умови (10) приводить до висновку, що дана величина 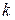розподілена за законом Гауса:

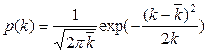(12)

Закон Гауса визначений як для позитивних, так і негативних значень 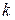. Величина 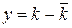, що має сенс відхилення числа відліків 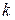від середнього значення, розподілена згідно з законом

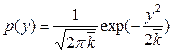(13)

За допомогою (1.13) можна обчислити вірогідність того, що величина 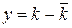поміщена в інтервалі від 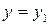до . Шукана імовірність

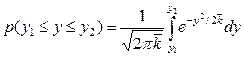(14)

Замінюючи змінну по формулі y = z 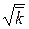, отримаємо

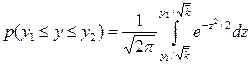(15)

або

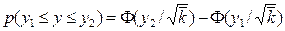, (16)

де 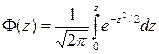(17)

- функція Гауса.

Значення функції Гауса наводяться у всіляких математичних і фізичних довідниках. За допомогою таблиць можна знайти вірогідність того, що відхилення від середнього не перевершує по модулю величини абсолютної похибки ():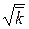

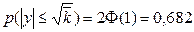(18)

Так само отримуємо

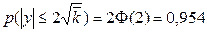(19)

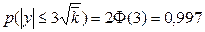(20)

З формул (18)..(20) випливає наступне: якщо реєструвати відліки лічильника у великому числі рівних інтервалів часу, то при виконанні умови (10) в 68,2% випадків число відліків відрізнятиметься від не більше ніж на 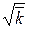, в 95,4% не більше ніж на 2 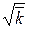і в 99,7% не більше ніж на 3 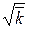і так далі.

Результат виміру числа відліків 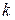наводиться завжди разом зі своєю абсолютною похибкою (зазвичай 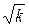), яка є показником статистичної точності вимірів.

Розподіл (12) є частковим випадком розподілу Гауса:

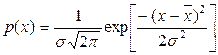(21)

яке залежить від двох параметрів - 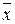і .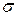

Часто використовується поданні розподілу (21) у функції змінної

u = (х - 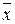) / 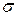, тоді

(22)

У такому записі розподілу Гауса його середнє значення дорівнює нулю, а стандартне відхилення - одиниці.

Розподіл Гауса є хорошим наближенням для опису широкого кола статистичних явищ. У ядерній фізиці розподіл (21) описує, наприклад, розподіл кутів пружнього розсіювання при проходженні зарядженої частинки через речовину, розподіл пробігів важких заряджених частинок в речовині, розподіл імпульсів по амплітудах при реєстрації заряджених частинок напівпровідниковим і сцинтилляційним детекторами і так далі.

Розподіл Гауса широко використовується при аналізі похибок експерименту. Широке використання нормального розподілу в теорії вимірів засноване на доводжуваному в теорії імовірності твердження про те, що випадкова величина, що є сумою дуже великого числа незалежних випадкових величин з практично довільним розподілом, розподілена згідно (21). Останнє твердження означає, що використання нормального закону при описі експериментальних даних можливе в тих випадках, коли досліджувану випадкову величину можна уявити у вигляді суми досить великого числа незалежних елементарних доданків, кожен з яких порівняно мало впливає на суму. Така ситуація часто характерна для складних експериментів. Як приклад можна навести випадок, коли випадкова величина підкоряється рівномірному (рівноімовірному) розподілу: випадкова величина, що є сумою трьох таких величин вже може бути добре апроксимована розподілом Гауса.

Розподіл 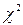(хі-квадрат) знаходить широке використання при перевірці експериментальних даних з деякою апріорною гіпотезою, здобутті довірчих інтервалів для статистичних параметрів, перевірці незалежності змінних і у ряді інших завдань.

Нехай 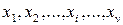- набір ν випадкових величин, кожна з яких розподілена по нормальному закону зі своїм математичним очікуванням 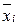і дисперсією 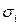. Квадрати нормованих значень 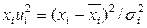через випадковість 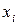- також випадкові величини. Їх сума також є випадковою величиною

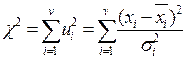(23)

Очевидно, що величина 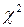завжди позитивна. Параметр ν в (23) називають числом ступенів свободи. Оскільки величини 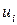нормовані і мають одне і теж середнє значення, рівне нулю, і рівну одиниці дисперсію, то розподіл щільності імовірності випадкової величини 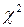повинен залежати лише від одного параметра, а саме від параметра ν. Якщо не всі ν випадкових величин не залежні, то число ступенів свободи, що є параметром в розподілі 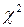, менше ν на число зв'язків. Щільність розподілу імовірності для 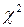задається формулою

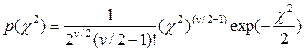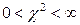, (24)

Середнє значення 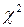дорівнює числу ступенів свободи ν, а дисперсія – 2ν. Для додатків важливий розподіл накопиченої імовірності

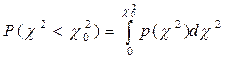(25)

яке важко отримати безпосередньою інтегруванням. У книгах зі статистики наводяться детальні таблиці Р(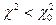) для різних ν.

Перевірка гіпотез про закон розподілу. критерій згоди 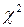. Метою багатьох експериментів є оцінка закону розподілу деякої фізичної величини. У ядерній фізиці це може бути, наприклад, закон кутового розподілу нейтронів, розсіяних на ядрах певного елементу. Точний закон розподілу випадкової величини в експерименті визначити неможливо, оскільки для цього знадобилося б незкінечне число вимірів для отримання генеральної сукупності, а з кінцевого числа вимірів визначається лише кінцева вибірка. З цього відразу випливає важливий висновок про те, що експеримент не доводить правильність гіпотези, а лише дозволяє зробити висновок про несуперечність її з даними експерименту.

Зазвичай перед проведенням досліду вже сформульована одна або декілька апріорних гіпотез, отриманих з теорії або в результаті попередніх експериментів, часто непрямих. Оскільки вимірювана величина випадкова, то, навіть якщо закон її розподілу точно відомий, зважаючи на обмеженість вибірки спостерігатимуться відхилення результатів спостереження від обчислених по розподілу. Виникає питання: чи випадкові спостережувані відхилення виміряних величин від передбачених теорією або є систематичні розбіжності, тобто теорія невірна?

Критерієм згоди називають критерій перевірки гіпотези про передбачуваний розподіл. З його допомогою можна встановити, задавшись так званою довірчою імовірностю, узгоджуються експериментальні дані з апріорною гіпотезою чи ні. Довірча імовірность визначається умовами завдання і зазвичай приймається близькою до одиниці, наприклад 0,95.

На практиці найчастіше використовується критерій згоди 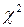. Розглянемо цей критерій. Нехай потрібно перевірити гіпотезу про те, що випадкова величина X розподілена згідно із законом р (х). Розглянемо дослід, в якому отримане n незалежних вимірів X. Розіб'ємо всю область змін X на l інтервалів і підрахуємо кількість 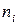виміряних значень X, що попали в кожен з інтервалів. Оскільки теоретичний розподіл р (x) припускається відомим, можна розрахувати теоретичне число значень X в i -му інтервалі 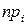, де 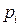- імовірність попадання випадкової величини в i- й інтервал. Якщо експериментальні частоти 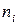сильно відрізняються від теоретичних 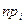гіпотезу про згоду теорії i експерименту слід відкинути. Критерій 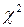дає можливість кількісно виразити цю міру згоди.

Як міра розбіжності між теорією (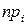) та експериментом (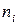) використовують критерій

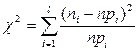(26)

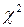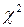Очевидно, що чим менше розрізняються теоретичні та експериментальні частоти, тим менше значення . Оскільки розподіл (26) при прагне до розподілу (див. формулу (24)), цей критерій і названий критерієм згоди 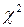. Застосовують його таким чином: розрахувавши значення 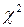і задавшись довірчою імовірністю α (або рівнем статистичної значимості 1− α), знаходять по таблицях значенн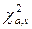я для 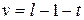, де t - кількість додаткових співвідношень для оцінки параметрів розподілу р(х).

Якщо при даному 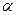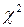< 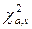-, то теорія та експеримент розходяться, якщо 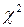< 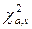- узгоджуються. Також з таблиць можна визначити довірчу імовірність α, при якій <

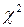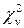
Розглянемо приклад. Проведено n =200 вимірів випадкової величини - в таблиці. 1 приведені значення 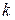і частоти їх появи .

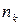Таблиця 1. Експериментальні 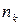і очікувані за Пуасоном 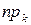частоти.

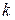
								Всього
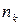
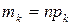
	108,7	66,3	20,2	4,1	0,6	0,07	0,01

Необхідно перевірити гіпотезу про те, що ці дані підкоряються закону Пуассона, тобто що

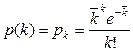
Ми бачимо, що для повного визначення потрібно оцінити параметр 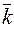. Нехай цією оцінкою буде вибіркове середнє. Середнє 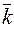обчислимо за формулою

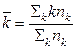(27)

Таким чином

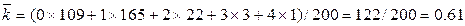
Тоді для очікуваних частот отримуємо вираз

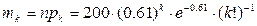
Ці значення приведені в третьому рядку таблиці 1. Оскільки очікувані частоти для 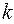> 2 малі, об'єднаємо останні чотири значення 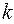і складемо нову таблицю. 2.

Таблиця 2.

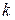
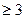
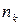
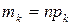
	108,7	66,3	20,2	4,8

Для перевірки гіпотези обчислимо

Для оцінки 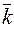ми використовували одне співвідношення (1.27), тому число ступенів свободи рівне 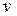=4-1-1=2. Отже, величина 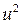має бути розподілена приблизно як .

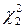З'ясуємо тепер, чи не виявиться величина 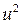настільки великою, що вихідна гіпотеза (розподілу Пуассона) неправдоподібна. З таблиці. 3 знаходимо, що довірчій імовірності р =0,95 (або 5%-му рівню статистичної важливості) відповідає значення 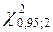= 5,991, тобто величина 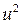повинна знаходитися в межах від 0 до 6,0. Оскільки значення 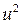потрапляє в цей незначний інтервал, гіпотеза, що перевіряється, приймається.

З іншого боку, якби ми отримали 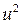=6,1 або більше, то повинні були б вважати його значимим, оскільки, якщо гіпотеза вірна, то лише в 5 випадках з 100 величина 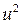набуватиме настільки великих значень.