 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие устойчивости по Ляпунову
|
|
Рассмотрим систему дифференциальных уравнений
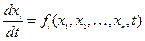 . (1)
. (1)
Решение 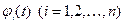 системы (1), удовлетворяющее начальным условиям
системы (1), удовлетворяющее начальным условиям 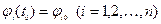 , называется устойчивым по Ляпунову, если для любого
, называется устойчивым по Ляпунову, если для любого 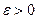 существует
существует 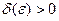 такое, что для всякого решения
такое, что для всякого решения 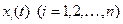 системы (1), начальные значения которого удовлетворяют условиям
системы (1), начальные значения которого удовлетворяют условиям
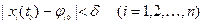 , (2)
, (2)
имеет место неравенство
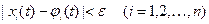 (3)
(3)
для всех 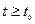 .
.
Если при сколь угодно малом  хотя бы для одного решения
хотя бы для одного решения 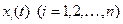 неравенство (3) не выполняется, то решение
неравенство (3) не выполняется, то решение  называется неустойчивым.
называется неустойчивым.
Если кроме выполнения неравенства (3) при условии (2) выполняется также условие
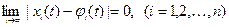 , (4)
, (4)
то решение 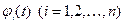 называют асимптотически устойчивым.
называют асимптотически устойчивым.
4.2. Устойчивость по первому приближению
Пусть имеем систему дифференциальных уравнений
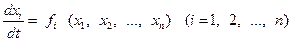 (1)
(1)
и пусть x i 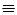 0 (i= 1, 2, …, n) есть точка покоя системы (1), т.е.
0 (i= 1, 2, …, n) есть точка покоя системы (1), т.е.
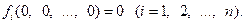
Будем предполагать, что функции fI (x1, x2, …, x n) дифференцируемы вначале координат достаточное число раз.
Разложим функции fi по формуле Тейлора по x-ам в окрестности начала координат. Получим
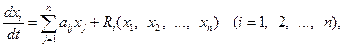 (2)
(2)
где 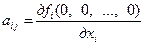 , а
, а 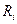 – члены второго порядка малости относительно x1, x2, …, xn.
– члены второго порядка малости относительно x1, x2, …, xn.
Вместо точки покоя системы (1) исследуем на устойчивость ту же точку покоя линейной системы
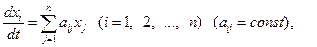 (3)
(3)
называемую системой уравнений первого приближения для системы (1). В этом и состоит метод исследования на устойчивость системы (1) по первому приближению. Говорят, что система (2) стационарна в первом приближении.
Справедливы следующие утверждения:
1. Если все корни характеристического уравнения
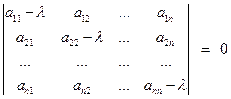 , (4)
, (4)
имеют отрицательные вещественные части, то нулевые решения 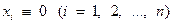 системы (3) и системы (2) асимптотически устойчивы.
системы (3) и системы (2) асимптотически устойчивы.
2. Если хотя бы один корень характеристического уравнения (4) имеет положительную вещественную часть, то нулевое решение системы (2) неустойчиво.
3. Если вещественные части всех корней характеристического уравнения (4) неположительны, причем вещественная часть хотя бы одного корня равна нулю, то исследование на устойчивость по первому приближению, вообще говоря, невозможно (начинают влиять нелинейные члены 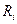 ).
).
Теорема 24. Если система уравнений (2) стационарна в первом приближении, все функции 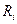 удовлетворяют условиям первого утверждения и хотя бы один из корней характеристического уравнения (4) имеет положительную действительную часть, то точки покоя
удовлетворяют условиям первого утверждения и хотя бы один из корней характеристического уравнения (4) имеет положительную действительную часть, то точки покоя 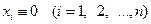 системы (2) и системы (3) неустойчивы, т. е. и в этом случае возможно исследование на устойчивость по первому приближению.
системы (2) и системы (3) неустойчивы, т. е. и в этом случае возможно исследование на устойчивость по первому приближению.
4.3. Критерий Рауса – Гурвица
Пусть имеем линейное дифференциальное уравнение с постоянными вещественными коэффициентами
 (1)
(1)
где  .
.
Нулевое решение 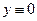 уравнения (1) асимптотически устойчиво, если все корни характеристического уравнения
уравнения (1) асимптотически устойчиво, если все корни характеристического уравнения
 (2)
(2)
имеют отрицательные вещественные части.
Критерий Рауса – Гурвица. Для того, чтобы все корни уравнения (2) имели отрицательные вещественные части, необходимо и достаточно, чтобы были положительными все главные диагональные миноры матрицы Гурвица
 (3)
(3)
Матрица Гурвица составляется так. По главной диагонали выписываются коэффициенты многочлена (2), начиная с 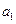 и кончая
и кончая  . Столбцы состоят поочередно из коэффициентов только с нечетными или только с четными индексами, причем в число последних включается
. Столбцы состоят поочередно из коэффициентов только с нечетными или только с четными индексами, причем в число последних включается  коэффициент
коэффициент 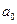 . Все остальные элементы матрицы, отвечающие коэффициентам с индексами, большими n или меньшими 0, полагаются равными нулю. Главные диагональные миноры матрицы Гурвица имеют вид:
. Все остальные элементы матрицы, отвечающие коэффициентам с индексами, большими n или меньшими 0, полагаются равными нулю. Главные диагональные миноры матрицы Гурвица имеют вид:
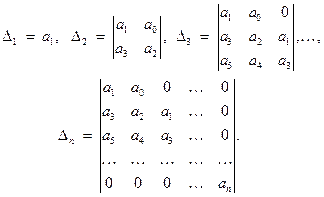
Таким образом, условие Гурвица гласит: для устойчивости решения 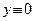 уравнение (1) необходимо и достаточно, чтобы выполнялись соотношения
уравнение (1) необходимо и достаточно, чтобы выполнялись соотношения
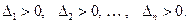 (4)
(4)
Так как 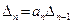 , условие
, условие 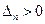 может быть заменено требованием
может быть заменено требованием  .
.
Вычисления можно, например, организовать так. Составляем сначала старший минор матрицы Гурвица  . По нему легко выписываются все младшие миноры
. По нему легко выписываются все младшие миноры 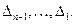 Затем начинаем вычислять
Затем начинаем вычислять 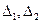 и т.д. последовательно. Если встретился отрицательный минор, решение не устойчиво и дальнейший расчет не нужен.
и т.д. последовательно. Если встретился отрицательный минор, решение не устойчиво и дальнейший расчет не нужен.
Если коэффициенты уравнения (2) заданы как числа, то условия (4) легко проверяются. Если же коэффициенты уравнения (2) содержат буквенные параметры, то вычисление определителей  при больших
при больших 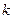 затруднительно.
затруднительно.
Можно показать, что если условия (4) выполнены, то все коэффициенты многочлена (2) положительны:
 . (6)
. (6)
Как уже отмечалось, условия (6) являются необходимыми, но не достаточными для того, чтобы все корни  располагались в левой полуплоскости
располагались в левой полуплоскости 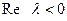 . Однако, при выполнении условий (6) неравенства (4) уже не являются зависимыми. Так, например, при
. Однако, при выполнении условий (6) неравенства (4) уже не являются зависимыми. Так, например, при  условия Рауса – Гурвица приводятся к двум неравенствам:
условия Рауса – Гурвица приводятся к двум неравенствам: 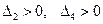 . Это позволило Льенару и Шипару установить другие условия устойчивости, в которых число детерминантных неравенств примерно вдвое меньше, чем в условиях (4).
. Это позволило Льенару и Шипару установить другие условия устойчивости, в которых число детерминантных неравенств примерно вдвое меньше, чем в условиях (4).
Условия Льенара – Шипара. Для того, чтобы многочлен

имел все корни с отрицательными действительными частями, необходимо и достаточно, чтобы:
1) все коэффициенты многочлена  были положительны:
были положительны:
 ,
,
2) имели место детерминантные неравенства
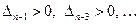
(здесь, как и раньше,  - определитель Гурвица
- определитель Гурвица 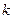 -порядка).
-порядка).
4.4. Геометрический критерий устойчивости (критерий Михайлова)
Пусть имеем линейное дифференциальное уравнение n-го порядка с постоянными вещественными коэффициентами
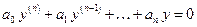 . (1)
. (1)
Его характеристическое уравнение
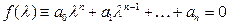 . (2)
. (2)
Критерий Михайлова позволяет вопрос об устойчивости решения д.у. (1) свести к вопросу о расположении корней характеристического уравнения (2) на комплексной плоскости. Последний решается следующим образом.
Полагая 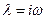 , получим:
, получим:
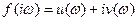 , (3)
, (3)
где
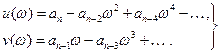 (4)
(4)
Величину 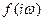 при заданном значении параметра
при заданном значении параметра 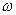 можно изобразить в виде вектора на комплексной плоскости
можно изобразить в виде вектора на комплексной плоскости 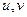 с началом в начале координат (рис. 5). При изменении
с началом в начале координат (рис. 5). При изменении  в интервале
в интервале  конец этого вектора опишет некоторую кривую, каждая точка которой соответствует определенному значению
конец этого вектора опишет некоторую кривую, каждая точка которой соответствует определенному значению 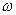 , – так называемую кривую Михайлова для многочлена
, – так называемую кривую Михайлова для многочлена  .
.
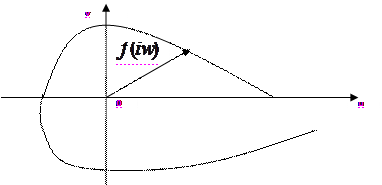
Рис. 5.
Оказывается, что по очертанию кривой Михайлова можно судить о знаках вещественных частей корней многочлена  . Обозначив корни многочлена
. Обозначив корни многочлена  через
через 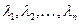 , запишем его в виде
, запишем его в виде
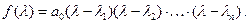
Выражение для кривой Михайлова в этом случае будет
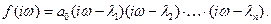 (5)
(5)
Рассмотрим комплексную плоскость  . Легко видеть, что если корень
. Легко видеть, что если корень 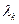 лежит в левой полуплоскости (т.е. имеет отрицательную вещественную часть), то при изменении
лежит в левой полуплоскости (т.е. имеет отрицательную вещественную часть), то при изменении 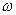 от
от 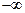 до
до 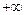 вектор
вектор 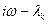 повернется на угол
повернется на угол 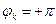 (т.е. сделает пол-оборота против часовой стрелки, см. рис. 6).
(т.е. сделает пол-оборота против часовой стрелки, см. рис. 6).
Аналогично, если корень  лежит в правой полуплоскости, то вектор
лежит в правой полуплоскости, то вектор 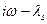 повернется на угол
повернется на угол 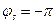 (см. рис.7).
(см. рис.7).
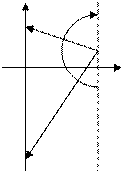
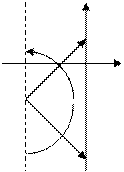
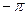

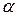
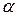
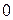

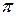
Рис. 6 Рис. 7
Подсчитаем теперь, на какой угол 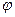 повернется вектор
повернется вектор 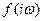 , если
, если 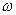 изменяется от
изменяется от 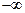 до
до 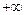 . Известно, что при перемножении комплексных чисел их аргументы складываются. Поэтому
. Известно, что при перемножении комплексных чисел их аргументы складываются. Поэтому 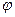 , согласно (5), выразится так:
, согласно (5), выразится так:
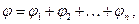
где  - угол поворота вектора
- угол поворота вектора 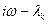 .
.
Если многочлен  степени
степени  имеет
имеет 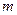 корней с положительными вещественными частями и
корней с положительными вещественными частями и 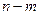 корней с отрицательными, то
корней с отрицательными, то
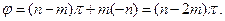 (6)
(6)
Так как функция 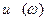 четная, то кривая Михайлова симметрична относительно оси
четная, то кривая Михайлова симметрична относительно оси 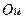 и поэтому достаточно строить часть кривой, отвечающую изменению параметра
и поэтому достаточно строить часть кривой, отвечающую изменению параметра 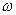 от 0 до
от 0 до 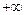 . Тогда формула (6) примет вид:
. Тогда формула (6) примет вид:
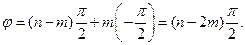 (7)
(7)
Ясно, что для устойчивости решения уравнения (1) необходимо и достаточно, чтобы все корни характеристического уравнения (2) имели отрицательные вещественные части, т.е. в формуле (7) должно быть 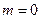 .
.
Отсюда вытекает следующая формулировка критерия Михайлова. Для устойчивости тривиального решения уравнения (1) необходимо и достаточно, чтобы:
1) вектор 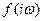 при изменении
при изменении 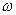 от 0 до
от 0 до 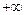 совершил поворот на угол
совершил поворот на угол 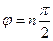 , т.е. сделал
, т.е. сделал 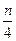 оборотов против часовой стрелки,
оборотов против часовой стрелки,
2) годограф 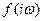 при изменении
при изменении 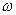 от 0 до
от 0 до 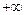 не проходил через нулевую точку.
не проходил через нулевую точку.
Поочередное прохождение квадрантов означает, что кривая поочередно пересекает оси координат. Следовательно, координаты 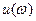 и
и 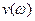 точек кривой Михайлова для устойчивости решения должны поочередно обращаться в нуль. Отсюда вытекает вторая формулировка критерия устойчивости Михайлова. Для устойчивости решения уравнения (1) необходимо (а при условии, что кривая приходится против часовой стрелки – и достаточно), чтобы все корни уравнений
точек кривой Михайлова для устойчивости решения должны поочередно обращаться в нуль. Отсюда вытекает вторая формулировка критерия устойчивости Михайлова. Для устойчивости решения уравнения (1) необходимо (а при условии, что кривая приходится против часовой стрелки – и достаточно), чтобы все корни уравнений  были вещественными и перемежающимися друг с другом, т.е. чтобы между любыми двумя корнями одного из этих уравнений находился корень другого уравнения.
были вещественными и перемежающимися друг с другом, т.е. чтобы между любыми двумя корнями одного из этих уравнений находился корень другого уравнения.
4.5. Метод функций Ляпунова
Пусть имеем вещественную функцию 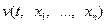 вещественных переменных
вещественных переменных 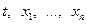 , однозначную, непрерывную в области
, однозначную, непрерывную в области 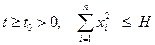 и
и
обращающуюся в нуль, когда 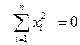 .
.
Функцию 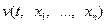 назовем знакопостоянной, если она принимает, кроме нулевых, значения только одного знака при
назовем знакопостоянной, если она принимает, кроме нулевых, значения только одного знака при  достаточно большом и
достаточно большом и 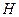 достаточно малом. Такие функции будем называть постоянно-положительными или постоянно-отрицательными. Например, функция
достаточно малом. Такие функции будем называть постоянно-положительными или постоянно-отрицательными. Например, функция 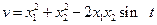 является постоянно положительной (кроме нулевых, она принимает только положительные значения).
является постоянно положительной (кроме нулевых, она принимает только положительные значения).
Если знакопостоянная функция  не зависит от
не зависит от 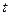 , а величина
, а величина 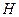 может быть выбрана столь малой, что
может быть выбрана столь малой, что 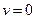 только при
только при 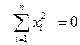 , то функция
, то функция 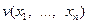 называется знакоопределенной (определенно-положительная или определенно-отрицательная). Например,
называется знакоопределенной (определенно-положительная или определенно-отрицательная). Например,  - определенно-положительная функция.
- определенно-положительная функция.
Знакоопределенная функция  , зависящая явно от
, зависящая явно от 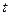 , называется знакоопределенной, если найдется такая не зависящая явно от
, называется знакоопределенной, если найдется такая не зависящая явно от 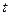 знакоопределенная функция
знакоопределенная функция 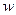 , что одно из двух выражений
, что одно из двух выражений 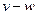 или
или  представляет постоянно-положительную функцию. Так, например, функция
представляет постоянно-положительную функцию. Так, например, функция 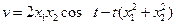 - определенно-отрицательная (для нее
- определенно-отрицательная (для нее 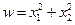 ).
).
Пусть имеем систему дифференциальных уравнений
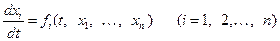 (1)
(1)
Вопрос об устойчивости тривиального решения системы (1) может быть решен с помощью следующих теорем.
Теорема 25 (Теорема А. М. Ляпунова об устойчивости). Если дифференциальные уравнения (1) таковы, что возможно найти знакоопределенную функцию  , производная которой
, производная которой  в силу этих уравнений была бы или знакопостоянной функцией противоположного знака с
в силу этих уравнений была бы или знакопостоянной функцией противоположного знака с  или тождественно равной нулю, то тривиальное решение устойчиво.
или тождественно равной нулю, то тривиальное решение устойчиво.
Производная  , взятая в силу системы (1), имеет вид
, взятая в силу системы (1), имеет вид
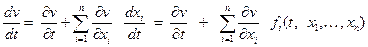 .
.
Если ограниченная функция  такова, что для всякого
такова, что для всякого  , как бы оно мало ни было, найдется такое число
, как бы оно мало ни было, найдется такое число 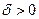 , что при
, что при 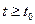 и
и 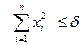 будет выполняться неравенство
будет выполняться неравенство 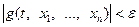 , то говорят что
, то говорят что 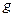 допускает бесконечно малый высший предел.
допускает бесконечно малый высший предел.
Замечание. Всякая не зависящая явно от 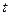 непрерывная функция
непрерывная функция 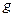 допускает бесконечно малый высший предел.
допускает бесконечно малый высший предел.
Теорема 26 (Дополнение А. М. Ляпунова об асимптотической устойчивости.) Если знакоопределенная функция  допускает бесконечно малый высший предел, а ее производная
допускает бесконечно малый высший предел, а ее производная  , составленная в силу системы (1), является знакоопределенной функцией противоположного знака, то тривиальное решение асимптотически устойчиво.
, составленная в силу системы (1), является знакоопределенной функцией противоположного знака, то тривиальное решение асимптотически устойчиво.
Назовем областью 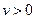 какую-нибудь область окрестности
какую-нибудь область окрестности  начала координат пространства переменных
начала координат пространства переменных 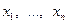 , ограниченную поверхность
, ограниченную поверхность 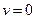 , в которой функция
, в которой функция  принимает положительные значения.
принимает положительные значения.
Допустим, что функция  обладает следующими свойствами:
обладает следующими свойствами:
1) при сколь угодно больших значениях 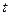 в сколь угодно малой окрестности начало координат существует область
в сколь угодно малой окрестности начало координат существует область 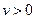 ;
;
2) в области 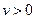 функция
функция  ограничена;
ограничена;
3) в области 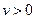 производная
производная  , составленная в силу системы (1), определенно-положительная.
, составленная в силу системы (1), определенно-положительная.
Теорема 27 (Теорема Н. Г. Четаева о неустойчивости). Если для системы дифференциальных уравнений (1) можно найти функцию, удовлетворяющую условиям 1), 2), 3), то тривиальное решение этой системы неустойчиво.
Функции 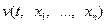 , фигурирующие в приведенных выше теоремах, называются функциями Ляпунова.
, фигурирующие в приведенных выше теоремах, называются функциями Ляпунова.
Замечание. Если в системе (1) все 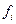 не зависят явно от
не зависят явно от 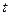 , то функцию Ляпунова нужно искать как не зависящую явно от
, то функцию Ляпунова нужно искать как не зависящую явно от 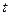 .
.
Дата публикования: 2015-09-17; Прочитано: 1034 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
