 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уравнение Клеро
|
|
В случае 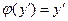 уравнение Лагранжа принимает вид
уравнение Лагранжа принимает вид

и называется уравнением Клеро.
Общее решение уравнения Клеро получается простой заменой в уравнении производной 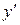 произвольной постоянной
произвольной постоянной 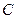 :
: 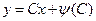 - т.е. это семейство прямых. Кроме того, существует решение, не вытекающее из общего, которое в параметрической форме записывается так:
- т.е. это семейство прямых. Кроме того, существует решение, не вытекающее из общего, которое в параметрической форме записывается так:
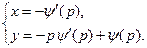
Это решение - особое решение и является огибающей семейства прямых 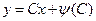 .
.
Таким образом, интегральные кривые уравнения Клеро состоят из некоторой кривой и всех ее касательных.
1.9. Задачи на составление дифференциальных
уравнений
Решение любой задачи прикладного значения обычно состоит из трех частей:
1) составление дифференциального уравнения;
2) решение этого уравнения;
3) исследование решения.
1.9.1. Геометрические задачи
При решении геометрических задач полезно придерживаться следующей последовательности действий:
1) сделать чертеж и ввести обозначения. Например, 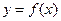 - уравнение искомой линии и т.п.;
- уравнение искомой линии и т.п.;
2) отделить условия, имеющие место в произвольной точке искомого геометрического места, от условий, имеющих место лишь в отдельных фиксированных точках. Другими словами, выделить начальные условия (их вначале, при составлении дифференциального уравнения, не учитывать);
3) выразить все упомянутые в задаче величины через 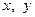 и
и 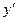 , учитывая при этом геометрический смысл производной;
, учитывая при этом геометрический смысл производной;
4) на основании условия задачи составить дифференциальное уравнение семейства искомых уравнений;
5) найти общее решение полученного дифференциального уравнения, а затем по начальным условиям найти конкретную интегральную кривую.
1.9.2. Физические задачи
При решении задач с физическим содержанием, так же как в случае геометрических задач, можно предложить следующую последовательность действий:
1) установить, какому закону подчиняется рассматриваемый процесс,
2) решить, что выбрать за независимое переменное, например, время 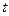 , и что за искомую функцию, например,
, и что за искомую функцию, например, 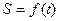 ,
,
3) исходя из условий задачи, определить начальные условия. Например, 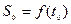 ,
,
4) выразить все фигурирующие в задаче величины через 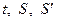 , используя при этом физический смысл производной как скорость изменения переменной
, используя при этом физический смысл производной как скорость изменения переменной 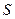 в изучаемом процессе,
в изучаемом процессе,
5) исходя из условий задачи и на основании физического закона, которому подчиняется данный процесс, составить дифференциальное уравнение,
6) найти общий интеграл дифференциального уравнения,
7) по начальным условиям найти частное решение.
ГЛАВА 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
2.1. Дифференциальные уравнения высших порядков, допускающие понижение порядка
I. Уравнения вида 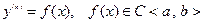
Для нахождения общего решения уравнения достаточно проинтегрировать последовательно n раз данное уравнение:
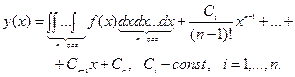
II. Уравнения вида 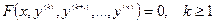
Д.у. такого вида не содержат 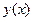 . Порядок понижается на
. Порядок понижается на  подстановкой
подстановкой 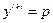 , где
, где 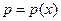 - новая искомая функция,
- новая искомая функция, 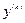 - младшая производная, входящая в уравнение.
- младшая производная, входящая в уравнение.
III. Уравнения вида 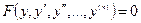
Уравнения этого типа не содержат аргумента 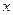 . Порядок понижается на единицу при помощи подстановки
. Порядок понижается на единицу при помощи подстановки 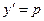 , но, в отличие от п.II, здесь
, но, в отличие от п.II, здесь 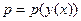 , т.е. композиция двух функций
, т.е. композиция двух функций 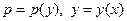 , поэтому
, поэтому
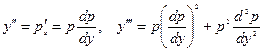 .
.
IV. Уравнения вида 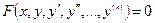 , где
, где 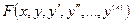 - однородная относительно переменных
- однородная относительно переменных 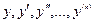 функция
функция
Порядок уравнений такого типа понижается на единицу в результате подстановки 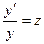 , при этом
, при этом 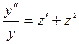 .
.
Замечание 14. Порядок такого уравнения может быть понижен на единицу и подстановкой  .
.
2.2. Линейные дифференциальные уравнения n-го порядка
Линейным однородным дифференциальным уравнением (ЛОДУ) n-го порядка называется д.у. вида
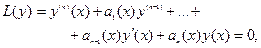 (1)
(1)
где 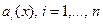 - заданные непрерывные на промежутке
- заданные непрерывные на промежутке 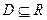 функции.
функции.
Если для системы функций 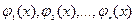 , заданных на D, не существует ненулевого набора постоянных
, заданных на D, не существует ненулевого набора постоянных  , чтобы имело место равенство
, чтобы имело место равенство 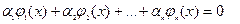 при всех
при всех 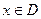 , то данная система функций называется линейно независимой на множестве D.
, то данная система функций называется линейно независимой на множестве D.
Пусть на D задана система (n-1) раз дифференцируемых функций 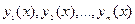 . Тогда определитель
. Тогда определитель
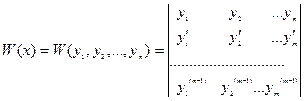
называется определителем Вронского данной системы функций.
Теорема 10 (Необходимое и достаточное условие линейной независимости решений ЛОДУ). Для того, чтобы решения 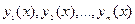 ЛОДУ (1) были линейно независимы на D, необходимо и достаточно, чтобы
ЛОДУ (1) были линейно независимы на D, необходимо и достаточно, чтобы 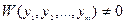 на D.
на D.
Любая система из n линейно независимых частных решений 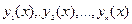 ЛОДУ (1) называется фундаментальной системой решений этого уравнения.
ЛОДУ (1) называется фундаментальной системой решений этого уравнения.
Теорема 11 (О существовании фундаментальной системы частных решений ЛОДУ). У всякого ЛОДУ (1) существует ее фундаментальная система из n частных решений, и таких фундаментальных систем решений у ЛОДУ (2) существует бесчисленное множество.
Теорема 12 (О структуре общего решения ЛОДУ). Если 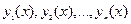 образуют фундаментальную систему частных решений ЛОДУ (2), то их линейная комбинация
образуют фундаментальную систему частных решений ЛОДУ (2), то их линейная комбинация
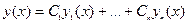 , (2)
, (2)
где 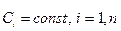 , является общим решением ЛОДУ (1) в том смысле, что каждое частное решение ЛОДУ (1) может быть получено из (2) при надлежащем выборе постоянных
, является общим решением ЛОДУ (1) в том смысле, что каждое частное решение ЛОДУ (1) может быть получено из (2) при надлежащем выборе постоянных 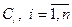 .
.
2.2.1. Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами
Линейным однородным дифференциальным уравнением (ЛОДУ) n-го порядка с постоянными коэффициентами называется д.у. вида
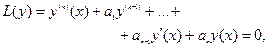 (3)
(3)
где 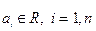 .
.
Дата публикования: 2015-09-17; Прочитано: 721 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
