Применение рядов к решению дифференциальных уравнений

Пусть требуется проинтегрировать дифференциальное уравнение второго порядка

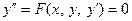. (1)

Если его решение не выражается через элементарные функции в конечном виде или обычные способы решения слишком трудоемки, то в отдельных случаях его решение (частное или общее) удается отыскать в виде некоторого степенного ряда.

I. Способ последовательных дифференцирований применяется, когда требуется найти частное решение 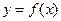уравнения (1), удовлетворяющее начальным условиям 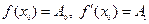. Если в окрестности точки 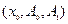уравнение (1) удовлетворяет условиям теоремы существования и единственности решения задачи Коши для д.у. второго порядка, то можно попытаться искать его частное решение в виде ряда Тейлора

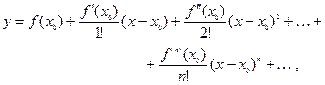(2)

первые два члена которого известны, так как 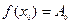, 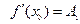. (Заметим, что сама теорема существования и единственности решения задачи Коши не обеспечивает существования решения уравнения (1) в виде степенного ряда (1).)

Из уравнения (1) находим 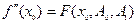. Если затем продифференцировать уравнение (1) по 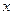, то можно найти сколько угодно производных искомой функции 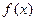в точке :

.

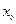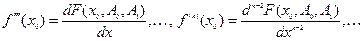Здесь под символами 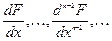понимаются полные производные по 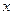от функции 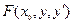в предположении, что и 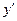зависят от 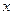, т.е.

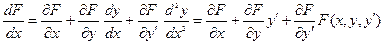
и т.д. Подставляя найденные производные функции 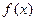в разложение (2), получаем искомое решение

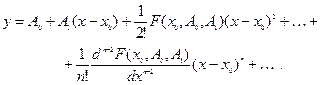
Рассмотренный способ, разумеется, применим для решения дифференциальных уравнений любого порядка.

II. Способ неопределенных коэффициентов применяется, когда требуется найти либо частное решение 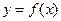уравнения (1), удовлетворяющее начальным условиям 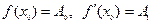, либо общее решение в виде степенного ряда по степеням .

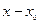Если уравнение (1) в окрестности точки 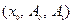удовлетворяет условиям теоремы существования и единственности решения задачи Коши для дифференциального уравнения второго порядка, то его частное (или общее) решение можно искать в виде ряда

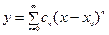, (3)

коэффициенты 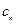которого подлежат определению.

Если точка 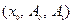является особой для уравнения (1), то его частное (или общее) решение следует искать в виде обобщенного степенного ряда

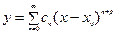, (4)

где 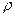не обязательно целое число и подлежит определению вместе с коэффициентами ряда.

Чтобы определить коэффициенты 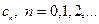, искомого ряда (3) или (4), поступают следующим образом:

1) дважды дифференцируют ряд (3) (или (4) с неизвестными коэффициентами и находят таким образом и ;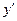

2) подставляют разложения 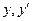и 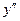в степенные ряды в исходное дифференциальное уравнение (1);

3) представляют функцию 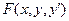в виде степенного ряда по степеням 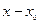, после чего равенство (1) принимает вид равенства двух степенных рядов;

4) путем приравнивания коэффициентов полученных рядов при одинаковых степенях разностей 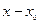получают уравнения для определения неизвестных коэффициентов 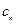; если решение ищется в виде (4), то, приравнивая коэффициенты при наименьшей степени разности 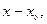получают так называемое определяющее уравнение, из которого находят всевозможные значения параметра ;

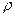5) из полученных уравнений находят коэффициенты 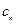и подставляют их в искомый ряд (3); если решение ищется в виде (4), то коэффициенты 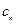находят для каждого значения 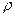и таким образом получают столько частных решений, сколько значений имеет параметр .

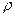Полученное в виде ряда решение может быть исследовано на сходимость известными признаками. Если полученный ряд сходится в некоторой области, то обязательно к решению дифференциального уравнения, так как его коэффициенты определялись из условия, чтобы сумма ряда являлась решением.

Описанный способ решения дифференциальных уравнений, разумеется, распространяется на уравнения любого порядка. Чаще всего этот способ применяют для решения линейных дифференциальных уравнений, для которых справедливы следующие теоремы.

1. Если функциональные коэффициенты 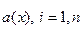, линейного дифференциального уравнения

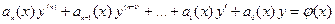
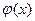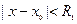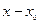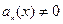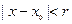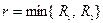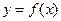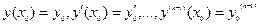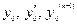и его правая часть суть функции, разложимые в интервале в степенные ряды по степеням , а в интервале , то в интервале , где , существует единственное решение данного уравнения, удовлетворяющее начальным условиям , где - произвольные числа, в виде сходящегося степенного ряда (3).

Из этой теоремы, в частности, вытекает, что есл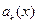и и 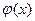суть многочлены, а 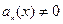для всех 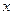, то упомянутое выше решение будет рядом вида (3), сходящимся на всей числовой оси.

2. Если линейное дифференциальное уравнение второго порядка представимо в виде

,

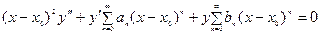где 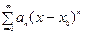и 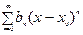- сходящиеся в интервале 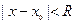степенные ряды, в которых коэффициенты 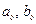и 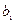не равны нулю одновременно, то существует, по крайней мере, одно частное решение 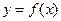данного уравнения в виде степенного ряда (4), сходящегося в интервале .

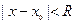ГЛАВА III. CИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Система обыкновенных дифференциальных уравнений первого порядка вида

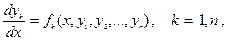(1)

где 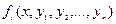- заданные достаточно гладкие функции, 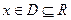- независимая переменная, 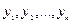- неизвестные функции от 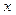, называется нормальной системой.

Решением системы (1) в интервале (a,b) называется совокупность любых 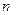функций

,

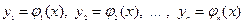определенных и непрерывно дифференцируемых в интервале (a,b), если они обращают уравнения системы (1) в тождества, справедливые для всех значений 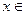(a,b).

Задачей Коши для системы (1) называется задача нахождения решения 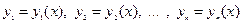этой системы, удовлетворяющего начальным условиям

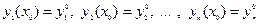, (2)

где 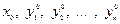- заданные числа.

Теорема Пикара (Теорема существования и единственности решения задачи Коши). Пусть имеем нормальную систему дифференциальных уравнений (1) и пусть функции 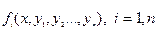определены в некоторой n+1 мерной области D изменения переменных 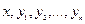. Если существует окрестность W точки 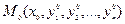, в которой функции 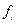а) непрерывны, б) имеют ограниченные частные производные по переменным 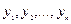, то найдется интервал 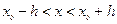изменения 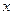, в котором существует единственное решение нормальной системы (1), удовлетворяющее начальным условиям (2).

Система 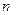дифференцируемых функций

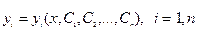, (3)

независимой переменной 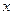и n произвольных постоянных 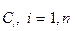, называется общим решением нормальной системы (1), если: 1) при любых допустимых значениях 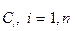, система функций (3) обращает уравнения (1) в тождества, 2) в области, где выполняются условия теоремы Пикара, функции (3) решают любую задачу Коши.

Линейная неоднородная система дифференциальных уравнений имеет вид

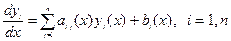, (4)

где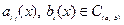

Систему (4) можно коротко записать в виде одного векторно-матричного уравнения

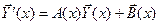, (5)

где

.

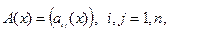
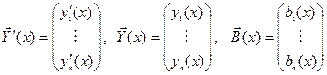Соответствующая линейная однородная система имеет вид

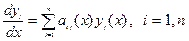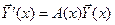или . (6)

Система из n линейно независимых частных решений однородной системы (6) называется ее фундаментальной системой решений.

Теорема 21 (О структуре общего решения линейной однородной системы). Если 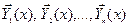образуют на 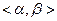фундаментальную систему частных решений однородной системы (6), то их линейная комбинация

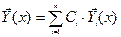(7)

является общим решением системы (6) в том смысле, что каждое частное решение системы (6) может быть получено из (7) при надлежащем выборе .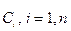

Теорема 22 (О структуре общего решения линейной неоднородной системы). Общее решение линейной неоднородной системы (4) или (5) есть сумма какого-либо его частного решения и общего решения соответствующей линейной однородной системы (6).

3.1. Метод исключения (сведение системы дифференциальных уравнений к одному уравнению)

Рассмотрим нормальную систему дифференциальных уравнений

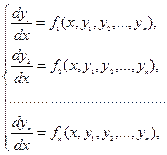(1)

где 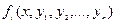- заданные достаточно гладкие функции, .

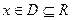Проинтегрируем систему, т. е. определим функции 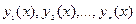, удовлетворяющие на промежутке D системе (1) и данным начальным условиям:

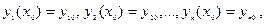(2)

где 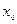- внутренняя точка D, 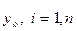- заданные действительные числа.

Для этого вначале дифференцируем по 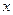первое из уравнений (1):

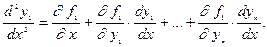
Заменяя производные 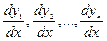их выражениями 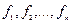из уравнений (1), будем иметь уравнение

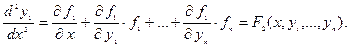
Дифференцируя по 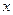полученное уравнение и поступая аналогично предыдущему, найдем:

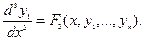
Продолжая далее таким же образом, получим, наконец, уравнение

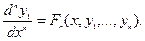
Итак, мы приходим к следующей системе:

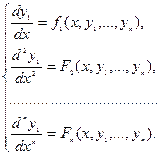(3)

Из первых n-1 уравнений определим 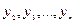, выразив их через 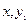, и производные :

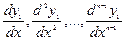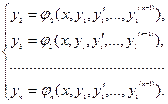(4)

Подставляя эти выражения в последнее из уравнений системы (3), получим уравнение n-го порядка для определения :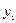

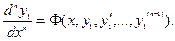(5)

Решая это уравнение, определим :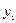

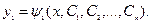(6)

Дифференцируя последнее выражение n-1 раз, найдем производные 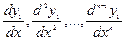как функции от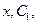 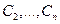. Подставляя эти функции в уравнения системы (4), определяем :

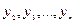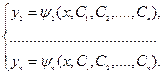(7)

Для того, чтобы полученное решение удовлетворяло заданным начальным условиям (2), остается лишь найти из уравнений (6) и (7) соответствующие значения постоянных 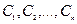(подобно тому, как это делается в случае одного дифференциального уравнения).

Замечание 17. Если система (1) линейна относительно искомых функций, то и уравнение (5) будет линейным.

Замечание 18. В приведенных рассуждениях предполагалось, что из первых n-1 уравнений системы (3) можно определить функции 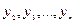. Может случиться, что переменные 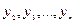исключаются не из n, а из меньшего числа уравнений. Тогда для определения получается уравнение, порядок которого ниже n.

3.2. Линейная однородная система дифференциальных уравнений с постоянными коэффициентами. Метод Эйлера

Пусть мы имеем линейную однородную систему дифференциальных уравнений с постоянными коэффициентами

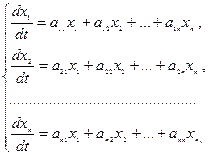(1)

где коэффициенты 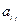суть постоянные, 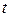- аргумент, 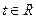, 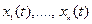- искомые функции.

Будем искать частное решение системы в следующем виде:

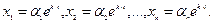(2)

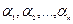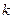Требуется определить постоянные и так, чтобы функции 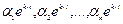удовлетворяли системе уравнений (1). Подставляя их в систему (1), получим:

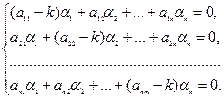(3)

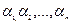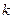Выберем и так, чтобы удовлетворялась система (3). Эта система есть система линейных алгебраических уравнений относительно 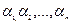. Составим определитель системы (3):

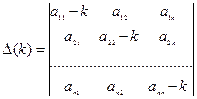. (4)

Если 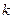таково, что определитель D отличается от нуля, то система (3) имеет только нулевые решения 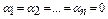, а, следовательно, формулы (2) дают только тривиальные решения:

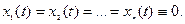
Таким образом, нетривиальные решения (2) мы получим только при таких 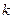, при которых определитель (4) обращается в нуль. Мы приходим к уравнению n- го порядка для определения :

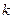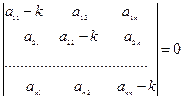(5)

Это уравнение называется характеристическим уравнением для системы (1), его корни называются корнями характеристического уравнени я.

Рассмотрим возможные случаи.

1. Корни характеристического уравнения действительные и различные.

Обозначим через 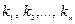корни характеристического уравнения. Для каждого корня 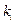напишем систему (3) и определим коэффициенты 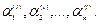Можно показать, что один из них произвольный, его можно считать равным единице. Таким образом, получаем:

для корня 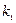решение системы (1)

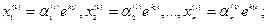
для корня 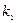решение системы (1)

........................

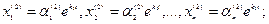
для корня 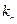решение системы (1)

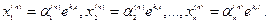
Путем непосредственной подстановки в уравнения можно убедиться, что система функций

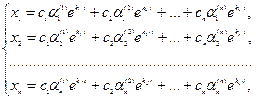(6)

где 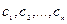- произвольные постоянные, тоже является решением системы дифференциальных уравнений (1). Это есть общее решение системы (1). Легко показать, что можно найти такие значения постоянных, при которых решение будет удовлетворять заданным начальным условиям.

2. Корни характеристического уравнения различные, но среди них есть комплексные.

Пусть среди корней характеристического уравнения имеются два комплексных сопряженных корня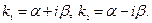

Этим корням будут соответствовать решения

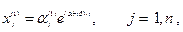(7)

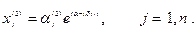(8)

Коэффициенты определяются из системы уравнений (3). Действительные и мнимые части комплексного решения тоже являются решениями.

Т.о., мы получаем два частных решения:

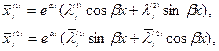(9)

где 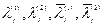- действительные числа, определяемые через 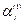и .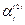

Соответствующие комбинации функций (9) войдут в общее решение системы.

3. Среди корней характеристического уравнения имеются действительные кратные.

Если для кратного корня 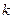имеется столько линейно независимых собственных векторов a1, a2,..., an, какова его кратность, то ему соответствует решение

.

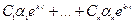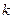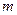Если для корня кратности имеется только линейно независимых собственных векторов и 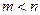, то решение, соответствующее этому 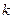, можно искать в виде произведения многочлена степени 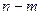на 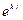, т.е. в виде

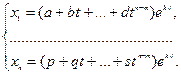(12)

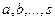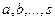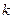Чтобы найти коэффициенты подобных членов в левой и правой частях уравнений, получим систему линейных алгебраических уравнений относительно . Надо найти общее решение этой системы. Коэффициенты должны зависеть от произвольных постоянных, где - кратность корня . Найдя для каждого 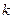решения указанного вида и сложив их, получим общее решение системы (1).