 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Условия существования определенного интеграла
|
|
Теорема 5 (необходимое условие интегрируемости функции). Если 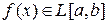 , то она ограничена на
, то она ограничена на 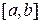 .
.
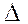 Предположим противное, т.е. допустим, что
Предположим противное, т.е. допустим, что  неограничена на
неограничена на 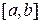 . Покажем, что в этом случае интегральную сумму
. Покажем, что в этом случае интегральную сумму  можно за счет выбора точек
можно за счет выбора точек 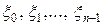 сделать сколь угодно большой при любом разбиении отрезка
сделать сколь угодно большой при любом разбиении отрезка 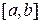 .
.
Действительно, так как  неограничена на
неограничена на 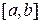 , то при любом разбиении отрезка
, то при любом разбиении отрезка 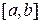 , по крайней мере, на одном из отрезков
, по крайней мере, на одном из отрезков 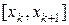 функция
функция  будет неограничена. Пусть для определенности она неограничена на отрезке
будет неограничена. Пусть для определенности она неограничена на отрезке 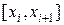 . Интегральную сумму
. Интегральную сумму  представим в виде
представим в виде
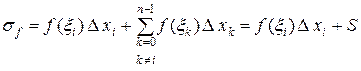 .
.
Числа 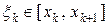 во втором слагаемом выберем произвольным образом.
во втором слагаемом выберем произвольным образом.
Зададим произвольное число 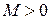 и возьмем такую точку
и возьмем такую точку 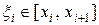 , чтобы
, чтобы
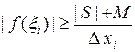 .
.
Выбрать такую точку 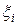 можно всегда в силу неограниченности функции
можно всегда в силу неограниченности функции  на
на 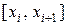 . Тогда
. Тогда 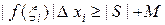 , и значит,
, и значит,
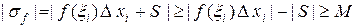 ,
,
т.е. интегральная сумма  по модулю больше любого наперед заданного числа. Поэтому интегральная сумма
по модулю больше любого наперед заданного числа. Поэтому интегральная сумма  не имеет конечного предела при
не имеет конечного предела при 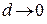 , а это означает, что определенный интеграл от неограниченной функции не существует. ▲
, а это означает, что определенный интеграл от неограниченной функции не существует. ▲
Замечание. Обратная теорема неверна, т.е. условие ограниченности функции является необходимым, но не достаточным условием интегрируемости функции. Докажем это утверждение.
Пример. Рассмотрим функцию Дирихле на отрезке 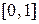 :
:
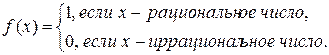
Функция Дирихле, очевидно, ограничена: 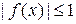 . Однако она неинтегрируема на
. Однако она неинтегрируема на 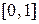 . Покажем это. Если при любом разбиении отрезка
. Покажем это. Если при любом разбиении отрезка 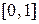 выбрать рациональные
выбрать рациональные 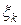 (
(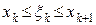 ), то получим
), то получим
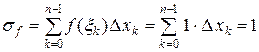 ,
,
а если взять числа 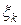 иррациональными, то получим
иррациональными, то получим
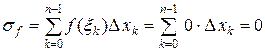 .
.
Таким образом, при разбиении отрезка 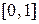 на сколь угодно малые отрезки интегральная сумма
на сколь угодно малые отрезки интегральная сумма  может принимать как значение, равное
может принимать как значение, равное 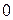 , так и значение, равное
, так и значение, равное 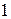 . Поэтому интегральная сумма
. Поэтому интегральная сумма  при
при 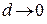 предела не имеет.
предела не имеет.
Теорема 6 (достаточное условие интегрируемости функции). Если функция  ограничена на отрезке
ограничена на отрезке 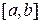 и имеет на нем конечное число точек разрыва, то
и имеет на нем конечное число точек разрыва, то 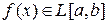 .
.
(Без доказательства)
Следствие. Если 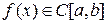 , то
, то 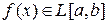 (т.е. имеет место включение
(т.е. имеет место включение 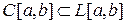 .
.
Дата публикования: 2015-09-17; Прочитано: 2047 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
