 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Иррациональные функции
|
|
а) Интегралы вида 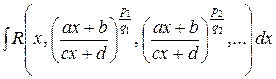 ,
,
где 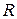 – рациональная функция и
– рациональная функция и 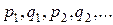 – целые числа.
– целые числа.
Интегралы такого вида вычисляются с помощью подстановки
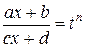 ,
,
где 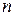 – общий знаменатель дробей
– общий знаменатель дробей 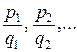 (наименьшее общее кратное чисел
(наименьшее общее кратное чисел 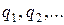 ). В результате этой подстановки подынтегральная функция преобразуется в рациональную.
). В результате этой подстановки подынтегральная функция преобразуется в рациональную.
Пример. Вычислить 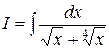 .
.
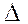 Положим
Положим 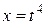 ; тогда
; тогда 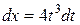 и
и
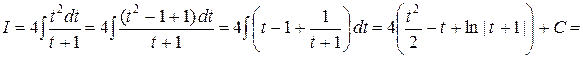
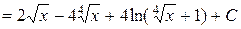 . ▲
. ▲
б) Интегралы вида 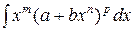 .
.
Подынтегральное выражение 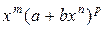 называют дифференциальным биномом.
называют дифференциальным биномом.
Данный интеграл выражается в конечном виде (т.е. первообразная представляет собой элементарную функцию) лишь в следующих трех случаях (этот результат получен выдающимся русским математиком и механиком Пафнутием Львовичем Чебышёвым (1821 – 1894)):
1) если 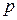 – целое число. В этом случае используют разложение на слагаемые по формуле бинома Ньютона;
– целое число. В этом случае используют разложение на слагаемые по формуле бинома Ньютона;
2) если 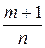 – целое число. Тогда применяется подстановка
– целое число. Тогда применяется подстановка 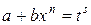 , где
, где 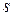 – знаменатель дроби
– знаменатель дроби  ;
;
3) если 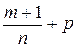 – целое число. В этом случае используется подстановка
– целое число. В этом случае используется подстановка 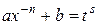 , где, по-прежнему,
, где, по-прежнему, 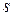 – знаменатель дроби
– знаменатель дроби 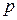 .
.
Пример. Вычислить
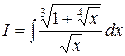 .
.
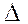 Перепишем исходный интеграл
Перепишем исходный интеграл
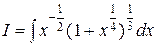 .
.
Это интеграл от дифференциального бинома, где 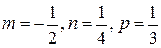 ;
; 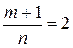 . Следовательно, имеет место случай 2) интегрируемости.
. Следовательно, имеет место случай 2) интегрируемости.
Подстановка 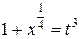 дает:
дает: 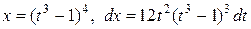 . Поэтому
. Поэтому
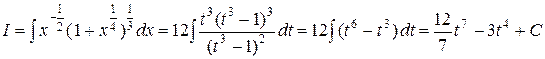 ,
,
где 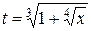 . ▲
. ▲
в) Интегралы вида 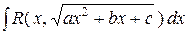 ,
,
где 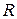 – рациональная функция.
– рациональная функция.
Такие выражения всегда интегрируются в конечном виде. Один из возможных методов интегрирования состоит в следующем.
Выделяем полный квадрат в квадратном трехчлене 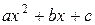 и совершаем замену переменной по формуле
и совершаем замену переменной по формуле 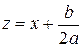 ; после этого исходный интеграл сводится к одному из следующих трех типов:
; после этого исходный интеграл сводится к одному из следующих трех типов:
1) 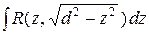 , 2)
, 2) 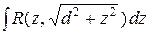 , 3)
, 3) 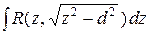 .
.
Эти три типа интегралов вычисляются с помощью тригонометрической (или гиперболической) подстановки соответственно
1) 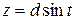 или
или 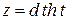 ,
,
2) 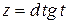 или
или 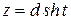 ,
,
3) 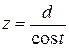 или
или 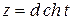 .
.
В результате этих подстановок указанные интегралы приводятся к виду 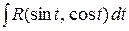 или
или 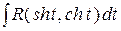 . Интегралы от гиперболических функций вычисляются аналогично интегралам от тригонометрических функций.
. Интегралы от гиперболических функций вычисляются аналогично интегралам от тригонометрических функций.
В частном случае, когда требуется вычислить интегралы вида
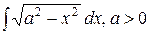 , и
, и 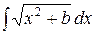 ,
,
можно обойтись без замены переменной. Вычислим первый из них:
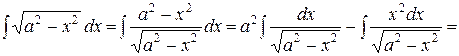
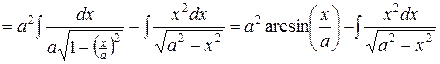 .
.
Для вычисления последнего интеграла воспользуемся методом интегрирования по частям:
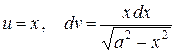 .
.
Тогда
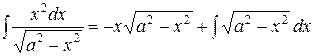 .
.
Вернемся к исходному интегралу:
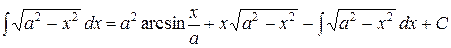 .
.
Из последнего равенства получаем
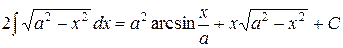
и, разделив обе части на два, найдем
 .
.
Поступая аналогично для 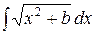 , получим
, получим
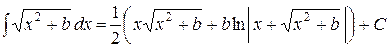 .
.
4. О «неберущихся» интегралах. Рассмотренные методы и приемы интегрирования не исчерпывают всех классов интегрируемых элементарных функций. В то же время из всего изложенного следует, что техника интегрирования сложнее по сравнению с дифференцированием. Не существует общего универсального метода интегрирования, поэтому этот раздел математики мало алгоритмичен. Необходимы определенные навыки и изобретательность, которые приобретаются на практике в результате решения большого числа примеров. Возникает вопрос о возможности вычисления интеграла от любой элементарной функции. Все элементарные функции дифференцируемы и их производные снова являются элементарными функциями. Об интегрировании функций это сказать нельзя. Существует немало элементарных функций, интегралы от которых не выражаются через элементарные функции (говорят: «не интегрируются в конечном виде»), например:
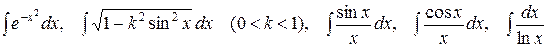 .
.
Подчеркнем, что эти интегралы существуют, но они определяют функции, не являющиеся элементарными.
Было бы ошибочно считать, что «неберущиеся» интегралы являются экзотикой, придуманной математиками. На самом деле, именно «берущиеся» интегралы следует считать экзотикой; они представляют собой редкое исключение в многообразии «неберущихся» интегралов. К «неберущимся» интегралам приводят многие теоретические и практические задачи. Например, первый из приведенных интегралов возникает в задачах теории вероятностей и статистики, второй (относящийся к так называемым эллиптическим интегралам) – в задачах механики.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1. Понятие определенного интеграла. Пусть функция  определена на отрезке
определена на отрезке 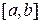 . Назовем разбиением отрезка
. Назовем разбиением отрезка 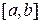 совокупность точек
совокупность точек 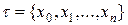 :
: 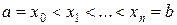 . Точки
. Точки  (
(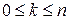 ) будем называть точками разбиения. В каждом из полученных отрезков разбиения
) будем называть точками разбиения. В каждом из полученных отрезков разбиения 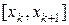 выберем произвольную точку
выберем произвольную точку 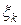 (
(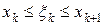 ). Символом
). Символом 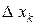 обозначим разность
обозначим разность 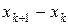 (
(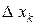 – длина отрезка разбиения).
– длина отрезка разбиения).
Образуем сумму
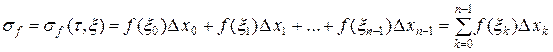 .
.
Эту сумму называют интегральной суммой (для) функции  на
на 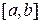 , соответствующей данному разбиению
, соответствующей данному разбиению 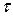 отрезка
отрезка 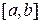 и данному выбору промежуточных точек
и данному выбору промежуточных точек 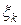 .
.
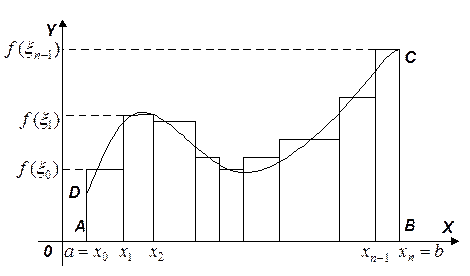 |
Для того чтобы выяснить геометрический смысл интегральной суммы
 , изобразим график функции
, изобразим график функции 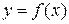 на отрезке
на отрезке 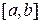 (рис. 1).
(рис. 1).Рис. 1.
Ясно, что  – это сумма площадей прямоугольников с основаниями
– это сумма площадей прямоугольников с основаниями 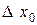 ,
, 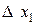 , …,
, …, 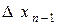 и высотами
и высотами 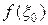 ,
, 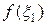 ,…,
,…, 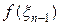 соответственно (рис. 1 сделан для случая, когда
соответственно (рис. 1 сделан для случая, когда 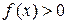 ). Очевидно также, что
). Очевидно также, что  представляет собой приближенное значение площади криволинейной трапеции
представляет собой приближенное значение площади криволинейной трапеции 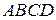 (рис. 1), и это приближенное значение тем точнее, чем «мельче» разбиение отрезка
(рис. 1), и это приближенное значение тем точнее, чем «мельче» разбиение отрезка 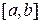 точками
точками 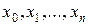 . При этом площадь
. При этом площадь 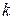 -го прямоугольника на рис. 1 равна
-го прямоугольника на рис. 1 равна 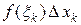 .
.
Обозначим через 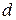 длину наибольшего отрезка разбиения, т.е.
длину наибольшего отрезка разбиения, т.е. 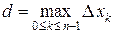 . Число
. Число 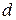 назовем мелкостью разбиения отрезка
назовем мелкостью разбиения отрезка 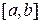 .
.
Определение 1. Число 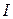 называется пределом интегральных сумм
называется пределом интегральных сумм 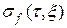 при
при 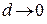 , если
, если 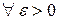
 такое, что для всякого разбиения
такое, что для всякого разбиения 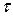 , у которого
, у которого 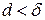 , выполняется неравенство
, выполняется неравенство  при любом выборе промежуточных точек
при любом выборе промежуточных точек 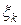 .
.
Определение 2. Функция  называется интегрируемой (по Риману) на отрезке
называется интегрируемой (по Риману) на отрезке 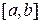 , если существует конечный предел
, если существует конечный предел
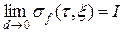 .
.
При этом число 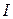 называется определенным интегралом от функции
называется определенным интегралом от функции  по отрезку
по отрезку 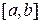 и обозначается символом
и обозначается символом
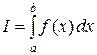 .
.
Числа 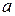 и
и 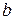 называют нижним и верхним пределами интегрирования,
называют нижним и верхним пределами интегрирования,  – подынтегральной функцией, а
– подынтегральной функцией, а 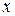 – переменной интегрирования.
– переменной интегрирования.
В отличие от неопределенного интеграла, определенный интеграл представляет собой число, а не функцию. Если интеграл существует, то это число определяется однозначно и зависит только от вида функции  и от чисел
и от чисел 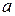 и
и 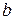 . Отсюда, в частности, следует, что определенный интеграл не зависит от выбора обозначения для переменной интегрирования:
. Отсюда, в частности, следует, что определенный интеграл не зависит от выбора обозначения для переменной интегрирования:
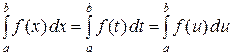 и т.д.
и т.д.
Вычисление определенного интеграла в соответствии с приведенным определением связано с трудностями и громоздкими подсчетами. Поэтому чаще используют другие подходы, о которых будет говориться ниже.
Пусть функция  является интегрируемой на отрезке
является интегрируемой на отрезке 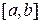 функцией. В этом случае будем писать
функцией. В этом случае будем писать 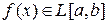 . Здесь
. Здесь  обозначает множество всех интегрируемых на
обозначает множество всех интегрируемых на 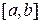 функций (вспомните, что представляют из себя множества
функций (вспомните, что представляют из себя множества 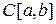 и
и 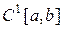 ).
).
Дата публикования: 2015-09-17; Прочитано: 1389 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
