 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Разложение некоторых элементарных функций в ряд Тейлора
|
|
Задача разложения функции в ряд Тейлора в окрестности точки 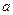 решается в следующем порядке:
решается в следующем порядке:
1. Находятся последовательно 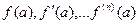 .
.
2. Записываются 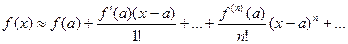 (1).
(1).
3. Находим интервал сходимости ряда (1): 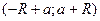 .
.
4. Записываем остаточный член 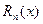 в каком-то виде.
в каком-то виде.
5. Находим те точки 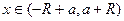 , для которых
, для которых 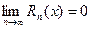 .
.
После выполнения этих пунктов в (1) вместо 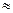 можно поставить равенство
можно поставить равенство 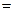 .
.
Функция  .
.
Пусть задана функция  , она бесконечно дифференцируемая и
, она бесконечно дифференцируемая и 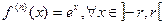 , где
, где 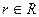 .
.
Найдем коэффициенты разложения 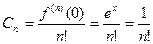 , тогда
, тогда
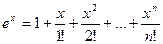 -это ряд Маклорена для функции
-это ряд Маклорена для функции 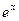 , который сходится к этой функции на всей числовой прямой.
, который сходится к этой функции на всей числовой прямой.
Функция 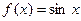 .
.
Найдем ее производные
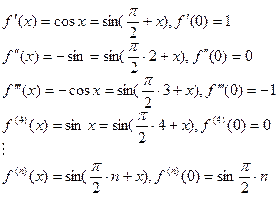
Вычислим коэффициенты в формуле Тейлора:
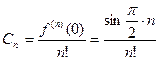 . Пусть
. Пусть 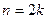 , тогда
, тогда 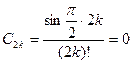 , если
, если 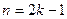 , то
, то 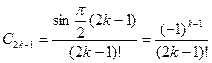 так как
так как 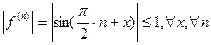 , то по теореме 2, можно утверждать, что ряд Тейлора сходится к функции
, то по теореме 2, можно утверждать, что ряд Тейлора сходится к функции 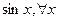 .
.
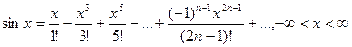 .
.
Функция 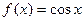 . Можно провести аналогично разложение, а можно разложить другим способом. Мы знаем, что степенной ряд можно дифференцировать в интервале его сходимости. Тогда
. Можно провести аналогично разложение, а можно разложить другим способом. Мы знаем, что степенной ряд можно дифференцировать в интервале его сходимости. Тогда 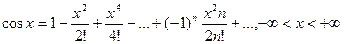 .
.
Ряд Маклорена для функции 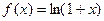 .
.
Так как функция 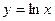 и ее производные не определены в точке
и ее производные не определены в точке 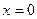 , поэтому будем рассматривать функцию
, поэтому будем рассматривать функцию 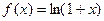 , которая определена
, которая определена 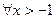 , вместе с производными. Продифференцируем
, вместе с производными. Продифференцируем 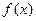 :
:
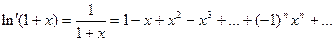
 - как сумма бесконечно убывающей геометрической прогрессии
- как сумма бесконечно убывающей геометрической прогрессии 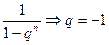 (имеет сумму при
(имеет сумму при 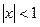 ).
).
Проинтегрируем этот ряд почленно по любому отрезку от  до
до 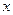 , где
, где 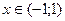 . Получим
. Получим 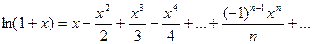 он сходится при
он сходится при 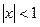 . Проверим сходится ли ряд на границах интервала
. Проверим сходится ли ряд на границах интервала 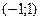 :
:
при 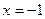 ряд вообще суммы не имеет, при
ряд вообще суммы не имеет, при 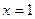 получается знакочередующийся ряд
получается знакочередующийся ряд 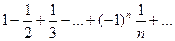 по теореме Лейбница он сходится, покажем, что он сходится к
по теореме Лейбница он сходится, покажем, что он сходится к 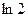 , то есть
, то есть 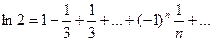 . Воспользуемся теоремой (достаточным условием разложимости в ряд Тейлора). Для этого оценим остаточный член в формуле Лагранжа.
. Воспользуемся теоремой (достаточным условием разложимости в ряд Тейлора). Для этого оценим остаточный член в формуле Лагранжа. 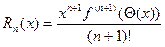 при
при 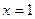
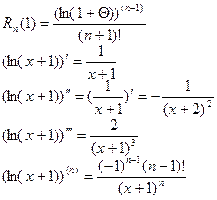 Тогда
Тогда 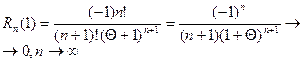 .
.
Таким образом,  , то есть ряд сходится при
, то есть ряд сходится при 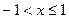 .
.
При 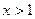 ряд расходится, так как не выполнено необходимое условие сходимости ряда, так как
ряд расходится, так как не выполнено необходимое условие сходимости ряда, так как 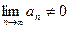 .
.
Дата публикования: 2015-07-22; Прочитано: 525 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
