Коррелатный способ уравнивания

Приведенная выше система уравнений (14.8) имеет нелинейный вид. В математике не существует способов решения таких систем нелинейных уравнений. В связи с этим данную систему уравнений раскладывают в ряд Тейлора, ограничиваясь только первыми членами разложения с учетом того, что значения поправок v_i достаточно малы (на основании выдержанных при измерениях допусков по точности), и вторые их степени будут весьма малыми, так что ими можно будет пренебречь. В результате уравнения (14.8) преобразуются к виду:

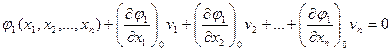
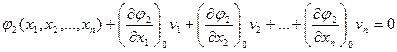(14.78)

……………………………………………………..

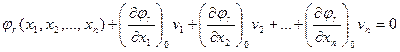
Введем обозначения:

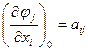(i = 1, 2, …, n; j = 1, 2, …, r), (14.79)

где i – номер измеренной величины (х); j – номер условного уравнения(илифункции φ).

С учетом введенных обозначений получим:

а₁₁v₁ + a₂₁v₂ + … + a_n1v_n + W₁ = 0

а₁₂v₁ + a₂₂v₂ + … + a_n2v_n + W₂ = 0 (14.80)

……………………………………

а_1rv₁ + a_2rv₂ + … + a_nrv_n + W_r = 0

В обозначениях гауссовых сумм:

[ a₁v ] + W₁ = 0

[ a₂v ] + W₂ = 0 (14.81)

………………

[ a_rv ] + W_r = 0

Равенства (14.80) и (14.81) называются условными уравнениями поправок.

Следует иметь в виду, что формулы (14.79) не используются, если известно, что система уравнений (14.8) имеет линейный вид, т.е. коэффициенты a_ij известны.

Для решения задачи уравнивания способом Лагранжа необходимо составить следующую функцию:

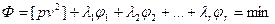, (14.82)

где 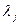- неопределенные множители Лагранжа.

Обозначим: 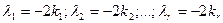, где - коррелаты. Тогда функцию (14.82) можно записать со значениями коррелат:

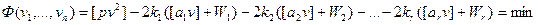. (14.83)

Для определения поправок v_i, при которых функция (14.83) достигает минимума, найдем частные производные по аргументам v_i и приравняем их нулю:

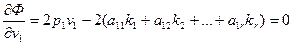
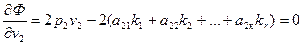(14.84)

………………………………………..

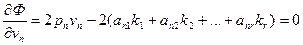
Из полученной системы уравнений следует, что

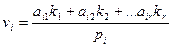(i= 1, 2, …, n) (14.85)

или

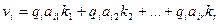, (14.86)

где 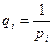- обратный вес измерения с индексом i.

Уравнения (14.85) и (14.86) называют коррелатными уравнениями поправок.

Число коррелат всегда равно числу условий. В результате образуется система коррелатных уравнений поправок v_i, содержащая n неизвестных поправок v_i и r неизвестных коррелат k_j, состоящая из n линейных уравнений.

Опуская промежуточные, хотя и важные преобразования (вывод можно посмотреть в соответствующей геодезической литературе), основанные на методе наименьших квадратов, приведем т.н. нормальные уравнения коррелат, в которых число неизвестных равно числу уравнений:

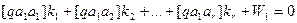
(14.87)

…………………………………………

………………………………………….

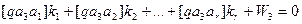
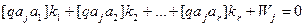
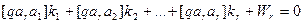
В уравнениях (14.87) неизвестными являются коррелаты k_i, а свободными членами – свободные члены уравнений поправок (14.80) и (14.81).

Как видно, при каждом параметре (неизвестном) k_i в уравнениях (14.87) стоит коэффициент в виде гауссовой суммы. Представим указанные коэффициенты в развернутом виде с помощью таблицы коэффициентов уравнений поправок (табл. 14.3).

Развернутый вид коэффициентов 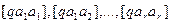, в которых индекс при коэффициентах а – это второй индекс коэффициентов условных уравнений поправок:

Таблица 14.3

Матрица коэффициентов линейных уравнений

i   j				…	i	…	n
	a11	a21	a31	…	ai1	…	an1
	a12	a22	a32	…	ai2	…	an2
	a13	a23	a33	…	ai3	…	an3
…	…	…	…	…	…	…	…
j	a1j	a2j	a3j	…	ajj	…	anj
…	…	…	…	…	…	…	…
r	a1r	a2r	a3r	…	ajr	…	anr
qi	q1	q2	q3	…	qi	…	qn

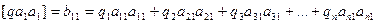
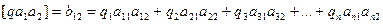
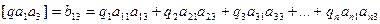
……………………………………………… (14.88)

………………………………………………

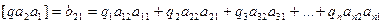
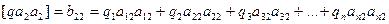
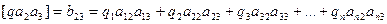
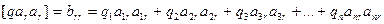
Рассмотрим подробнее принцип вычисления коэффициентов b_jj при коррелатах k_j в нормальных уравнениях коррелат.

1-е уравнение коррелат.

Коэффициент при k ₁ равен сумме произведений обратных весов и квадратов коэффициентов первой строки матрицы.

Коэффициент при k₂ равен сумме произведений обратных весов и коэффициентов 1-й и 2-й строк матрицы.

Далее производятся последовательные действия для всех остальных строк до последней строки. Так, коэффициент при k_r равен сумме произведений обратных весов и коэффициентов 1-й и r -й строк матрицы.

2-е уравнение коррелат.

Коэффициент при k₁ равен сумме произведений обратных весов и коэффициентов 2-й и 1-й строк матрицы.

Коэффициент при k₂ равен сумме произведений обратных весов и квадратов коэффициентов 2-й строки матрицы.

Коэффициент при k₃ равен сумме произведений обратных весов и коэффициентов 2-й и 3-й строк матрицы и т.д. до последней строки.

Аналогично выполняются вычисления для остальных строк.