 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Литературный обзор
|
|
Оглавление
Литературный обзор………………………………………3 стр.
Постановка задачи…………………………………………9 стр
Вывод основных уравнений……………………………….11 стр
Расчет колебаний пузырька при разных модах и начальных радиусах……………………………………………………..16 стр
Литературный обзор
Впервые задача об устойчивости плоской границы раздела между двумя жидкостями различной плотности была поставлена и решалась Дж. Тейлором, который показал, что граница раздела устойчива или неустойчива в зависимости от того, направлено ли ускорение от более плотной жидкости к менее плотной и наоборот. В дальнейшем эта задача подвергалась более детальному исследованию, поскольку условия устойчивости, выведенные Тейлором, не могли дать полного объяснения в случае, когда граница раздела имеет сферическую форму. Одним из первых, кто это сделал, был Плессет который в своей классической работе рассмотрел задачу об устойчивости границы раздела между двумя несмешивающимися несжимаемыми жидкостями разной плотности при радиальном движении. Проблему устойчивости он ограничил искажением сферической границы раздела малой амплитудой. При выводе уравнений возмущенный радиус пузырька разлагался в ряд по поверхностным сферическим гармоникам Yn где нулевой член ряда a-это радиус невозмущенной границы раздела, а коэффициент при гармонике порядка п ап-это амплитуда возмущения поверхности соответствующей модой. Из основных гидродинамических уравнений, с учетом только членов до первого порядка малости по амплитуде возмущения, Плессетом была получена система дифференциальных уравнений на невозмущенную границу раздела R и на амплитуду возмущения границы раздела ап. В полученных уравнениях амплитуда возмущения не влияет на уравнение движения для невозмущенной границы раздела, которое в случае, когда внутри сферы находится газ (то есть его плотностью по сравнению с плотностью жидкости можно пренебречь), есть не что иное, как уравнение Рэлея-Ламба, а также не зависит от амплитуд возмущений других мод.
Далее Плессет в своей работе исследует устойчивость сферической формы пузырька, проводя анализ на основе выведенных уравнений. Для этого уравнение на амплитуду возмущения с помощью подстановки сводится к виду уравнения Хилла, для которого известны критерии устойчивости. Получено, что в случае отсутствия поверхностного натяжения неустойчивость, аналогичная неустойчивости Тейлора, имеет место при положительном ускорении сферического радиуса пузырька. Кроме того, при отрицательном ускорении также возможна неустойчивость, когда давление газа больше по сравнению с давлением жидкости. В работе Плессета совместно с Митчелом исследуется неустойчивость сферической поверхности раздела при знакопостоянном ускорении, направленном к центру пузырька, то есть рассматривается только расширение или схлопывание пузырька. В этом случае граница раздела устойчива по Тейлору, но амплитуды возмущения границы раздела зависят от радиуса пузыря a как a -1/4 и захлопывающаяся полость оказывается неустойчивой. Кроме того, в данной работе показано, что поверхностное натяжение при схлопывании пузырька уменьшает возможность появления данной неустойчивости. Чуть раньше подобные результаты были получены, но другим способом Биркгофом, поэтому данная неустойчивость в литературе называется неустойчивостью Биркгофа-Плессета. В работе выводятся более общие условия устойчивости. В работе Воинова, Перепелкина при исследовании устойчивости поверхности сферического газового пузыря, совершающего нелинейные колебания в жидкости, сравнивались вышеупомянутые два вида неустойчивостей (Тейлора и Биркгофа-Плессета). Здесь анализ устойчивости был ограничен рассмотрением коротковолновых возмущений. Один из основных результатов, полученных в данной работе состоит в выводе, что главной причиной разрушения поверхности пульсирующего газового пузыря является неустойчивость Тейлора, в то время как неустойчивость Биркгофа-Плессета менее значительна.
В приведенных работах анализ устойчивости поверхности пузыря основывался непосредственно на уравнениях, выведенных Плессетом, тогда как в следующей группе работ этот анализ базировался на линеаризованных уравнениях на радиус невозмущенного пузырька и на амплитуду возмущения. В работе исследовались два типа неустойчивости колеблющихся сферических пузырьков, подвергающихся воздействию акустического поля: неустойчивость положения пузырька в стоячей акустической волне, вызывающая беспорядочное «танцующее» движение пузырька и неустойчивость сферической поверхности пузырька, колеблющегося в акустическом поле. При этом утверждалось, что танцующее движение захваченного пузырька вызвано осцилляциями поверхности, которые параметрически возбуждаются колебаниями пузырька. Это выводилось из хорошего согласования между измеренными порогами для «танцующего» движения пузырька и рассчитанными порогами для неустойчивых колебаний поверхности. До этого подобное заключение также было сделано в работах Страсберга и Бенджамина. В работе исследовалась диффузия газа из пузырька в жидкость и наоборот. Было получено, что сферические газовые пузырьки в жидкости действием осциллирующего поля давления неограниченно растут. Однако это поведение экспериментально не наблюдалось. В связи с этим и возникает вопрос об устойчивости сферического пузырька в осциллирующем поле давления. При подстановке данного решения в уравнения на амплитуду возмущения получалось уравнение Матье, коэффициенты которого зависят от параметра A. Полученное уравнение затем исследовалось для определения порога неустойчивости. В работахучитывались члены только до первого порядка по параметру А, а нелинейные члены отбрасывались.
В вышеприведенных работах жидкость считалась идеальной и поэтому эффекты вязкости не брались во внимание. В следующей группе работ основное направление исследований было посвящено включению вязкости в рассмотрение и выводу соответствующих уравнений. Впервые вывод уравнений, аналогичных уравнениям Плессета, но с учетом вязкости, провел Просперетти. Сложность решения данной проблемы заключается в том, что вязкость является причиной образования вихрей вблизи стенки пузырька и задача становится нелокальной по времени, поскольку с помощью конвективных и диффузионных процессов вихри рассеиваются по всей жидкости. Полученные в работе полные гидродинамические уравнения имеют громоздкий вид и не удобны для проведения дальнейших исследований, в связи с этим возникла идея несколько ограничить решение и аппроксимировать эти уравнения. Это было проделано, где было показано, что для малых значений вязкости образующиеся вихри могут быть локализованы. Была представлена аппроксимация нелокальных уравнений Просперетти в предположении, что течение жидкости происходит только в тонком пограничном слое вокруг пузырька.
На основе полученных аппроксимированных уравнений для несферических колебаний пузырька, учитывающих вязкость жидкости, в работе исследовались воздушные пузырьки, пульсирующие под действием осциллирующего акустического поля. Анализ проводился с учетом двух механизмов неустойчивости: уже упоминавшейся неустойчивости Рэлея-Тейлора и параметрической неустойчивости. Последняя имеет место, когда система за много периодов колебаний накапливает возмущения поверхности, что и приводит к разрушению пузырька. В работе к этим двум видам неустойчивости добавляется для анализа также и, так называемая, неустойчивость после отскока (afterbounce instability) пузырька, которая развивается параметрически во время быстрых отскоков, появляющихся у пузырьков после достижения минимального радиуса. Этот тип неустойчивости аналогичен параметрической неустойчивости, но отскоки не строго периодичны. Эти три типа неустойчивостей отличаются различными временными отрезками, на которых они действуют. Главное заключение, которое делается, состоит в следующем. При больших амплитудах внешнего давления только пузырьки с очень маленьким начальным радиусом устойчивы, как для неустойчивости Рэлея-Тейлора, так и для параметрической неустойчивости. Для жидкостей малой вязкости на пузырек начинает действовать параметрическая неустойчивость, чье время действия сравнимо с временем действия диффузии (~ 10-3 с). Это позволяет пузырьку восстановить свой радиус посредством диффузии через несферическую поверхность и, таким образом, переопределить область параметров устойчивости, что «защищает» пузырек от попадания в область действия неустойчивости Рэлея-Тейлора. В высоко вязких жидкостях пузырек раньше уничтожится неустойчивостью Рэлея-Тейлора, которая действует быстро (~ 10-9 с), чем попадет в устойчивую область параметрического пространства (это одно из объяснений, почему не была обнаружена сонолюминесценция в высоко вязких жидкостях). Однако, следует заметить, что выводы для высоко вязких жидкостей, на основе аппроксимированных уравнений, делать нельзя, поскольку они выводились из предположения малой вязкости.
В работе представлено сравнение аппроксимации работы и точных уравнений при исследовании областей параметрической неустойчивости. Естественно, что более точное решение будет получаться из полной системы уравнений. Однако один из основных плюсов для использования аппроксимированных уравнений состоит в том, что для них легче находить пороги неустойчивости, поскольку для этого существует соответствующий математический аппарат, тогда как для полных
интегро-дифференциальных уравнений приходится прибегать к интегрированию
по многим циклам для каждого конкретного случая, чтобы определить устойчива или неустойчива поверхность пузырька. Сравнение устойчивых областей, вычисленных по уравнениям показало, что для малых амплитуд внешнего давления эти области практически совпадают. При более высоких амплитудах полная модель немного более устойчива, чем ее аппроксимация.
В работе, в отличие от предыдущих работ, предлагается подход, при котором в ряд по сферическим гармоникам разлагается не радиус, а объем пузырька, находящегося в несжимаемой слабо вязкой жидкости под действием сильного акустического поля. Были получены линейные уравнения движения для амплитуд сферических гармоник. На основе полученных уравнений исследовалось влияние температуры воды на устойчивые колебания пузырька. Было показано, что с увеличением температуры, колебания становятся менее устойчивыми.
Другое направление в исследовании несферических колебаний пузырьков связано с развитием нелинейных теорий для амплитуд возмущения, тогда как предыдущие исследования были основаны на линейной теории Плессета. Лонгует-Хиггинс в своей работе показал, что в нелинейной теории поверхностных колебаний пузырька амплитуда возмущения во втором порядке производит монопольное излучение звука, частота которого вдвое больше частоты пузырька при линейных колебаниях поверхности и амплитуда пропорциональна квадрату амплитуды отклонения поверхности пузырька от своей сферической формы. В линейной же теории, учитывающей амплитуду искажения только до первого порядка, производится незначительное излучение звука. В своей работе он показал, что для заданного начального искажения поверхности (без начального искажения объема) возможно разложение на нормальные моды, каждая из которых излучает независимо. Здесь включены различные механизмы диссипации (акустическая, термическая и вязкая), что ограничивает амплитуду сферической моды даже при частоте, точно совпадающей с резонансной. Из-за диссипации и наличия резонанса между сферической модой и модами искажений, частота пульсации звука, произведенного начальными возмущениями, приблизительно совпадает с частотой сферической моды. В работе показано, что преобладающим эффектом при колебании поверхности является не перенос энергии между модами около резонанса, а наоборот, затухание, которое возникает, главным образом, из акустического излучения и тепловой диффузии.
Бенджамин и Эллис исследовали неустойчивые движения маленьких пузырьков в жидкости, подвергающихся акустическим стоячим волнам. Продолжая исследования, они получили формулу для скорости дрейфа колеблющегося пузырька как следствие взаимодействия второго порядка между двумя соседними модами возмущения. Авторы данной работы указали, что полином Лежандра первого порядка описывает возмущение сферы, которое соответствует трансляционному движению пузырька. Его включение обеспечивает возможный механизм для явления дрейфа. В работе показано, что этот механизм может вызвать хаотический процесс. В работе исследовалось резонансное взаимодействие между модой радиальных колебаний и одной или двумя модами искажений колеблющихся пузырьков в воде, когда радиальная мода инициирована окружающим звуком с помощью несколько измененной теории Лонгует-Хиггинса. Было найдено численное доказательство появления хаотических колебаний пузырьков при простом гармоническом воздействии из-за взаимодействия одной или двух поверхностных мод. Авторы данной работы утверждают, что этот результат вместе с теорией Бенджамина и Эллиса обеспечивает один механизм для объяснения хаотического «танцующего» движения пузырьков в звуковом поле.
В работе рассматривались малые амплитуды колебания поверхности газового пузырька как под действием импульса давления, так и изменения давления скачком в начальный момент времени, при наличии и отсутствии осредненного течения. В анализ были включены амплитуды возмущения до второго и более высоких порядков малости. Заключения данной работы, в случае отсутствия течения, аналогичны теории Лонгует-Хиггинса, но качественные детали сильно зависят от начальных условий, то есть от того, имеет ли место начальная деформация, благодаря импульсу давления, скачку давления или просто налагается на неподвижную жидкость (как в случае Лонгует-Хиггинса). Показано, что наличие или отсутствие окружающего внешнего течения сильно влияют на природу взаимодействия между модами радиальных и поверхностных колебаний и на их величины. Так, например, показано, что течение может непосредственно взаимодействовать с модами искажения, усиливая перенос энергии при резонансе от поверхностных к радиальным колебаниям, что в итоге приводит к изменению частот колебаний.
Фэнг и Лил в своих работах также исследовали динамику пузырька, когда объемная мода колебаний связана с одной или двумя модами через квадратичный резонанс. В первом рассматривались колебания изначально возмущенного пузырька в идеальной жидкости, не подвергающегося воздействию давления, зависящего от времени. Здесь был рассмотрен механизм переноса энергии, благодаря резонансным взаимодействиям поверхности пузырька и объемным деформациям. Было найдено, что неустойчивость малых объемных колебаний может привести к большим колебаниям поверхности. Добавление возмущенного периодического давления любой амплитуды в невязкую систему, может привести к потере устойчивости объемной моды и, как следствие этой неустойчивости, к хаотическим колебаниям как объемной, так и поверхностной моды. Если ввести в систему хотя бы небольшую диссипацию, вызванную вязкостью, то хаотическая динамика будет реализована при достаточно больших амплитудах внешнего давления.
Постановка задачи
В равновесном состоянии одиночный газовый пузырек в безграничной идеальной несжимаемой жидкости плотности 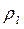 имеет сферическую форму радиуса
имеет сферическую форму радиуса 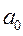 . Под действием изменения давления в жидкости пузырек начинает колебаться около своего начального положения. Допускается при этом нарушение сферической симметрии. Предполагается, что массовые силы отсутствуют и давление газа внутри пузырька изменяется адиабатически.
. Под действием изменения давления в жидкости пузырек начинает колебаться около своего начального положения. Допускается при этом нарушение сферической симметрии. Предполагается, что массовые силы отсутствуют и давление газа внутри пузырька изменяется адиабатически.
Для идеальной жидкости имеет место потенциальное течение при определенных условиях. Из теоремы Томпсона следует, что если в некоторый момент времени движение жидкости потенциально, то оно будет потенциальным и в течение всего дальнейшего времени. В частности, любое движение, возникшее из состояния покоя, потенциально. Но при этом, кроме выполнения условий теоремы Томпсона, необходимо потребовать также, чтобы выполнялось условие не нарушения непрерывности поля скоростей, т.к. при наличии разрыва скорости, при дальнейшем движении (из состояния покоя) в потоке могут появиться замкнутые контуры, по которым циркуляция будет отличаться от нуля.
Для потенциального течения несжимаемой жидкости из уравнения неразрывности получается уравнение Лапласа для потенциала скорости 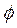 :
:
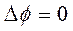
Решение данного уравнения выражается в сферических функциях, использующихся в случаях, когда граничные условия отнесены к сферическим (или близким к сферическим) поверхностям. В данной работе рассматриваются именно такие поверхности. В сферических координатах (r,  ),с началом отсчета в центре пузырька, уравнение имеет вид.
),с началом отсчета в центре пузырька, уравнение имеет вид.
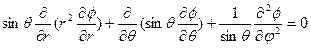
Решение этого уравнения, ограниченное во всей области, занятой жидкостью, можно записать в виде
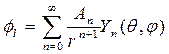 ,
,
а для области, занятой газом –
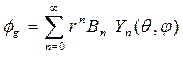 ,
,
где Yп(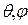 ) — поверхностная сферическая гармоника порядка п, которая является решением дифференциального уравнения
) — поверхностная сферическая гармоника порядка п, которая является решением дифференциального уравнения
 .
.
В случае, когда нет зависимости от угла 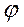 , функции Yn(
, функции Yn( ) выражаются через полиномы Лежандра Рп (cos
) выражаются через полиномы Лежандра Рп (cos 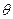 ) следующим образом
) следующим образом
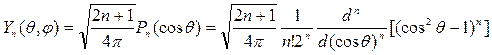 .
.
Тогда потенциал скорости жидкости примет вид
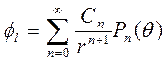 ,
,
Приведем формулы для функции Yn( ) при некоторых значениях п:
) при некоторых значениях п:
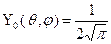 ,
,
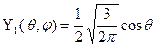 ,
,
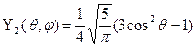 ,
,
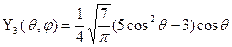 ,
,
 .
.
Дата публикования: 2015-07-22; Прочитано: 234 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
