Определение надежности и качества систем

Во многих случаях целью анализа является оценка характеристических свойств систем. К таким свойствам относятся, в частности, надежность и качество системы. Поэтому материал этого раздела тесно связан с тематикой предыдущего раздела.

Оценка надежности функционирования систем использует понятие структурной функции. Определение структурной функции системы, принятое в теории надежности, использует соотношения теории вероятностей. Мы применим для представления структурных функций теорию нечетких множеств, что значительно облегчит выполнение расчетов и делает их более наглядными. Введем бинарные переменные , , ,…, каждая из которых принимает лишь два значения {0;1}, и определим для них две операции: умножение () и кооперативное (ограниченное) суммирование ()

(6.3.1)

. (6.3.2)

Структурная функция системы определяется применением к переменным , , ,… операций и . Она имеет вид

. (6.3.3)

Например,

. (6.3.4)

Каждой структурной функции соответствует графическое представление системы, в котором параллельному соединению компонентов (элементов) соответствует операция , а последовательному – операция . Так, функции (6.3.4) соответствует схема, состоящая из трех параллельных компонентов. Первый компонент состоит из элемента , второй компонент – из последовательно соединенных и ; третий – из последовательно соединенных элементов и . Мы не будем использовать графическое представление, ввиду его громоздкости, и ограничимся словесным описанием, которое вполне понятно.

Обычно для представления структурной функции используется каноническая (приведённая) форма, которая имеет наиболее простой вид и не содержит степеней и подобных членов (аналогично многочленам в алгебре). Для упрощения структурных функций используются свойства поглощения

, (6.3.5а)

. (6.3.5б)

Соотношения (6.3.5а), (6.3.5б) эквивалентны. Поясним их действие примером. Каноническая форма функции (6.3.4) имеет вид

, (6.3.4а)

так как по (6.3.5б) имеем . Рассмотрим в качестве примера систему, структурная функция которой имеет вид

. (6.3..6)

Из (6.3.6) следует, что система состоит из четырех параллельных компонентов , , , и , причем первый компонент содержит два последовательных элемента и , второй – и , третий – один элемент , четвертый – три последовательных элемента , и . Применяя свойство (6.3.5б), получаем каноническую форму в виде

, (6.3.6а)

так как и .

Чтобы оценить надёжность системы по структурной функции, сопоставим каждому аргументу этой функции состояние компонента (элемента) системы. Будем считать, что, например, компонент функциональный, если соответствующая ему бинарная переменная (аргумент) , и не функциональный, если . В этом случае, очевидно, что структурная функция также является бинарной и принимает значения {0;1}. Система 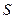функциональная (т.е. безотказно работает), если её структурная функция , и нефункциональная (т.е. не работает), если . Так как надежность системы определяется через вероятности безотказной работы ее компонентов, то нужно перейти от переменных , , ,… к вероятностям , , и т.д., где – вероятность того, что компонент функциональный и т.д. Обозначим вероятность, что система 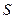функциональная, т.е. надежность системы, как . Между структурной функцией и вероятностью имеется взаимнооднозначное соответствие (изоморфизм). Удобство использования функции в том, что для операций и выполняется свойство идемпотентности («равномощности»), которое имеет вид

, (6.3.7)

. (6.3.8)

Для обычного сложения , и сумма выходит за пределы {0;1}, поэтому ее нельзя сопоставить вероятности. Для того чтобы перейти от к нужно в заменить операцию на обычное сложение согласно (6.3.2), затем, применяя для упрощения свойства идемпотентности (6.3.7), (6.3.8), избавиться от степеней, и, наконец, перейти к вероятностям, заменяя на , на и т.д. Таким образом, надежность системы определяется структурной функцией, в которой аргументами являются вероятности функциональности отдельных компонентов системы, связанные обычными операциями сложения и умножения. Мы можем записать

, (6.3.9)

где – приведенная структурная функция системы. Проиллюстрируем это на примере системы, представленной (6.3.6а). Переходим к обычной операции сложения, что дает

. (6.3.10)

Поскольку все переменные входят в первой степени, то сразу получаем, заменяя на и т.д.

. (6.3.11)

Выражение (6.3.11) можно преобразовать, вводя вероятность отказа , но мы не будем этим заниматься, ввиду очевидности преобразований. Изложенный подход применяется к техническим системам. Однако для сложных интеллектуальных систем, а также при теоретическом анализе технических систем удобно использовать нечеткий подход. Действительно, в первом случае числовая оценка надежности часто не может быть выполнена. Например, оценка надежности человека или предприятия величиной 90% мало о чем говорит. Во втором случае, т.е. при теоретическом анализе, часто бывает необходимо оперировать оценками, не зависящими от контекста. При нечетком подходе представим надежность системы в виде нечеткой переменной. Тогда выражение (6.3.9) преобразуется к виду

, (6.3.12)

где все величины являются нечеткими, и операции выполняются с нечеткими величинами. Результат получается в виде функции принадлежности , описывающей нечеткую величину . Для представления удобно использовать нечеткие градации, например, ОВ, В, С, Н, ОН (см. ниже). В этом случае вычисления упрощаются. Для этого достаточно заметить, что при выполнении операции умножения значение произведения сдвигается в меньшую сторону на одну градацию относительно наименьшей градации сомножителей, так как операция является наибольшей операцией пересечения (). При перемножении трех величин происходит сдвиг в меньшую сторону на две градации и т.д. Очевидно, что если достигнута наименьшая градация (в нашем случае ОН или ООН), то дальнейшее умножение ничего не дает. Например, если и , то . При выполнении операции суммирования, наоборот, происходит сдвиг суммы двух нечетких величин в большую сторону на одну градацию относительно наибольшей градации слагаемых, так как операция больше операции . При суммировании трех величин происходит сдвиг в большую сторону на две градации и т.д. Очевидно, что если достигнута наибольшая градация (в нашем случае ОВ или ООВ), то дальнейшее сложение ничего не дает. Например, если , , то . В первом приближении для произведения нечетких величин, представленных нечеткими градациями, можно записать

(6.3.13а)

где – число градаций, на которое уменьшается минимум, равное числу нечетких сомножителей без единицы. При этом левая часть должна оставаться в пределах допустимых градаций. Аналогично для суммы нечетких величин в первом приближении запишем

, (6.3.13б)

где – число градаций, на которое увеличивается максимум, равное числу нечетких слагаемых без единицы. При этом левая часть должна оставаться в пределах допустимых градаций. Более точно результат можно оценить по таблицам [42].

Оценка качества функционирования системы может быть проведена на основе нечетких переменных. Будем описывать качество функционирования системы в виде нечетких градаций, например: очень-очень высокое значение (ООВ), очень высокое значение (ОВ), высокое (В), среднее (С), низкое (Н), очень низкое (ОН), очень-очень низкое, или не работает (ООН). Каждому компоненту системы 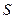соответствует то или иное значение нечеткой переменной , представленной нечеткими градациями. Для последовательного соединения компонентов функция, характеризующая качество функционирования системы, определяется свёрткой (операцией)

. (6.3.14)

Для параллельного соединения используется свёртка (операция)

. (6.3.15)

Для упрощения функций используются свойства поглощения

, (6.3.15а)

. (6.3.15б)

Кроме того операции , обладают свойствами идемпотентности и взаимной дистрибутивности

, (6.3.16а)

, (6.3.16б)

, (6.3.17а)

, (6.3.17б)

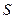где , , – нечетные переменные. Выражения (6.3.15а) – (6.3.17б) позволяют представить функцию в каноническом виде. Функция является показателем качества функционирования системы. Рассмотрим в виде примера систему , состоящую из двух последовательных компонентов и , причем компонент состоит из трех параллельных ветвей: первая ветвь содержит три последовательных элемента , и ; вторая – два последовательных элемента и ; третья состоит из одного элемента . Компонент состоит из одного элемента . Показатель качества функционирования системы имеет вид

, (6.3.18)

где , , – нечеткие переменные, связанные с элементами , , соответственно. Применяя правила поглощения и свойства дистрибутивности и идемпотентности, получаем

. (6.3.18а)

Чтобы провести расчет, предположим, что , , . Тогда из (6.3.18а) имеем

, (6.3.19)

т.е. качество функционирования системы – высокое. Отметим, что система не работает (нефункциональная), если не работает, или одновременно и не работают, или , и одновременно не работают. Следовательно, качество функционирования системы и её функциональность не тождественны друг другу. Чтобы это пояснить, рассмотрим систему 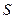, состоящую из двух последовательных компонентов. Для структурной функции имеем

. (6.3.20)

Для показателя качества функционирования получаем

. (6.3.21)

Надёжность системы 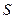равна , а качество функционирования . Если , то , т.е. надёжность системы при , может сильно уменьшиться по сравнению с надежностью отдельного компонента. В то же время качество функционирования остается в этом случае примерно на том же уровне. Если два компонента системы 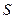соединены параллельно, то имеем

. (6.3.22)

В этом случае для надёжности получаем . Для показателя качества функционирования имеем . Если , то , т.е. надёжность системы увеличивается при по сравнению с отдельным компонентом, хотя и не слишком сильно. Для показателя качества при имеем , т.е. качество функционирования остается на том же уровне, что и для отдельного компонента.

Таким образом, при параллельном соединении двух систем или их частей (подсистем, компонентов, элементов) ни надёжность, ни качество функционирования не ухудшаются. При последовательном соединении систем ни надёжность, ни качество функционирования общей системы не улучшаются. При соединении близких по надёжности и качеству систем, тип соединения (последовательный или параллельный) гораздо сильнее сказывается на надежности, особенно, если надёжность соединяемых систем мала. В то же время качество функционирования практически остается на том же уровне.