 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Предельные теоремы теории веротностей
|
|
Теория вероятностей изучает закономерности, свойственные массовым случайным явлениям. Если явление носит единичный характер, теория вероятностей способна обычно предсказать лишь результаты в очень широких пределах. Закономерности проявляются именно при большом числе случайных явлений, происходящих в однородных условиях. При этом характеристики случайных величин, наблюдаемых при испытании, становятся устойчивыми. Например, устойчива частота появления события при большом числе испытаний, то же относится и к средним значениям случайных величин.
Группа теорем, устанавливающих соответствие между теоретическими и экспериментальными характеристиками случайных величин и случайных событий при большом числе испытаний над ними, носит название предельных теорем теории вероятностей. К ним относятся Закон больших чисел (группа теорем, включающая, в частности, неравенство Маркова, неравенство и теорему Чебышева, теорему Бернулли) и Центральная предельная теорема Ляпунова.
Неравенство Маркова. Для положительных случайных величин, имеющих математическое ожидание, справедливо неравенство Маркова (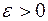 ):
): 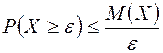 . Неравенство Маркова в первоначальной форме или в форме
. Неравенство Маркова в первоначальной форме или в форме 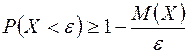 применяют для оценки вероятности положительных случайных величин с неизвестным законом распределения.
применяют для оценки вероятности положительных случайных величин с неизвестным законом распределения.
Неравенство Чебышева. Пусть случайная величина Х имеет математическое ожидание 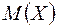 и дисперсию
и дисперсию 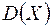 . Вероятность того, что отклонение случайной величины от ее математического ожидания будет по абсолютному значению не меньше любого положительного числа
. Вероятность того, что отклонение случайной величины от ее математического ожидания будет по абсолютному значению не меньше любого положительного числа 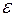 , ограничена сверху величиной
, ограничена сверху величиной 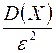 , то есть:
, то есть:  или
или 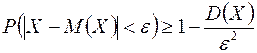 .
.
Теорема Чебышева. Если 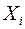 (i= 1; 2; 3; …; п) – попарно-независимые случайные величины с математическими ожиданиями
(i= 1; 2; 3; …; п) – попарно-независимые случайные величины с математическими ожиданиями 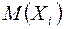 и дисперсиями
и дисперсиями 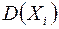 , ограниченными одной и той же постоянной С, то для любого
, ограниченными одной и той же постоянной С, то для любого 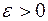 :
:
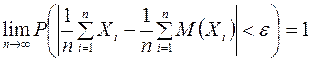 .
.
Справедлива также оценка:
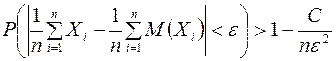 .
.
Следствие. Если в условии теоремы Чебышева случайные величины имеют одинаковые распределения, то есть 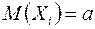 ;
; 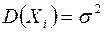 , то
, то
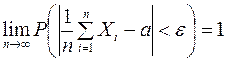 и
и 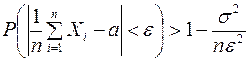 .
.
Теорема Бернулли. Пусть т – количество наступлений события А в серии из п независимых испытаний; р – вероятность наступления события А в одном испытании. Тогда для любого 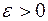 :
:
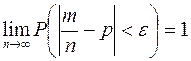 и
и 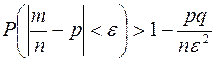 .
.
Центральная предельная теорема Ляпунова. Теорема показывает, что при достаточно большом числе п независимых случайных величин Х 1, Х 2, …, Хп, подчиненных каким угодно законам распределения (при соблюдении некоторых ограничений), их сумма будет иметь закон распределения, как угодно близкий к нормальному закону.
Теорема. Если случайные величины Х 1, Х 2, …, Хп взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием а и дисперсией 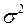 , то при неограниченном увеличении п закон распределения суммы этих случайных величин
, то при неограниченном увеличении п закон распределения суммы этих случайных величин 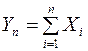 неограниченно приближается к нормальному.
неограниченно приближается к нормальному.
В практических задачах часто применяют центральную предельную теорему для определения вероятности того, что сумма нескольких случайных величин окажется в заданных пределах.
Примеры:
1. При стрельбе по мишени, представляющей собой круг 30 см, средняя величина отклонения от центра мишени равна 6 см. Оцените вероятность поражения мишени при одном выстреле.
Решение. По условию задачи 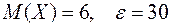 . Применяя неравенство Маркова, получим:
. Применяя неравенство Маркова, получим: 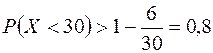 .
.
2. Среднее значение длины спички равно 4 см, а среднее квадратическое отклонение 0,2 см. Оцените вероятность того, что длина наугад взятой спички окажется не менее 3,5 см и не более 4,5 см.
Решение. По условию задачи 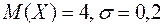 . Так как длина спички колеблется от среднего значения
. Так как длина спички колеблется от среднего значения 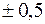 , то
, то 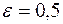 . Воспользуемся неравенством Чебышева
. Воспользуемся неравенством Чебышева 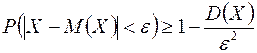 , где
, где 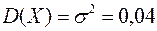 . Тогда получим:
. Тогда получим:
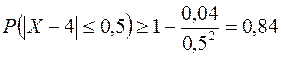 .
.
3. Оцените вероятность того, что бросив монету 200 раз относительная частота появления герба при одном испытании по абсолютной величине отклонится не больше чем на 0,1.
Решение. Из условия задачи 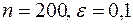 . Вероятность того, что появится герб при однократном бросании монеты, равна
. Вероятность того, что появится герб при однократном бросании монеты, равна 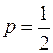 . Тогда
. Тогда 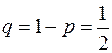 .
.
Воспользуемся теоремой Бернулли 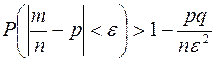 , тогда получим:
, тогда получим: 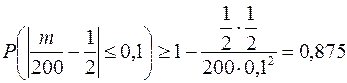 .
.
4. Для каждой из 2000 независимых с. в. Х 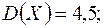
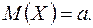 Оцените вероятность того, что среднее арифметическое случайных величин отклоняется от математического ожидания, а по абсолютной величине не более чем на 0,15.
Оцените вероятность того, что среднее арифметическое случайных величин отклоняется от математического ожидания, а по абсолютной величине не более чем на 0,15.
Решение. Воспользуемся следствием из теоремы Чебышева 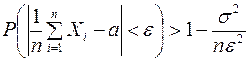 и данными из условия задачи
и данными из условия задачи 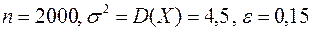 .
.
Тогда имеем: 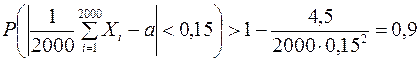 .
.
5. Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оцените вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом (математическим ожиданием) отказов за время Т окажется: а) меньше двух; б) не меньше двух.
Решение.
а) Пусть Х – число отказавших элементов за время Т. Тогда 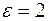 ,
, 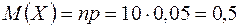 ,
,  .
.
Воспользуемся неравенством Чебышева:
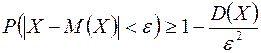 .
.
Тогда получим:  .
.
б) события 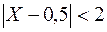 и
и 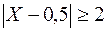 противоположны, поэтому сумма их вероятностей равна единице. Следовательно,
противоположны, поэтому сумма их вероятностей равна единице. Следовательно,
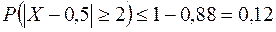 .
.
6. Норма высева на 1 га равна 150 кг. Фактический расход семян на 1 га колеблется около этого значения; случайные отклонения характеризуются средним квадратическим отклонением 10 кг. Определите: а) вероятность того, что расход семян на 100 га не превысит 15,1 т; б) количество семян, обеспечивающее посев 100 га с вероятностью 0,95.
Решение.
Обозначим через 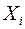 случайный расход семян на i -ом гектаре. По условию
случайный расход семян на i -ом гектаре. По условию  кг,
кг, 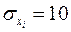 кг. Через Х обозначим расход семян на 100 га; этот расход равен сумме расходов каждого гектара:
кг. Через Х обозначим расход семян на 100 га; этот расход равен сумме расходов каждого гектара: 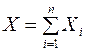 . На основании теоремы Ляпунова случайная величина Х будет распределена нормально. Параметры этого распределения таковы:
. На основании теоремы Ляпунова случайная величина Х будет распределена нормально. Параметры этого распределения таковы:
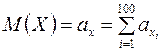 ;
; 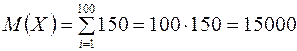 кг
кг 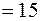 т;
т;
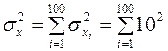 ,
, 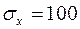 кг
кг 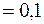 т.
т.
Теперь переходим к определению искомых величин:
а) воспользуемся формулой
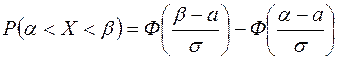 , (значения функции
, (значения функции 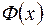 приведены в табл. А.2), получим:
приведены в табл. А.2), получим:
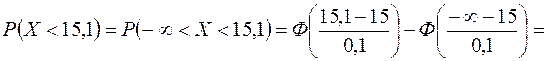
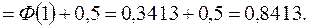
Таким образом, в заданных условиях вероятность того, что 15,1 т семян окажутся достаточными для засева 100 га, равна 0,841;
б) обозначим через 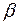 – количество семян, обеспечивающее посев с вероятностью 0,95, тогда справедливы соотношения
– количество семян, обеспечивающее посев с вероятностью 0,95, тогда справедливы соотношения 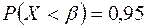 или
или 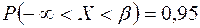 . Воспользуемся опять той же формулой
. Воспользуемся опять той же формулой 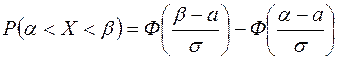 , тогда получим:
, тогда получим:
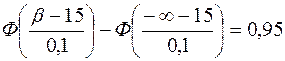 ;
;
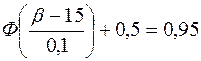 ;
; 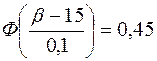 .
.
По табл. А.2 находим значение аргумента для полученного значения функции 0,45. Оно равно 1,64, тогда
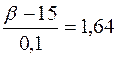 ;
; 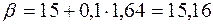 т.
т.
В заданных условиях 15,16 т семян обеспечат посев 100 га с вероятностью 0,95.
Дата публикования: 2015-07-22; Прочитано: 781 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
