 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Сложные учетные ставки
|
|
Рассмотрим антисипативный способ начисления сложного процента. Пусть
d  (%) - сложная годовая учетная ставка,
(%) - сложная годовая учетная ставка,
d  - относительная величина учетной ставки,
- относительная величина учетной ставки,
k - коэффициент наращения для случая учетной ставки,
f - номинальная годовая учетная ставка.
Тогда по прошествии первого года наращенная сумма по формуле (2.5) составит
 S
S 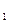 = P / (1 - d
= P / (1 - d  ), еще через год
), еще через год
S  = S
= S 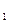 / (1 - d
/ (1 - d  ) = Р / (1 - d
) = Р / (1 - d  )
) 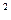 , и т.д.
, и т.д.
 По прошествии n лет
По прошествии n лет
S = P / (1 - d  )
)  (4.1).
(4.1).
Коэффициент наращения тогда
 k = 1 / (1 - d
k = 1 / (1 - d  )
)  (4.2).
(4.2).
Сравнивая формулы (3.1) и (4.1), можно увидеть, что при равенстве ссудного процента и учетной ставки наращение первоначальной суммы в случае антисипативного метода происходит быстрее. Поэтому часто можно столкнуться с утверждением, что декурсивный метод начисления более выгоден для заемщика, а антисипативный - для кредитора. Это справедливо лишь для невысоких процентных ставок, тогда расхождение не очень значительно. Но с ростом процентной ставки разница в величине наращенной суммы становится огромной и сравнение двух методов с точки зрения выгодности утрачивает смысл.
 Для периода начисления, не являющегося целым числом, имеем
Для периода начисления, не являющегося целым числом, имеем
k = 1 / ((1 - d  )
) 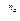
 (1 - n
(1 - n 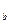
 d
d  )) (4.3)
)) (4.3)
 Для начисления процентов m раз в году формула наращенной суммы имеет такой вид
Для начисления процентов m раз в году формула наращенной суммы имеет такой вид
S = P / (1 - f/m) 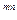 или
или
S = P / ((1 - f/m) 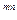
 (1 - l
(1 - l  f/m)), где
f/m)), где
mn -целое число интервалов начисления за весь период начисления, l - часть интервала начисления.
При непрерывном начислении процентов наращенная сумма рассчитывается по формуле
 S = P:
S = P: 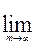 (1 - f/m)
(1 - f/m) 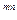
Из полученных формул путем небольших преобразований получим формулы для вычисления первоначальной суммы, срока начисления и величины учетной ставки:

P = S(1 - d  )
)  . n = (lnP/S) / ln(1-d
. n = (lnP/S) / ln(1-d  ). n = (lnP/S) / m ln(1-f/m).
). n = (lnP/S) / m ln(1-f/m).
d  = 1 -
= 1 - 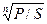 . f = m(1 -
. f = m(1 - 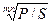 ).
).
В случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения различных процентных ставок, пользуются эквивалентными процентными ставками.
Эквивалентность процентных ставок различного типа.
Эквивалентные процентные ставки - это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты.
Для их нахождения используются уравнения эквивалентности, принцип составления которых заключается в следующем. Выбирается величина, которую можно рассчитать при помощи различных процентных ставок (обычно это величина наращенной суммы S). На основе равенства двух выражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида. Вспомним обозначения, использованные ранее
i -простая годовая ставка ссудного процента,
d - простая годовая учетная ставка,
i  - сложная годовая ставка ссудного процента,
- сложная годовая ставка ссудного процента,
d  - сложная годовая учетная ставка,
- сложная годовая учетная ставка,
j - номинальная ставка ссудного процента
f - номинальная учетная ставка
Запишем также известные нам формулы для определения наращенной суммы при различных способах начисления процентов:
 S = P
S = P  (1 + n
(1 + n  i) (1)
i) (1)
S = P/(1 - n  d) (2)
d) (2)
S = P  (1 + i
(1 + i  )
)  (3)
(3)
S 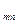 = P
= P  (1 + j/m)
(1 + j/m) 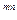 (4)
(4)
S = P/(1 - d  )
)  (5)
(5)
S = P/(1 - f/m) 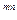 (6)
(6)
 Приравнивая эти формулы попарно, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками. Например, приравнивая (1) и (2), получим
Приравнивая эти формулы попарно, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками. Например, приравнивая (1) и (2), получим
1 + n  i = 1/(1-n
i = 1/(1-n  d), откуда
d), откуда
i = d/(1-n  d),
d),
d = i/(1 + n  i).
i).
Из формул (1) и (3) получаем
 1 + n
1 + n  i = (1 + i
i = (1 + i 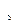 )
)  ,
,
i = ((1 + i 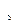 )
)  -1) / n,
-1) / n,
i 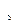 =
= 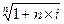 - 1.
- 1.
Из формул (1) и (4) получим
 1 + n
1 + n  i = (1 + j/m)
i = (1 + j/m) 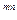 ,
,
i = ((1 + j/m) 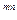 - 1) / n,
- 1) / n,
j = m(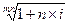 - 1).
- 1).
Аналогично можно получить зависимости между любыми другими эквивалентными процентными ставками. Для различных случаев сложных процентов получаем уравнение эквивалентности, приравнивая (3) и (4):
 (1 + i
(1 + i  )
)  =(1 + j/m)
=(1 + j/m) 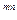 , откуда i
, откуда i  = (1 + j/m)
= (1 + j/m) 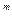 -1, j = m(
-1, j = m(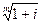
 - 1).
- 1).
В данном выражении i  - годовая ставка сложного процента, эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов. Она помогает оценить реальную доходность финансовой операции. При m=1 очевидно, что i
- годовая ставка сложного процента, эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов. Она помогает оценить реальную доходность финансовой операции. При m=1 очевидно, что i  = j.
= j.
Далее, приравнивая (3) и (5), получим
 (1 + i
(1 + i  )
)  = 1/(1 - d
= 1/(1 - d  )
)  , откуда i
, откуда i  = d/(1-d), d = i
= d/(1-d), d = i  /(1 + d).
/(1 + d).
Аннуитет.
В большинстве современных коммерческих операций подразумеваются не разовые платежи, а последовательность денежных поступлений (или выплат) в течение определенного периода. Это может быть серия доходов и расходов некоторого предприятия, выплата задолженностей, взносы для создание тех или иных фондов и т.д. Такая последовательность называется потоком платежей.
Поток однонаправленных платежей с равными интервалами между последовательными платежами в течение определенного количества лет называется аннуитетом (финансовой рентой).
Наиболее распространенные примеры аннуитетов - регулярные взносы в пенсионный фонд, погашение долгосрочного кредита, выплата процентов по ценным бумагам.
Поступления аннуитета можно обозначить следующим образом:
CF 1 = CF 2 = … = CF n = CF.
Аннуитеты могут между собой различаться по следующим характеристикам
- величиной каждого отдельного платежа,
- интервалом времени между двумя последовательными платежами (периодом аннуитета),
- сроком от начала аннуитета до конца его последнего периода (бывают и неограниченные по времени - вечные аннуитеты),
- процентной ставкой, применяемой при наращении или дисконтировании платежей.
По времени наступления платежей различают два вида аннуитета
1. обыкновенный аннуитет – когда платежи происходят в конце каждого периода – ПОСТНУМЕРАНДО.
2. авансовый аннуитет – тогда платежи происходят в начале каждого периода – ПРЕНУМЕРАНДО.
По продолжительности денежного потока различают:
1. Срочный аннуитет - денежный поток с равными поступлениями в течение ограниченного промежутка времени.
2. Бессрочный аннуитет - когда денежные поступления продолжаются достаточно длительного времени.
С практической точки зрения наибольший интерес представляют собой аннуитеты, в которых все платежи равны между собой (постоянные аннуитеты), либо изменяются с определенной закономерностью. Такие аннуитеты мы и рассмотрим.
Пусть
P - величина каждого отдельного платежа,
i  - сложная процентная ставка, по которой начисляются проценты,
- сложная процентная ставка, по которой начисляются проценты,
S 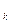 - наращенная (будущая) сумма для k-го платежа аннуитета постнумерандо,
- наращенная (будущая) сумма для k-го платежа аннуитета постнумерандо,
S - наращенная (будущая) стоимость всего аннуитета постнумерандо (сумма всех платежей с процентами),
A 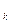 - современная (настоящая) величина k-го платежа аннуитета постнумерандо (сумма настоящих стоимостей всех платежей),
- современная (настоящая) величина k-го платежа аннуитета постнумерандо (сумма настоящих стоимостей всех платежей),
A - современная (настоящая) стоимость всего аннуитета постнумерандо (сумма настоящих стоимостей всех платежей),
Sп - наращенная сумма аннуитета пренумерандо,
Ап - современная величина аннуитета пренумерандо,
n - число платежей.
Рассмотрим аннуитет постнумерандо с ежегодными платежами Р в течение n лет, на которые начисляются проценты по сложной ставке i.
 Для первого платежа S
Для первого платежа S 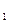 платежи будут начисляться (n-1) раз, тогда, согласно формуле (3.1) для сложных ставок ссудных процентов,
платежи будут начисляться (n-1) раз, тогда, согласно формуле (3.1) для сложных ставок ссудных процентов,
S 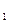 = Р (1 + i
= Р (1 + i  )
) 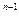 .
.
Для второго платежа S  (проценты на него будут начисляться на год меньше) -
(проценты на него будут начисляться на год меньше) -
 S
S  = Р (1 + i
= Р (1 + i  )
) 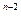 и т.д.
и т.д.
На последний платеж, произведенный в конце n-го года, проценты уже не начисляются, т.е.
 S
S 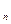 = Р.
= Р.
Тогда для общей наращенной суммы
 S =
S = 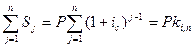 , (1)
, (1)
где k 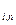 - коэффициент наращения аннуитета с параметрами i, n. Он является суммой членов геометрической прогрессии, для которой первый член a
- коэффициент наращения аннуитета с параметрами i, n. Он является суммой членов геометрической прогрессии, для которой первый член a 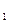 =1, а знаменатель равен (1+ i
=1, а знаменатель равен (1+ i  ) = q. Суммы членов геометрической прогрессии в математике вычисляется по формуле
) = q. Суммы членов геометрической прогрессии в математике вычисляется по формуле
 S
S 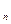 = a
= a 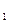 (q
(q  -1) / (q-1), тогда (1) примет вид
-1) / (q-1), тогда (1) примет вид
S = Р ((1+i  )
)  -1)/i
-1)/i  .
.
Коэффициент наращения равен
 k
k 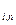 = ((1+i
= ((1+i  )
)  -1)/ i
-1)/ i  .
.
Вычислим теперь современную величину А данного аннуитета. Современное значение каждого платежа будет определяться по формуле
 А
А 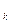 = Р / (1+i
= Р / (1+i  )
) 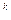 .
.
Тогда современная величина всего аннуитета составит
 А =
А =  ,
,
где а 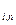 - коэффициент приведения аннуитета. Это опять сумма геометрической прогрессии, теперь уже с параметрами а
- коэффициент приведения аннуитета. Это опять сумма геометрической прогрессии, теперь уже с параметрами а 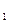 = q = 1/(1+i
= q = 1/(1+i  ). Тогда для а
). Тогда для а 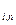 получим
получим

а 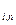 = (1/(1+i
= (1/(1+i  )
)  ((1/1+i
((1/1+i  ) -1)) / (1/(1+i
) -1)) / (1/(1+i  )-1) = (1 - (1+i
)-1) = (1 - (1+i  )
) 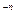 ) / i
) / i  ,
,
для современной величины А соответственно
 А = Р
А = Р  (1 - (1+i
(1 - (1+i  )
) 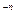 ) / i
) / i  .
.
Видно, что современная величина аннуитета и наращенная сумма связаны соотношением:
 S = А(1+i
S = А(1+i  )
)  .
.
Из полученных формул можно получить выражение для размера очередного платежа:
 Р=S/ k
Р=S/ k 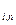 = S
= S  i
i  / (1+i
/ (1+i  )
)  -1 или
-1 или
Р=А/ а 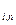 = А
= А  i
i  / (1 - (1+i
/ (1 - (1+i  )
) 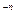 )
)
Рассмотрим теперь аннуитет пренумерандо с теми же условиями.
Отличие от предыдущего случая здесь состоит в том, что период начисления процентов на каждый платеж увеличивается на один год, т.е. каждая наращенная сумма S 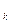 увеличивается в (1+i) раз. Следовательно, для всей суммы имеем
увеличивается в (1+i) раз. Следовательно, для всей суммы имеем
 Sп = (1+i
Sп = (1+i  )
) 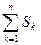 = S(1+i
= S(1+i  ).
).
 Для коэффициента наращения пренумерандо k
Для коэффициента наращения пренумерандо k 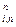 имеем:
имеем:
k 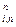 = k
= k 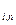 (1+i
(1+i  )
)
Для определения современных значений каждого платежа дисконтирование по заданной ставке i проводится на один раз меньше, чем в случае аннуитета пренумерандо. Поэтому каждая современная величина А 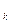 будет больше в (1+i) раз. Таким образом,
будет больше в (1+i) раз. Таким образом,
 Ап=
Ап= 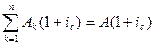 .
.
Для коэффициента приведения получаем
 а
а 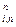 = а
= а 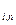 (1+i
(1+i  ).
).
Если срок аннуитета неограничен, мы имеем случай вечного аннуитета - перпетуитета. Для аннуитета пренумерандо выражения для наращенной суммы и современной величины приобретут вид
 S
S 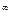 =
= 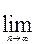 Р
Р  ((1+i
((1+i  )
)  -1)/i
-1)/i  =
= 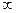 ,
,
А 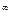 =
= 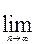 Р
Р  (1-(1+i
(1-(1+i  )
) 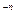 )/i
)/i  = Р: i
= Р: i  .
.
Для аннуитета пренумерандо соответственно получим

Sп 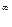 =
= 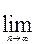 Р
Р  (1+i
(1+i  )
)  ((1+i
((1+i  )
)  -1)/i
-1)/i  =
= 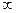 ,
,
Ап 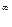 =
= 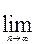 Р
Р  (1+i
(1+i  )
)  (1-(1+i
(1-(1+i  )
) 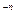 )/i
)/i  = Р + Р / i
= Р + Р / i 
3.2. Концепция учета инфляционного обесценения денег
в принятии финансовых решений.
Концепция учета фактора инфляции в управлении различными аспектами финансовой деятельности предприятия заключается в необходимости реального отражения стоимости его активов и денежных потоков, а также в обеспечении возмещения потерь доходов, вызываемых инфляционными процессами, при осуществлении финансовой деятельности.
Рассмотрим механизм влияния инфляции на результат финансовых операций. Пусть S 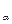 - сумма, покупательная способность которой равна покупательной способности суммы S при отсутствии инфляции. S
- сумма, покупательная способность которой равна покупательной способности суммы S при отсутствии инфляции. S 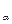 - S =
- S = 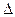 S.
S.
(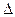 S / S)
S / S)  100% - это выражение называется уровень инфляции.
100% - это выражение называется уровень инфляции.
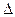 S / S =
S / S = 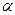 - это темп инфляции.
- это темп инфляции.
Тогда S 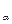 = S +
= S + 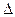 S = S + S
S = S + S 
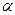 = S(1 +
= S(1 + 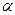 ).
).
(1 + 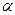 ) = I
) = I 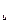 - индекс инфляции. Он показывает, во сколько раз выросли цены.
- индекс инфляции. Он показывает, во сколько раз выросли цены.
Если 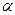 - годовой уровень инфляции, то через год S
- годовой уровень инфляции, то через год S 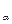 будет больше S в (1 +
будет больше S в (1 + 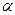 ) раз. Через два года - в (1 +
) раз. Через два года - в (1 + 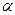 )
) 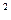 раз, через n лет - в (1 +
раз, через n лет - в (1 + 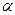 )
)  раз - видна аналогия со сложной процентной ставкой.
раз - видна аналогия со сложной процентной ставкой.
Рассмотрим период в n лет, причем n = n 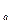 + n
+ n 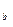 , n
, n 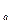 - целое число лет, n
- целое число лет, n 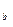 , - оставшаяся дробная часть года. Тогда
, - оставшаяся дробная часть года. Тогда
I 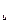 = (1 +
= (1 + 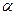 )
) 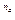 (1 + n
(1 + n 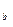

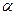 ).
).
Иногда бывает известен уровень инфляции 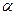
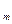 за интервал меньше года, тогда за период, равный m таких интервалов,
за интервал меньше года, тогда за период, равный m таких интервалов,
I 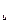 = (1 +
= (1 + 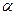
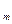 )
) 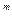 .
.
Пусть 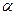 -годовой уровень инфляции, i - простая годовая ставка, тогда S
-годовой уровень инфляции, i - простая годовая ставка, тогда S 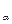 = Р(1 + i
= Р(1 + i 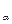 ), в то же время S
), в то же время S 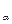 = Р(1 + i)(1 +
= Р(1 + i)(1 + 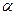 ), следовательно, (1 + i
), следовательно, (1 + i 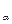 ) = (1 + i)(1 +
) = (1 + i)(1 + 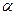 ). Отсюда выведем следующее выражение:
). Отсюда выведем следующее выражение:
i 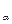 = i +
= i + 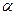 + i
+ i 
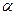
Это выражение называется формулой Фишера, а элемент (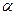 + i
+ i 
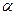 ) - инфляционной премией. Ее нужно прибавлять к процентной ставке для компенсации инфляционных потерь.
) - инфляционной премией. Ее нужно прибавлять к процентной ставке для компенсации инфляционных потерь.
Для простых ссудных процентов S 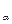 = Р(1 + n
= Р(1 + n  i
i 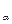 ), в то же время S
), в то же время S 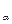 = Р(1 + n
= Р(1 + n  i) I
i) I 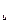 , тогда 1 + n
, тогда 1 + n  i
i 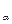 =(1 + n
=(1 + n  i) I
i) I 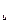 , отсюда i
, отсюда i 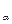 = ((1 + ni) I
= ((1 + ni) I 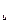 -1) / n.
-1) / n.
Для простых учетных ставок аналогично - 1 / (1 - nd 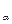 ) = I
) = I 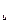 (1 / (1-nd), отсюда d
(1 / (1-nd), отсюда d 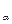 =(I
=(I 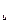 - 1 + nd) / I
- 1 + nd) / I 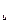 n.
n.
Для сложных ссудных процентов: (1 + i 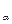 )
)  = (1 + i)
= (1 + i)  I
I 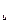 , тогда i
, тогда i 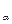 =(1 + i)
=(1 + i) 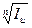 -1; если начисление происходит несколько раз в году, то (1 +
-1; если начисление происходит несколько раз в году, то (1 +  /m)
/m) 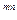 = (1 + j/m)
= (1 + j/m) 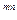 I
I 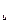 отсюда
отсюда  =m((1 + j/m)
=m((1 + j/m) 
 - 1)
- 1)
Для сложных учетных ставок аналогично: d 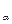 =1- (1-d) /
=1- (1-d) / 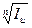 , f
, f 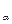 =m(1 - (1-f/m) /
=m(1 - (1-f/m) / 
3.3. Концепция учета фактора риска.
Эффективность любой финансовой или хозяйственной операции и величина сопутствующего ей риска взаимосвязаны. Не учитывая фактора риска невозможно провести полноценный инвестиционный анализ. Таким образом, основная задача -научиться оценивать величину риска и устанавливать взаимосвязь между нею и уровнем доходности конкретной операции.
Концепция учета фактора риска состоит в объективной оценке его уровня с целью обеспечения формирования необходимого уровня доходности финансовых операций и разработки системы мероприятий, минимизирующих его негативные финансовые последствия для деятельности предприятия.
Независимо от происхождения и сущности риска главнейшей цели бизнеса – получению дохода на вложенный капитал – соответствует следующее определение риска.
Риск – это возможность неблагоприятного исхода, т.е. неполучение инвестором ожидаемой прибыли
Чем выше вероятность получения низкого дохода или убытков, тем рискованнее проект. А чем рискованнее проект, тем выше должна быть его норма доходности.
При выборе из нескольких возможных вариантов вложения капитала степень риска можно достаточно точно оценить, а также определить соответствующую данному уровню риску величину доходности проекта.
Дата публикования: 2015-07-22; Прочитано: 1089 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
