 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Сложные ставки ссудных процентов
|
|
Если после очередного интервала начисления доход, т.е. начисленные за данный интервал времени процентов не выплачиваются, а присоединяются к денежной сумме, имеющейся на начало этого интервала, для определения наращенной суммы применяют формулы сложных процентов. Сложные ссудные процентов в настоящее время очень распространены в различных финансовых операциях.
Введем обозначения. Пусть
i  - относительная величина годовой ставки сложных ссудных процентов,
- относительная величина годовой ставки сложных ссудных процентов,
k - коэффициент наращения в случае сложных процентов,
j - номинальная ставка сложных ссудных процентов,
 Если за интервал начисления принимается год, то по прошествии первого года наращенная сумма в соответствии с формулой (1.7) составит
Если за интервал начисления принимается год, то по прошествии первого года наращенная сумма в соответствии с формулой (1.7) составит
S 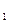 = P (1 + i
= P (1 + i  ),
),
еще через год это выражение применяется уже к сумме S 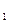
S  = S
= S 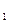 (1+i
(1+i  ) = P
) = P  (1 + i
(1 + i  )
) 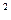
и так далее. По прошествии n лет наращенная сумма составит
S = P  (1 + i
(1 + i  )
) 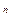 (3.1)
(3.1)
коэффициент наращения соответственно будет равен
k = (1 +i  )
) 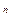 (3.2)
(3.2)
При начислении простых процентов он составил, как мы видели ранее
k = (1 + n  i)
i)
Сравнивая два последних выражения можно видеть, что чем больше период начисления, тем больше разница в величине наращенной суммы при начислении простых и сложных процентов. Поэтому инвестиции на условиях сложного процента более выгоды, чем на условиях простого процента при условии равенства номинальных доходностей в годовом исчислении. Как правило, когда возникает возможность выбора между низкой сложной процентной ставкой и более высокой простой следует отдавать предпочтение первому варианту. Естественно, если в распоряжении есть достаточно длительный период времени. Сумма, наращенная по сложной процентной ставке, уже через небольшое (в зависимости от разницы в величине процентных ставок) количество интервалов начисления превысит сумму, наращенную по простой ставке. Использование в расчетах сложного процента более логично, поскольку в этом случае капитал, генерирующий доходы, постоянно возрастает. Считается что по мере получения любых денежных поступлений, в силу требования рациональности, последние должны наращиваться либо в ходе данного инвестиционного проекта, либо в других инвестиционных проектах.
Применение принципа простого процента, кроме того, стимулирует к изъятию начисленных процентов в пользу текущего потребления, текущей хозяйственной деятельности или другого инвестиционного процесса.
Если срок ссуды n в годах не является целым числом, множитель наращения определяют следующим образом
 k = (1+i
k = (1+i  )
) 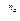
 (1 + n
(1 + n 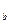
 i
i  ), где
), где
n = n 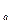 + n
+ n 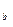 , n
, n 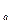 - целое число лет, n
- целое число лет, n 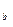 , - оставшаяся дробная часть года.
, - оставшаяся дробная часть года.
Допустим, начисление сложных процентов осуществляется не один, а несколько раз в году. В этом случае оговаривается номинальная ставка процентов j - годовая ставка, по которой определяется величина ставки процентов, применяемая на каждом интервале начисления.
Если в году m равных интервалов, а номинальная ставка процентов j, то на каждом интервале применяется процентов ставка, равная j / m.
Если срок ссуды составляет n лет, то по формуле (3.1), получим выражение для определения наращенной суммы
 S
S 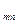 = P(1 + j/m)
= P(1 + j/m) 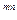 , (3.6)
, (3.6)
где mn - общее число интервалов начисления за весь срок ссуды.
Если общее число интервалов начисления не является целым числом (mn - целое число интервалов начисления, l -часть интервалов начисления), то выражение (3.6) принимает вид
 S = P(1 + j/m)
S = P(1 + j/m) 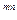
 (1 + l
(1 + l  j /m).
j /m).
В России в настоящее время наиболее распространены начисление процентов по полугодиям, поквартальное и ежемесячное. Такие проценты, начисляемые с определенной периодичностью, называются дискретные.
В мировой практике часто применяется непрерывное начисление сложных процентов, т.е. продолжительность интервала начисления стремится к нулю, а число интервалов m -к бесконечности.
В этом случае для вычисления наращенной суммы служит следующее выражение
 S = P
S = P 
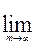 (1 + j/m)
(1 + j/m) 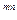 (3,8)
(3,8)
Для расчетов в этом случае можно использовать известную в математике формулу второго замечательного предела:

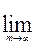 (1 + 1/m)
(1 + 1/m) 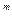 = e, где е = 2,71828....
= e, где е = 2,71828....
из этой формулы следует 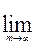 (1 + j/m)
(1 + j/m) 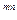 = е
= е 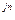 .
.
Тогда для наращенной суммы получаем
 S = P
S = P  e
e 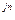 (3.9)
(3.9)
Здесь k = e 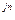 (3.10)
(3.10)
Значение наращенной суммы тогда можно вычислять, находя значения экспоненты в той или иной степени в спец. таблицах.
Очевидно, что непрерывным способ начисления процентов дает максимальную величину наращенной суммы при прочих равных условиях.
Из формулы (3.1) получаем
 P = S: (1+i
P = S: (1+i  )
)  = S
= S  a. (3.11)
a. (3.11)
Если вспомнить, что, как и в случае простых процентов, определение настоящей величины суммы S называется дисконтированием, то коэффициент а назовем коэффициентом дисконтирования. Эта величина обратна коэффициенту наращения, т.е.
 k
k  а = 1.
а = 1.
Формула (3.11) дает понять, что текущий финансовый эквивалент будущей денежной суммы тем ниже, чем отдаленнее срок ее получения и чем выше норма доходности.
Найдем выражения для величин i, j, n.
 Из формулы (3.1) получаем i
Из формулы (3.1) получаем i  =
= 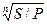 - 1.
- 1.
Из формулы (3.6): j = m(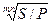 - 1).
- 1).
Преобразуем формулу (3.1): S/P = (1+i  )
)  .
.
Прологарифмируем обе части равенства:
ln S/P = ln (1+i  )
)  = n
= n  ln (1 + i
ln (1 + i  ).
).
Тогда n = (ln S/P) / ln(1 + i  ).
).
Аналогично из формулы (3.6) получим
n = (ln S/P) / m ln(1 + i  ).
).
Дата публикования: 2015-07-22; Прочитано: 286 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
