Интегралы от функций с особыми точками

Точка х₀ называется особой для функции f(x), если 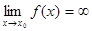, т.е. если функция f(x) является бесконечно большой в точке х₀.

По определению:

если функция f(x) определена на полуинтервале [a, b) и b – ее особая точка, то

;

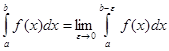если функция f(x) определена на полуинтервале (a, b] и a – ее особая точка, то

;

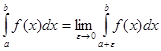если функция f(x) определена на отрезке [a, b] за исключением ее внутренней особой точки с, то

,

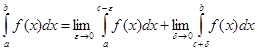причем величины e и d стремятся к нулю независимо друг от друга.

Если указанные пределы существуют, то соответствующие несобственные интегралы сходятся; если не существуют – расходятся. Если в последнем случае существует предел

,

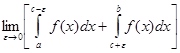то он называется главным значением несобственного интеграла.

Очевидны обобщения определений несобственного интеграла для нескольких особых точек на отрезке [a, b]; мы не будем на этом останавливаться.

Пример 2.9.

Рассмотрим несобственный интеграл с особой точкой b, .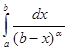

Если a ¹ 1, то 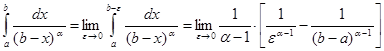. Этот предел существует, если a < 1; при a > 1 предел не существует. Если же a = 1, то 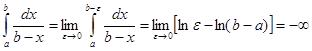. Таким образом, несобственный интеграл 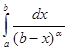сходится при a < 1 и расходится при a ³ 1. К аналогичным выводам мы придем относительно несобственного интеграла 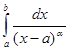с особой точкой a. n

Достаточные признаки сходимости интегралов от функций с особыми точками. Как и в случае интегралов с бесконечными пределами, нам будет достаточно ограничиться рассмотрением только одного случая – случая, когда особая точка совпадает с правым концом отрезка интегрирования [a, b].

Критерий Коши. Несобственный интеграл 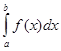, где b – особая точка функции f(x), сходится тогда и только тогда, когда для любого e > 0 существует число h Î [a, b), такое что для любых h', h" из интервала (h, b) выполняется неравенство

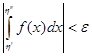.n

Если существует интеграл 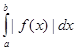, то существует и интеграл 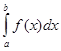, где b – особая точка функции f(x); в этом случае несобственный интеграл 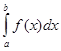называется абсолютно сходящимся.

Признак сравнения. Если для функции f(x) ³ 0 на [a, b), имеющей особую точку b, существует предел

,

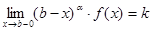то при a < 1 и 0 £ k < +¥ несобственный интеграл 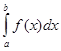сходится, а при a ³ 1 и 0 < k £ +¥ несобственный интеграл расходится.n

Пример 2.10.

Рассмотрим несобственный интеграл 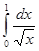; здесь особая точка x = 0. Возьмем в качестве функции сравнения x^2/3,т.е. a = 2/3. Тогда x^2/3 × f(x) = x^2/3 × x^-1/2 = x^1/6® 0 при х ® 0, т.е. k = 0. Следовательно, интеграл сходится.

Напротив, для несобственного интеграла 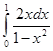с особой точкой x = 1 признак сравнения дает отрицательный результат. Действительно, в этом случае пробную функцию следует взять в виде 1 – x, т.е. a = 1; при меньших a выражение 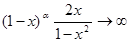при х ®1. При a = 1 имеем 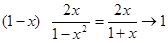при х ®1, т.е. k = 1n

Предостережение. При вычислении несобственных интегралов 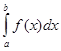с особыми точками внутри промежутка интегрирования нельзя механически применять формулу Ньютона – Лейбница, поскольку это может привести к ошибкам.

Общее правило: формула Ньютона – Лейбница верна, если первообразная от f(x) в особой точке последней непрерывна.

Пример 2.11.

Рассмотрим несобственный интеграл 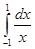с особой точкой х = 0. Формула Ньютона–Лейбница, применяемая формально, дает

.

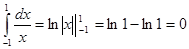Однако общее правило здесь не выполняется; для f(x) = 1/x первообразная ln |x| не определена в х = 0 и является бесконечно большой в этой точке, т.е. не является непрерывной в этой точке. Непосредственной проверкой легко убедиться, что интеграл 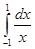расходится. Действительно,

.

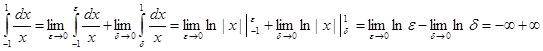Полученная неопределенность может быть раскрыта по-разному, поскольку e и d стремятся к нулю независимым образом. В частности, полагая e = d, получаем главное значение несобственного интеграла, равное 0. Если e = 1/n, а d =1/n², т.е. d стремится к 0 быстрее, чем e, то получаем

;

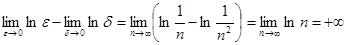пр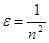и и 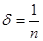, наоборот,

,

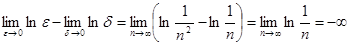т.е. интеграл расходится.n

Пример 2.12.

Рассмотрим несобственный интеграл 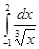с особой точкой х = 0. Первообразная от функции 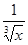имеет вид 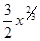и непрерывна в точке х = 0. Поэтому можно применить формулу Ньютона – Лейбница:

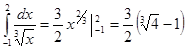n