Экстремум функции одной переменной

Говорят, что точка х₀ является точкой строгого локального максимума (минимума) заданной функции f(x), если существует такая d - окрестность точки х_0, что для любой точки х из этой d - окрестности, х ¹ х_0, выполняется условие f(x) < f(x₀) (f(x) > f(x₀)). При замене знака < на £ получается определение для нестрогого локального максимума (минимума).

В этом разделе для краткости будем писать просто «максимум (минимум) функции», имея в виду локальный максимум (локальный минимум) функции.

Максимум или минимум функции называют собирательным термином экстремум функции.

Пример 1.8.

1) Функция имеет в точке х₀ = 0 строгий локальный максимум, но локальных минимумов она не имеет.

2) Функция f(x) = sin x имеет в точках , k = 0, ±1, ±2,¼,строгие локальные максимумы равные 1, а в точках , k = 0,, ±1, ±2,¼ - строгие локальные минимумы, равные –1.n

Теорема Ферма (необходимое условие экстремума (строгого и нестрогого) дифференцируемой функции). Если действительная функция f(x) определена в окрестности точки х_0, дифференцируема в этой точке и имеет в ней экстремум, то ее первая производная в точке х₀ равна 0: f'(x₀) = 0n

Достаточное условие строгого экстремума дифференцируемой функции. Если действительная функция f(x) определена в окрестности точки х₀, дважды дифференцируема в этой точке и имеет в ней нулевую первую производную f^'(x₀) = 0, а также отрицательную (положительную) вторую производную f"(x₀) < 0 (f"(x₀) > 0), то функция f(x) достигает в х₀ своего строгого максимума (минимума)n

Для геометрической интерпретации условий существования экстремума дифференцируемой функции полезным оказывается понятие выпуклости графика этой функции и его связь со знаком второй производной.

График функции f(x) называется выпуклым вверх (вниз) на интервале (a, b), если он целиком расположен не выше (не ниже) любой касательной к нему на интервале (a,b). Если, кроме того, график имеет не более одной общей точки с любой касательной к нему на интервале (a,b), то он называется строго выпуклым.

Если график дважды дифференцируемой функции f(x) строго выпуклый вверх (вниз) на интервале (a,b), то f"(x) < 0 (f"(x) > 0) на этом интервале; верно и обратноеn

Теперь проиллюстрируем условия существования строгих экстремумов.

Пусть действительная функция f(х) имеет в точке х₀ строгий локальный максимум, дважды дифференцируема в некоторой окрестности точки х₀ и имеет строго выпуклый вверх график (см. рис. 1.6). Поскольку f (x₀) является наибольшим значением функции в этой окрестности, то по теореме Ферма в точке х₀ f'(x₀) = 0 и касательная в ней горизонтальна. В силу строгой выпуклости графика первая производная в точках х_1, х₂ должна быть положительна, а в точках х₃ и х₄ должна быть отрицательна. Более того, первая производная должна монотонно убывать в этой окрестности, т.е. , поскольку 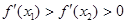, а . Именно поэтому вторая производная функции f(х), которая имеет смысл скорости изменения первой производной, должна быть в этой окрестности отрицательной, т.е. 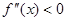. В частности, f"(x₀)< 0.

Иллюстрация для случая строгого локального минимума представлена на рис. 1.7. Рассуждения, аналогичные предыдущему случаю, приводят нас к выводу, что первая производная должна строго возрастать, т.е. tg a₁ < tga₂ < 0, а 0 < tgb₁ < tgb₂, принимая нулевое значение в точке х₀, f'(x₀) = 0.

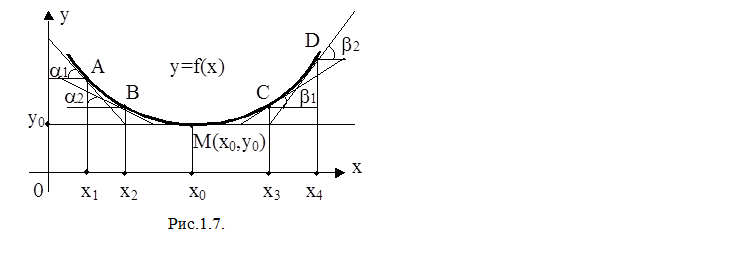Поэтому вторая производная функции f должна быть в окрестности точки х₀ положительной, . В частности, f"(x₀) > 0.

На рис. 1.8 изображен случай, когда функция f(x) имеет в точке х₀ нулевую производную (геометрически это означает, что касательная к графику в точке М (х₀ ,y₀) горизонтальна), но точка х₀ не является точкой экстремума, поскольку в этой точке (действительно, левее х₀ 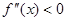, а правее х₀ , чему геометрически соответствует разное направление строгой выпуклости графика). Данное обстоятельство иллюстрирует важность понятия так называемых точек перегиба.

Пусть функция f определена в некоторой окрестности точки х₀ и дважды дифференцируема в этой окрестности. Точка х₀ называется точкой перегиба функции f, если она одновременно является концом интервала строгой выпуклости вверх ) и концом интервала строгой выпуклости вниз (.

На рис.1.8 график функции «перегибается» через касательную к нему в точке М (х₀, y₀=f(x₀)). На рис. 1.9 при х < x₁ график функции f₁(x) лежит под касательной, а при х > х₁ – над ней; наоборот, при х < x₂ график функции f₂(x) лежит над касательной, а при х >x₂ – под ней.

Необходимое условие существования точки перегиба – равенство 0 второй производной в этой точке, т.е. . Достаточное условие точки перегиба: и n

1.6. ИССЛЕДОВАНИЕ ФУНКЦИЙ
И ПОСТРОЕНИЕ ИХ ГРАФИКОВ

Изложим схему исследования.

1. Найти область определения функции; определить, четная она или нечетная. Если f(x) = f(-x), т.е. функция четная, то достаточно исследовать ее для полуоси х ³ 0, а для х £ 0 зеркально отобразить ее график относительно оси ординат, как показано на рис.1.10.

Если f(x) = - f(-x), т.е. функция нечетная, то она исследуется для х ³ 0, азатем для х £ 0 ее график отображается дважды: сначала относительно оси ординат, а затем – в левой полуплоскости относительно оси абсцисс, как показано на рис.1.11.

2. Найти точки пересечения графика функции с осями координат. Дело сводится к решению уравнения y = f(x) = 0 и нахождению его корней, а также к вычислению значения y₀ = f(0).

3. Найти асимптоты функции. Асимптоты бывают вертикальными, горизонтальными и наклонными.

Вертикальные асимптоты: прямые вида х =х₀, где х₀ определяются из условия ;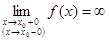

Горизонтальные асимптоты: прямые вида y = y₀, где y₀ определяется из условия ;

Наклонные асимптоты имеют вид: y = kx + b (k ¹ 0), где = , .

На рис. 1.12. вертикальная асимптота имеет вид х = 0 (ось ординат); горизонтальная асимптота имеет вид y = 1 при х ® - ¥; наклонная асимптота имеет вид луча ОМ, для которого b = 0, при х ® + ¥. Функция f не является ни четной, ни нечетной.

4. Найти точки локальных экстремумов функции. Для этого требуется решить уравнение f'(x) = 0 и убедиться, что для его корней вторая производная отлична от 0, т.е. , если .

5. Найти точки перегиба функции. Это точки, в которых вторая производная обращается в 0, т.е. .

6. Исследовать знаки первой и второй производных. Определить участки возрастания и убывания функции, найти направление выпуклости графика, точки экстремумов, точки перегиба. Построить вспомогательный график.

Функция убывает (возрастает) на некотором интервале, если ее первая производная отрицательна, f'(x) < 0 (положительна, f'(x) > 0). График функции выпуклый вверх на некотором интервале, если f''(x) < 0, т.е. вторая производная отрицательна (соответственно, вниз, если f''(x) > 0). Точки локальных экстремумов определяются из условия f'(x₀) = 0, f''(x₀) ¹ 0. Знак второй производной определяет характер экстремума (максимум или минимум). Точка перегиба определяется условием f''(x₀) = 0, f'''(x₀) ¹ 0. При построении вспомогательного рисунка надо следить за согласованностью результатов исследования функции.

7. Построить график функции, учитывая результаты исследования. Здесь учитываются все результаты, в том числе четный или нечетный характер функции. График строится с той степенью точности, которая характеризует качественное поведение функции. Точно указываются лишь параметры асимптот, точки пересечения с осями координат, точки локальных экстремумов и их значения, точки перегиба. Возрастание или убывание функции, направление выпуклости отображается приближенно, с точным указанием лишь границ интервалов, на которых функция возрастает или убывает, выпукла вверх или вниз.

Пример 1.9.

Исследовать функцию и построить ее график.

1. Область определения функции совпадает с действительной отрицательной полуосью, т.е. {x: x £ 0}. Функция не является ни четной, ни нечетной.

2. Точка (0, 0) очевидна; решаем уравнение х²- 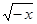= 0. Оно имеет единственный действительный корень, отличный от 0, он равен – 1; следовательно, график пересекает ось абсцисс также в точке – 1.

3. Ни для одного х₀, х₀ £ 0, функция не имеет бесконечного предела, т.е. вертикальных асимптот нет. Поскольку , то нет и горизонтальных асимптот. Отсутствует также и наклонная асимптота, поскольку .

4. Вычисляем первую и вторую производные.

; ;

Уравнение y' (x) = 0 имеет единственное действительное решение х = ; при этом , что соответствует локальному минимуму. Его значение равно .

5. Критических точек, соответствующих решению уравнения y'' (x) = 0, нет.

6. Первая производная в интервале (-¥, ) отрицательна, в интервале (, 0) – положительна. Следовательно, функция в интервале (-¥, ) убывает, в точке достигает своего локального минимума , затем в интервале (, 0) растет, достигая значения y(0) =0 с производной (односторонней) y'(0) = +¥, т.е. график входит в точку 0 вертикально. При этом график на всей области определения выпуклый вниз, причем строго, поскольку вторая производная на всем интервале (-¥,0) положительна.

7. С учетом вышеизложенного вид графика приведен на рис. 1.13.n

1.7. ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Пусть X,Y и Z – некоторые числовые множества, являющиеся подмножествами действительных чисел из R. Действительной функцией двух переменных называется функция f: X ´ Y ® Z, ставящая в соответствие каждой упорядоченной паре (x, y) из множества X ´ Y единственное число f(x, y) Î Z. Число z = f(x, y) называют значением функции f в точке (x, y). Переменную z называют зависимой переменной, а переменные x и y – независимыми переменными (или аргументами). Множество X ´ Y называется областью определения функции f, а множество {z: $ (x, y) Î X ´ Y, z = f(x, y)} Í Z называется областью значений функции f.

Понятие действительной функции нескольких переменных является естественным обобщением понятия действительной функции одной переменной. Мы ограничимся случаем двух переменных, поскольку расширение рассмотрения на случай произвольного конечного числа переменных вполне очевидно и связано, как правило, с излишней громоздкостью изложения.

Пусть задана числовая последовательность точек из множества X ´ Y, т.е. последовательность упорядоченных пар чисел {(x_n, y_n)}, n = 1, 2, …

Говорят, что последовательность точек {(x_n, y_n)}, n = 1, 2, … сходится к точке (A, B) Î X ´ Y, если для любого e > 0 существует натуральное число N такое, что для всех n > N выполняется неравенство .

Сходящуюся последовательность точек обозначают как или . Из сходимости последовательности точек следует сходимость компонентных последовательностей, т.е. 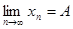, и наоборот.

Понятия предела и непрерывности для действительной функции одной переменной также естественно обобщаются на случай действительной функции нескольких переменных.

Число А называется пределом функции f(x, y) = z в точке (x₀, y₀), если для любой сходящейся к (x₀, у₀) последовательности точек {(x_n, y_n)}, n = 1, 2, …, , соответствующая последовательность значений функции {f(x_n, y_n)}, n = 1, 2, … сходится к А, что обозначается как .

Читателю предлагается самостоятельно сформулировать эквивалентное понятие предела функции двух переменных на языке окрестностей, в духе критерия Коши.

Действительная функция двух переменных f: X ´ Y ® Z непрерывна в точке (x₀, y₀) Î X ´ Y, если для любой сходящейся к (x₀, y₀) последовательности точек {(x_n, y_n)}, n = 1, 2, …, 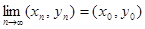, соответствующая последовательность значений функции {f(x_n, y_n)}, n = 1, 2, … сходится к значению функции в точке (х₀, y₀), т.е. .

Это определение непрерывности функции двух переменных в точке также предлагается читателю перевести в эквивалентную форму на языке окрестностей.

Обратим внимание на следующее обстоятельство, не имеющее аналога в случае функции одной переменной. Функция f двух переменных, непрерывная в точке (x₀, y₀), называется также непрерывной в этой точке по совокупности переменных x, y; наряду с этой непрерывностью используют понятие непрерывности по отдельным переменным.

Зафиксируем значение второго аргумента y₀ и будем рассматривать точки вида (x, y₀), х Î Х. Ясно, что при этом функция двух переменных f(x, y) = z превращается, по существу, в функцию f(x, y₀) одной переменной х_.

Функция двух переменных f(x, y) = z называется непрерывной в точке (x₀, y₀) по переменной х, если в точке х₀ непрерывна функция f(x, y₀), рассматриваемая как функция одной переменной х. Аналогично определяется непрерывность в точке (x₀, y₀) по переменной y.

Оказывается, что функция f: X ´ Y ® Z может быть непрерывной в точке (x₀, y₀) по каждой переменной x, y в отдельности, но одновременно не быть непрерывной в этой точке по совокупности переменных.

Пример 1.10.

Рассмотрим функцию двух переменных 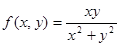, доопределив ее в точке (0, 0) нулевым значением, т.е.f(0,0)=0. Ясно, что f(x,y) определена в любой точке множества R ´ R. Исследуем ее непрерывность в точке (0, 0).

Обе функции одной переменной f (x, 0) и f (0, y), определенные на соответствующих координатных осях (f(x, 0) – на оси абсцисс, f(0, y) – на оси ординат), тождественно равны на них нулю. Поэтому функция f(x,y) непрерывна в точке (0, 0) по каждой своей переменной x и y.

Однако она не является непрерывной в точке (0. 0) по совокупности переменных. Действительно, будем приближаться к точке (0,0) – началу координат- по лучу y = kx, k ¹ 0. Вдоль этого луча значение функции равно , т.е. n