Методы, предполагающие линеаризацию целевой функции

В основе методов оценки параметров эконометрической модели, предполагающих линеаризацию целевой функции, т. е. суммы квадратов ошибки модели S ²(a, х) по переменным a ₀, a ₁,..., a_п, лежат свойства ее градиента Ñ S ², согласно которым направление этого вектора в произвольной многомерной точке пространства параметров a ₀ ^j, a ₁ ^j,..., a_п^j указывает направление наибольшего роста функции S ²(a, х) в этой точке. Соответственно противоположный вектор указывает на направление наибольшего уменьшения (наискорейшего спуска).

Здесь следует подчеркнуть, что направление наискорейшего спуска в некоторой точке пространства параметров не обязательно указывает на точку оптимума функции S ². Однако двигаясь в этом направлении, можно попасть в следующую точку, в которой направление движения уточняется. А результате последовательность точек должны привести к искомому решению.

Градиент целевой функции S ²(a, х) в произвольно выбранной исходной (нулевой) точке пространства параметров a ₀⁰, a ₁⁰,..., a_п ⁰ может быть определен на основе ее разложения в ряд Тейлора первого порядка:

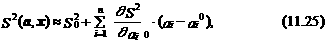
где S ₀²= S ²(a ⁰, х) – значение суммы квадратов ошибки модели в точке пространства ее параметров a ⁰; – первая производная функции S ²(a, х) по параметру a_i в точке a ⁰; a_i – a_i ⁰ – прирост i -го параметра.

Координаты вектора –Ñ S ²(a ⁰, х), сформированного на основании составляющих правой части выражения (11.25) как

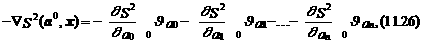
определяют направление наискорейшего спуска (направление оптимального движения к точке минимума S ²(a, х) по оценкам параметров эконометрической модели).

Прямое использование выражения (11.26) при определении “оптимальных” оценок a ₀, a ₁,..., a_п, минимизирующих сумму квадратов ошибок модели, лежит в основе метода наискорейшего спуска. Согласно этому методу оптимальные оценки находятся на основе итеративной процедуры расчетов последовательности таких оценок a ⁰, a ¹,..., a ^j, в которой каждая следующая оценка лежит на направлении наискорейшего спуска, определенного в предыдущей точке.

Направление движения, например, из начальной точки a ⁰ указывает единичный вектор, определяемый следующим выражением:

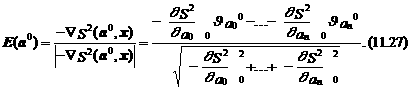
Например, если для модели с двумя параметрами a ₀ и a ₁ градиент функции S ²(a ₀⁰, a ₁⁰) равен

Ñ S ²(a ⁰)=3 Ja ₀⁰–2 Ja ₁⁰,

то соответствующий единичный вектор определяется как

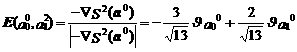
и соответственно пропорции приростов значений параметров D a ₀⁽¹⁾ и D a ₁⁽¹⁾ должны быть равны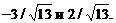

На практике оценку a _i ^(j), i =0,1,..., п согласно методу наискорейшего спуска определяют с помощью выражения, аналогичного (11.19)

a_i ^(j)= a_i ^{(j –1)}+ h_i ^(j)×D a_i ^(j), (11.28)

где h_i ^(j) – множитель, оптимизирующий размер прироста параметра j -м шаге расчетов.

Некоторые недостатки метода наискорейшего спуска обусловлены зависимостью направления движения от формы поверхности S ²(a). Поскольку направление “наискорейшего спуска” в каждой точке пространства параметров a указывает не на место расположения минимума суммы квадратов ошибки, а лишь на направление ее наибольшего убывания в этой точке, то в случае “неправильных” (существенно отличающихся от “шарообразных”) форм поверхности S ²(a) метод наискорейшего спуска “выбирает” достаточно продолжительный маршрут движения к оптимуму.

Для ускорения этого движения Макуардт предложил комбинированный (компромиссный) метод оценки параметров эконометрической модели, объединяющий идеи методов Гаусса-Зайделя и наискорейшего спуска. В его основе лежат два следующих замечания. Во-первых, вектор приростов параметров на j -м шаге расчетов по методу наискорейшего спуска можно представить в следующем виде:

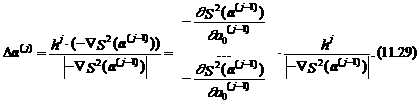
Во-вторых, заметим, что производные функции S ²(a ^{(j –1)}) по своим аргументам a ₀ ^{j– 1}, a ₁ ^{j– 1},..., a_п^{j– 1} равны компонентам вектора (Х _{j– 1}¢· g ^{j– 1}) из правой части выражения (11.22):

где z_i ^{(j– 1)} – i -я компонента вектора Х _{j– 1}¢× g ^{j– 1}, полученная на j -м шаге расчетов.

С учетом (11.29) вектор приростов параметров на j -м шаге расчетов находится как

где 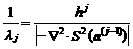– константа.

Сопоставим выражения (11.22) и (11.31). Получим

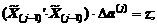
Макуардт объединил оба выражения из (11.32) в одно:

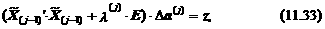
где Е – единичная матрица, и предложил выбирать множитель l ^(j), регулирующий длину прироста параметров j -м шаге расчетов, исходя из свойств функции S ²(a ^{(j –1)}). Логика такого выбора определяется следующими соображениями. Если матрица 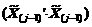плохо обусловлена, где, напомним, матрица 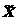в данном случае определена выражением (11.20), то l ^(j) должно быть выбрано достаточно большим и в этом случае приросты параметров в большей степени соответствуют их оценкам, полученным по методу наискорейшего спуска. При хорошей обусловленности матрицы 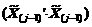, свидетельствующей о быстрой сходимости метода Гаусса-Зайделя, значение l ^(j) выбирается относительно небольшим. Промежуточные значения l ^(j) характеризуют направление движения к минимуму, полученное как комбинация направлений, определенных с помощью методов Гаусса-Зайделя и наискорейшего спуска.

В окрестности минимума метод Макуардта, как и другие методы, уменьшает длину прироста параметров.

Заметим, что методы, основанные на линеаризации суммы квадратов ошибки эконометрической модели, также как и другие итеративные методы поиска оптимальных оценок ее параметров, могут привести к решению, соответствующему локальному оптимуму. Для определения глобального минимума необходимо, как и в случае других методов, решить задачу оценки с использованием разных вариантов исходных точек a ⁰, соответствующих разным участкам допустимой области существования искомых значений параметров.