 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Передаточные функции и характеристики разомкнутых систем
|
|
Системы автоматического управления в большинстве случаев являются замкнутыми. Однако при их анализе и проектировании часто предварительно рассматривается разомкнутая цепь звеньев, которая затем замыкается.
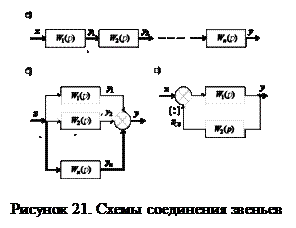
Различают последовательное, параллельное и параллельное с обратной связью соединения звеньев (рис. 21).
1. Последовательным соединением звеньев называют такое соединение, когда выходная величина предыдущего звена, является входной величиной последующего звена (рис.21,а). Если последовательно соединяются звенья m и n, то ym = xn.
Передаточная функция всей цепи:
Передаточные функции звеньев:
где: Y (p), Y (p), …, Yn (p)- изображение по Лапласу соответствующих переменных.
Если перемножить правые и левые части полученных равенств получим:
Поскольку все промежуточные переменные Y 1(p), Y2 (p),…, Yn-1 (p), при перемножении сократятся, то:
Передаточная функция разомкнутой цепи последовательно соединенных звеньев равна произведению передаточных функций всех звеньев.
Переходя от передаточных функций к частотным характеристикам системы, т.е. полагая что p = jω, получим:
- передаточная функция.
Представив 
в виде: 
, находим:
· АЧХ: 
;
· ФЧХ: 
;
· асимптотическая ЛАЧХ: 
Таким образом, при последовательном соединении звеньев амплитудно-частотные характеристики перемножаются, логарифмически амплитудно-частотные и фазовые частотные характеристики складываются.
Рассмотрим получение частотных характеристик разомкнутой цепи при последовательном соединении звеньев. Пусть передаточная функция разомкнутой цепи имеет вид:
.
Причем 0,5 < ξ < 1 (при таком ξ можно не учитывать «горб» АЧХ колебательного звена).
Логарифмическую асимптотическую АЧХ можно построить непосредственно по передаточной функции. ЛАЧХ является ломанной линией. При этом согласно характеристикам типовых звеньев каждому сомножителю (Tp+ 1) в знаменателе соответствует точка излома характеристики при w =1/T с последующим наклоном минус 20 дБ/декаду, а каждому сомножителю такого же типа в числителе соответствует точка излома также при w = 1/T, но с последующим наклоном плюс 20 дБ/декаду. Сомножителю типа T2p2+2ξTp+ 1 в знаменателе соответствует излом характеристики при w =1/T с наклоном минус 40 дБ/декаду.
2. Параллельным соединением звеньев называется такое соединение, когда на входе всех звеньев подается одна и та же величина, а выходные сигналы суммируются (рис. 21,б). Если параллельно соединяются n звеньев, то входной сигнал x = x1 = …= xi = …= xn, а выходной сигнал:
.
Переходя к изображению и учитывая, что Y (p) = Wi (p)∙ Xi (p), получим:
, т.е. 
- передаточная ф-я.
Следовательно:
переходная функция: 
, весовая функция: 
.
Таким образом, при параллельном соединении звеньев передаточные, переходные и весовые функции каждого звена суммируются.
3. При параллельном соединении звеньев с обратной связью обратная связь может быть положительной, если сигнал обратной связи хос складывается с входным сигналом х, или отрицательной, если сигнал обратной связи хос вычитается из х (рис. 21,в).
При наличии отрицательной обратной связи (ОС) схема описывается следующим уравнением:
.
В свою очередь Xос (p) определяется в соответствии с выражением:
.
Подставив значение Xос (p) в выражение для Y (p), получим:
.
Решим это уравнение относительно Y (p):
.
Отсюда:
.
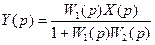Передаточная характеристика системы при наличии положительной/отрицательной обратной связи:
.
Методика построения ЛАЧХ сводится к следующему (рис. 22):
1) определение сопрягающих частот типовых звеньев в порядке возрастания:
; 
; 
; 
; 
;
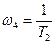2) вычисление на частоте w = 1 ординаты L (1) = 20∙lg k, где k - общий коэффициент передачи разомкнутой системы. Через полученную точку проводят низкочастотную асимптоту ЛАЧХ, представляющую собой при w < 1 прямую с наклоном минус (20∙ r) дБ/декаду, где r - число интегрирующих звеньев;
3) изменение наклона ЛАЧХ на сопрягающих частотах по сравнению с тем наклоном, который она имела до рассматриваемой частоты.
Фазовая частотная характеристика (ФЧХ) строится в соответствии с уравнением (рис. 22):
3. УСТОЙЧИВОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
3.1. Понятие устойчивости линеаризованных систем
Устойчивость – это свойство системы возвращаться в исходное состояние после выхода ее из этого состояния и прекращения действия возмущения. Состояние системы может быть устойчивым и нейтральным. Классическим примером этого утверждения является поведение шарика на различных поверхностях (рис. 23): а -устойчивое, безразличное на горизонтальной плоскости, при котором шар может занимать произвольное положение на плоскости; такое равновесие называют нейтрально устойчивым; б -устойчивое в низшей точке впадины криволинейной поверхности, при котором состояние равновесия единственно; в - неустойчивое на вершине «холма»; положение б устойчиво внутри области MN и неустойчиво на ее границе N.
Исходное состояние системы, устойчивость которой необходимо оценить, необязательно является состоянием покоя. Так, например, можно оценить устойчивость движения спутника, как его способность возвращаться на исходную орбиту после прекращения действия сил, отклоняющих спутник от заданной орбиты.
Впервые наиболее существенные математические результаты по устойчивости движения механических систем получил русский ученый А.М. Ляпунов в 1880÷1910 годах, который доказал, что для устойчивости системы необходимым и достаточным условием является отрицательность вещественных частей всех корней характеристического уравнения, т.е. все корни должны располагаться в левой полуплоскости комплексного переменного р.
Рассмотренное условие устойчивости относится к линейным САУ. Но практически все реальные САУ являются нелинейными и только приближенно многие из них можно описывать линейными уравнениями. Ляпунов сформулировал теоремы, позволяющие по устойчивости линеаризованной системы судить об устойчивости исходной нелинейной системы:
1) если линеаризованная система устойчива, то устойчива и исходная нелинейная система;
2) если линеаризованная система неустойчива, то неустойчива и исходная нелинейная система.
3.2. Алгебраические критерии устойчивости
Ранее было сформулировано условие устойчивости линейных систем в виде требований к корням характеристического уравнения. Однако вычисление корней уравнения высокой степени трудно. Поэтому были введены критерии устойчивости, позволяющие судить об устойчивости или неустойчивости системы по коэффициентам характеристического уравнения без вычисления его корней.
Первый алгебраический критерий устойчивости, который применим для систем третьего порядка, сформулировал русский ученый Н.А. Вышнеградский в 1876 г.: для устойчивости линейной системы с характеристическим уравнением a0p3+a1p2+a2p+ a3 необходимо выполнение двух условий:
1) все коэффициенты характеристического уравнения должны быть положительными;
2) произведение средних коэффициентов должно быть больше произведения крайних, т.е.:
a1a2 > a0a3.
Для определения устойчивости систем любого порядка применяют критерий Гурвица и критерий Рауса.
По критерию Гурвица система будет устойчива, если определитель Гурвица, все его диагональные миноры и первый коэффициент характеристического уравнения а0 положительны т.е.: 
.
Определитель Гурвица строится по коэффициентам характеристического уравнения:
По главной диагонали определителя слева на право выписываются все коэффициенты характеристического уравнения от а1 до аn, в порядке возрастания индексов. Столбцы вверх от главной диагонали дополняют коэффициентами характеристического уравнения с последовательно возрастающими индексами. А столбцы вниз - коэффициентами с последовательно убывающими индексами. Максимальный индекс коэффициента n (n - порядок характеристического уравнения), минимальный - нуль. Столбец заполняется до положенного числа n элементов нулями.
Отмечая в определителе Гурвица диагональные миноры, получим определители низшего порядка
.
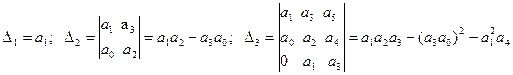Номер диагонального минора определяется номером коэффициента по диагонали, для которого составляется минор.
Исследуя с помощью критерия Гурвица устойчивость систем первого, второго, третьего и более высоких порядков, можно сделать вывод: для системы n -го порядка необходимым условием устойчивости является положительность всех коэффициентов.
По критерию Рауса система устойчива, если коэффициент а0 старшего члена уравнения больше нуля и все элементы первого столбца таблицы Рауса отличны от нуля и положительны.
| № строки | № столбца | |||
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| 
| 
| 
| |
| … | … | … | … |
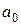
Таблица Рауса составляется по следующим правилам: первая строка составляется из четных коэффициентов уравнения (a0, a2 и т.д.), а вторая - из нечетных (a1, a3 и т.д.), в третью и последующие строки записывается разность произведений коэффициентов, деленная не нечетный коэффициент предыдущей строки, находящийся в первом столбце.
Составление таблицы прерывается, как только первый элемент какой-либо строки оказывается отрицательным или равным нулю.
3.3. Частотные критерии устойчивости
3.3.1. Критерий устойчивости Михайлова
Этот критерий устойчивости, сформулированный в 1938 г. русским ученым А.В. Михайловым, позволяет судить об устойчивости системы на основании рассмотрения векторной кривой, называемой кривой (годографом) Михайлова.
Пусть дано характеристическое уравнение системы:
.
Если подставить в это выражение p = jω, то получится уравнение комплексного вектора:
.
Конец этого вектора при изменении ω от 0 до ¥ опишет некоторую кривую, называемую кривой (годографом) Михайлова. Кривая Михайлова начинается на вещественной оси при ω = 0 в точке [ Х (0) = аn, jV = 0 ] и заканчивается в n -ом квадранте (при ω = ¥), если отсчет квадрантов вести против часовой стрелки. В n -ом квадранте кривая Михайлова уходит в бесконечность.
Чтобы построить кривую Михайлова, необходимо в выражении D (jω) выделить действительную и мнимую части. Далее задаваясь различными значениями 
необходимо найти точки:
[ X (0), jV (0)]; [ X (ω 1), jV (ω1)]; [ X (ω2), jV (ω2)]; … и т.д.
По этим точкам и строят на комплексной плоскости кривую Михайлова.
Согласно критерию Михайлова линейная система n -го порядка устойчива, если кривая (годограф) Михайлова охватывает начало координат и последовательно проходит n квадрантов.
Если кривая Михайлова проходит через начало координат, то система находится на границе устойчивости.
На рисунке 24 показаны кривые Михайлова для устойчивых систем, описываемых уравнениями, начиная от первого (n = 1) и кончая пятым (n = 5) порядком.
Из рисунка видно, что предпоследняя система находится на границе устойчивости, а последняя – неустойчива.
3.3.2. Критерий устойчивости Найквиста
Критерий, предложенный в 1932 г. американским ученым Г. Найквистом, позволяет судить об устойчивости замкнутой системы по амплитудно-фазовой частотной характеристики (АФЧХ).
Необходимая АФЧХ разомкнутой системы может быть получена следующим образом. В выражении передаточной функции разомкнутой системы W (p) заменяют p на jω и получают уравнение АФЧХ разомкнутой системы W (jω). Чтобы построить АФЧХ, необходимо представить ее состоящей из вещественной и мнимой частей:
,
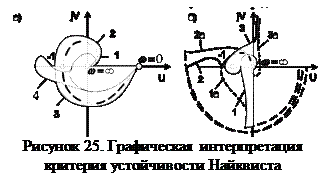затем, задаваясь значениями w от 0 до ¥: w = 0, w1 , w2,… необходимо найти точки [ U (0), jV (0)]; [ U (ω1), jV (w1)]; [ U (ω 2), jV (ω2)];…, по которым построить АФЧХ на комплексной плоскости (рис. 25).
Если разомкнутая система статическая (не имеет интегрирующих звеньев), то при w = 0 ее АФЧХ начинается на вещественной оси в точке U (0) = k, где k – коэффициент передачи разомкнутой системы. Заканчивается АФЧХ при ω = ¥ в начале координат (рис.25,а).
Если система является астатической (имеет интегрирующие звенья), то ее АФЧХ начинается при ω = 0 в бесконечности, поскольку в знаменателе амплитудно-фазовой функции W (jω) имеется множитель (jw) r, где r – порядок астатизма. Соответственно при r = 1 характеристика W (jω) при ω = 0 уходит в бесконечность вдоль отрицательной мнимой полуоси, при r = 2 – вдоль отрицательной действительной полуоси, а при r = 3 – вдоль положительной мнимой полуоси (рис. 25,б).
Разомкнутая система может быть устойчивой и неустойчивой. Критерий Найквиста для первого случая формулируется так: если разомкнутая система устойчива или находится на границе устойчивости, то для того, чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы при изменении ω от 0 до ¥ не охватывала точку с координатами (-1, j0).
На рисунке 25,а - характеристика 1 и 4 соответствуют устойчивым системам, характеристика 3 – неустойчивой, а характеристика 2 – нахождению системы на границе устойчивости. Если, например, уменьшить коэффициент передачи в неустойчивой системе, то ее АФЧХ будет «сжиматься» к началу координат, в результате чего система станет устойчивой. При увеличении коэффициента передачи характеристика ранее устойчивой системы в конце концов охватит точку (-1, j0) и система потеряет устойчивость.
Для суждения об устойчивости астатической системы, находящееся в бесконечности, начало ее АФЧХ, соответствующее ω = 0, надо мысленно соединить с положительной действительной полуосью против часовой стрелки дугой бесконечного радиуса (рис. 25,б). В случае устойчивой системы точка (-1, j0) не должна охватываться АФЧХ, мысленно дополненной дугой, соединяющей ее с положительной действительной полуосью. На рисунке 25,б сплошные кривые 1, 2, 3 относятся к устойчивым, а штриховые кривые 1а, 2а, 3а – к неустойчивым системам с астатизмом соответственно 1-го, 2-го и 3-го порядков.
В соответствии с критерием Найквиста об устойчивости можно судить не только по АФЧХ, но и совместно по АЧХ и ФЧХ разомкнутой системы. Обычно при этом пользуются логарифмическими характеристиками из-за простоты их построения. Применительно к логарифмическим характеристикам критерий устойчивости Найквиста для систем, устойчивых в разомкнутом состоянии, сводится к тому, что ЛАЧХ должна пересечь ось абсцисс раньше, чем фаза, спадая, окончательно перейдет за значение 
, т.е. на частоте среза ω с фаза должна быть меньше .
На рисунке 26 кривые 1, 2 и 4 соответствуют замкнутой устойчивой системе, ЛФЧХ, показанная пунктирной линией, соответствует нахождению замкнутой системы на границе устойчивости, ЛФЧХ 3 – неустойчивой замкнутой системе.
При оценке устойчивости систем необходимо определить запас устойчивости, т.е. степень удаленности системы от границы устойчивости. Система, которая теоретически является устойчивой, но находится очень близко к границе устойчивости, практически при ее реализации может оказаться неустойчивой вследствие неточности математического описания системы, использованного при оценке устойчивости или из-за изменения параметров системы.
В случае применения критерия Гурвица о запасе устойчивости можно судить по тому запасу, с которым выполняются входящие в этот критерий неравенства.
При использовании критерия Михайлова и Найквиста запас устойчивости определяется удаленностью соответствующих характеристик от критического положения, при котором система находится на границе устойчивости. Для критерия Михайлова это будет удаленность годографа D (jω) от начала координат, а для критерия Найквиста – удаленность характеристики W (jω) от точки c координатами (-1, j0).
В качестве меры запаса устойчивости используется запас устойчивости по фазе φ и запас устойчивости по амплитуде h (рис. 26).
Запас устойчивости по фазе определяется величиной φ, на которую должно возрасти запаздывание по фазе в системе на частоте среза ω с, чтобы система оказалась на границе устойчивости.
Запас устойчивости по амплитуде определяется величиной h допустимого увеличения АЧХ, при котором система окажется на границе устойчивости. Запас по амплитуде представляет собой запас по коэффициенту передачи k разомкнутой системы по отношению его к критическому по устойчивости значению.
При проектировании САУ рекомендуется выбирать φ ≥ 300, а h ≥ 6 дБ, что соответствует примерно двойному запасу коэффициента передачи по устойчивости.
Дата публикования: 2014-10-23; Прочитано: 5566 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
