 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Частотные характеристики звена
|
|
Частотными характеристиками называются формулы и графики, характеризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме.
Если на вход звена подается величина (рис. 10) x (t) = sin ωt, то на выходе в установившемся режиме получается: y (t)= A (ω)∙sin(ωt+ φ), где A (ω) - амплитуда, φ (ω) - фаза.
Применяется символическая запись синусоидальных колебаний:
.
Подставив эти величины в уравнение звена, получим:
,
откуда:
В результате находим:
; 
.
W (jω) = A (ω)∙e jφ (ω) представляет собой амплитудно-фазовую частотную характеристику звена (АФЧХ). Иногда W (jω) называют частотной передаточной функцией звена, которая является комплексной функцией от действительной переменной ω.
A (ω) называется соответственно амплитудно-частотной характеристикой звена (АЧХ), а φ (ω) - называется фазовой частотной характеристикой звена (ФЧХ).
Функцию W (jω) можно представить в виде:
,
где U (ω) и V (ω) – соответственно вещественная и мнимая частотные характеристики.
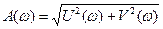
Графически АФЧХ (рис. 11) изображается на комплексной плоскости в полярных координатах A (ω), φ (ω) как годограф функции W (jω):
Длина вектора равна A (ω), а угол, образованный этим вектором с действительной положительной полуплоскостью, равен φ (ω).
Кроме частотных характеристик используются логарифмические частотные характеристики - логарифмические амплитудно-частотные (ЛАЧХ) и логарифмические фазовые частотные (ЛФЧХ) характеристики.
ЛАЧХ - это график зависимости L (w) = 20∙lg A (w) от логарифма частоты lg w. При построении ЛАЧХ по оси абсцисс откладывают частоту в логарифмическом масштабе, а по оси ординат L (w).
ЛФЧХ - это график зависимости фазовой частотной функции φ (ω) от логарифма частоты lg w. При его построении по оси абсцисс откладывают частоту в логарифмическом масштабе, по оси ординат откладывают φ (ω) в градусах или радианах.
За единицу масштаба (рис. 12) по оси абсцисс принимается декада – частотный интервал, соответствующий изменению частоты в 10 раз. В декаде содержится 3,32 октавы. Октавой называется частотный интервал, соответствующий удвоению частот, т.е. изменению частоты в 2 раза. Ось ординат при построении этих характеристик проводят через произвольную, удобную для рассматриваемой задачи точку, а не через точку w = 0, поскольку частоте w = 0 соответствует бесконечно удаленная точка.
Единицей L (w) является децибел (дБ), равный одной десятой Бела. Бел - это единица десятичного логарифма коэффициента усиления мощности сигнала, т.е. один Бел соответствует усилению мощности в 10 раз. Поскольку мощность сигнала пропорциональна квадрату амплитуды, а lg A2= 2∙lg A, то усиление в Белах, выраженное через отношение амплитуд, равно 2∙lg A. L (w) = 20 дБ означает, что на данной частоте при прохождении сигнала через звено его амплитуда увеличивается в 10 раз.
2.3. Типовые звенья САУ и их характеристики
Передаточная функция звена в общем случае представляет собой отношение двух полиномов:
Полином произвольного порядка можно разложить на простые множители k1p; (d1p+d2); (d1p2+d2p+d3), поэтому передаточную функцию можно представить как произведение простых множителей или простых дробей вида:
; 
; 
.
Звенья, передаточные функции которых имеют вид простых множителей или простых дробей, называют типовыми или элементарными звеньями. Элементарные множители, представляющие собой полиномы первого и второго порядка, преобразовываются к стандартному виду, принятому в теории автоматического управления:
; 
,
где:
· k (k > 0) - коэффициент передачи,
· T (T > 0) - постоянная времени (имеет размерность единицы времени),
· x - коэффициент демпфирования (затухания).
Основные типы звеньев делятся на: позиционные, дифференцирующие и интегрирующие.
Позиционными з веньями называются такие звенья, в передаточной функции которых многочлены M (p) и N (р) имеют свободные члены.
У дифференцирующих звеньев в передаточной функции отсутствует свободный член числителя, т.е. для однократно дифференцирующих звеньев передаточная функция имеет вид:
, где M1 (p) - свободный член.
У интегрирующих звеньев в передаточной функции отсутствует свободный член знаменателя, т.е.:
.
1. Апериодическое звено. Стандартная форма записи уравнения звена: 
Апериодическими звеньями являются RC и RL цепи, входные и выходные величины которых показаны соответственно на рисунке 13, а и 13, б.
В операторной форме напряжение и ток на выходе для схемы (рис. 13, а) соответственно равны:
и 
Тогда:
.
Передаточная функция апериодического звена:
,
В общем случае передаточная функция апериодического звена имеет вид:
где: k = 1, T = RC.
Переходная функция апериодического звена (рис. 14,а):
.
Весовая функция апериодического звена (рис. 14,б):
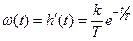
Если характеристики этих функций получены экспериментально, по ним можно определить значения T и k и получить уравнение звена. За длительность переходного процесса принимают время, в течение которого выходная величина достигает 95% ее конечного значения.
Амплитудно-фазовая частотная характеристика (АФЧХ) апериодического звена (рис. 14,в):
,
где: 
, 
.
Эта характеристика представляет собой полуокружность с радиусом k /2 и центром с координатами (k /2; j = 0) на действительной оси.
Амплитудно-частотная (АЧХ) апериодического звена:
Фазовая частотная характеристики (ФЧХ) апериодического звена:
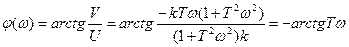
Логарифмическая амплитудная частотная характеристика (ЛАЧХ) апериодического звена (рис. 14,г):
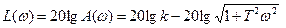
Приближенно ЛАЧХ можно заменить двумя асимптотами, к которым она стремится при w → 0 и w → ¥. Приближенная ЛАЧХ называется асимптотической.
· при малых значениях w << 1/ T, → 
, т.е. L (w) = 20lg k - в этом случае ЛАЧХ представляет собой прямую, параллельную оси абсцисс и проходящую на уровне 20lg k.
· на больших частотах, когда w >> 1/ T, →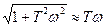 
, т.е. L (w) = 20lg k - 20lg Tw - в этом случае характеристика представляет собой прямую имеющую наклон минус 20 дБ/дек.
Обе асимптоты пересекаются в точке, соответствующей w = 1/ T. Эта частота называется сопрягающей.
На фазовой частотной характеристике (ФЧХ) при w → ¥ значение φ изменяется от 0 до минус π/2.
2. Колебательное звено. Уравнение колебательного звена имеет вид: 
.
Оно представляет собой последовательное соединение RLC элементов (рис. 15).
В операторной форме напряжение на выходе колебательного звена:
, где: 
, 
.
Принято обозначать Т0 = Т, Т1 = 2ξТ, тогда передаточная функция колебательного звена имеет вид:
,
Коэффициент ξ (дзета) называется коэффициентом демпфирования (затухания). Если 0 < ξ < 1, звено называется колебательным; если ξ = 0 (Т1 = 0), звено называется консервативным, если ξ ≥ 1 - апериодическим звеном второго порядка.
Апериодическое звено второго порядка можно представить как последовательное соединение двух апериодических звеньев первого порядка. Оно не относится к числу элементарных звеньев.
В общем случае амплитудно-фазовая частотная характеристика звена (рис. 16,а):
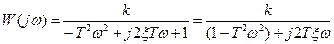где k = 1.
Умножив числитель и знаменатель на комплексно сопряженное знаменателю выражение, получим:
,
Отсюда вещественная и мнимая частотные характеристики колебательного звена:
и 
Амплитудно-частотная характеристика колебательного звена (АЧХ):
Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) колебательного звена:
.
При малых значениях частоты ω<1/Т = ωс в выражении 
можно пренебречь величиной Т2ω2, а при значениях частоты ω>1/Т в выражении можно пренебречь единицей и слагаемым (2ξТω)2. Тогда уравнение асимптотической ЛАЧХ колебательного звена можно записать:
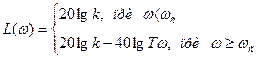
Асимптотическая ЛАЧХ (рис. 16,б) при ω<1/Т = ωс (ωс - сопрягаемая частота) параллельна оси частот, а при ω ≥ 1/Т имеет наклон минус 40 дБ/декаду. При значениях 0,5<ξ<1 характеристика близка к ломанной линии, если ξ<0,5, то получается заметный «горб», который уходит в бесконечность при ξ → 0. Роль постоянных времени Т0 и Т1 в уравнении колебательного звена следующая: постоянная Т0 - «раскачивает» колебания, а Т1 - демпфирует их.
Фазовая частотная характеристика (ФЧХ) (рис. 16,б) изменяется монотонно в интервале от 0 до -p:
Переходная функция колебательного звена (рис. 16,в) при нулевых начальных условиях:
,
где: 
; 
; 
.
При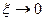 
переходная характеристика представляет собой график гармонических колебаний.
Весовая функция колебательного звена:
3. Интегрирующее звено. Уравнение идеального интегрирующего звена имеет вид:
Идеальными интегрирующими звеньями являются цепи с элементами C и L (рис. 17). В первом случае входной величиной x является ток заряда конденсатора, а напряжение на нем – выходной величиной y. Во втором случае входной величиной x является напряжение на индуктивности, а ток – выходной величиной y.
Отличительным свойством интегрирующего звена является то, что после прекращения действия входного сигнала х выходной сигнал звена у остается на том уровне, на котором был в момент исчезновения входного сигнала. Иначе говоря, интегрирующее звено обладает свойством «запоминать» последнее значение выходной величины. Благодаря «памяти» интегрирующего звена достигается астатизм автоматической системы.
В операторной форме уравнение интегрирующего звена:
.
Передаточная функция интегрирующего звена:
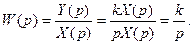
Амплитудно-фазовая частотная характеристика (АФЧХ) интегрирующего звена (рис. 18,а):
,
Вещественная и мнимая частотные характеристики имеют вид:
, 
.
Амплитудно-частотная характеристика (АЧХ) интегрирующего звена:
.
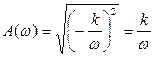Уравнение асимптотической ЛАЧХ интегрирующего звена (рис.18,б):
.
Асимптотическая ЛАЧХ (рис. 18,б) представляет собой прямую, проходящую через точку 20∙lg k при w = 1 с наклоном минус 20 дБ/дек.
Логарифмическая фазовая частотная характеристика (ЛФЧХ) интегрирующего звена:
Переходная характеристика интегрирующего звена (рис. 18,в):
Весовая функция интегрирующего звена:
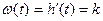
Реальные интегрирующие зв енья являются инерционными. Их передаточная функция имеет вид:
Характеристики реального интегрирующего звена можно получить, представив его как последовательное соединение идеальных интегрирующего и апериодического звеньев.
4. Дифференцирующее звено. Уравнение идеального дифференцирующего звена: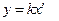 
Идеальными дифференцирующими звеньями являются цепи с конденсатором и элементом индуктивности (рис. 19). Входной величиной x в первом случае является напряжение, а во втором - ток. Выходной величиной y в первом случае является ток, а во втором - напряжение.
В операторной форме уравнение дифференцирующего звена имеет вид:
.
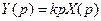Уравнение передаточной функции дифференцирующего звена:
Амплитудно-фазовая частотная характеристика (АФЧХ) дифференцирующего звена:
,
Вещественная и мнимая частотные характеристики имеют вид (рис.20,а):
, 
Амплитудно-частотная характеристика (АЧХ) дифференцирующего звена:
.
Уравнение асимптотической ЛАЧХ дифференцирующего звена:
.
Асимптотическая ЛАЧХ (рис. 20,б) представляет собой прямую, проходящую через точку 20lg k при w = 1 с наклоном плюс 20 дБ/дек.
Выражение для логарифмической фазовой частотной характеристики (ЛФЧХ) дифференцирующего звена:
Переходная характеристика дифференцирующего звена:
Весовая функция дифференцирующего звена:
где δ – дельта-функция (производная от единичной функции): 
,
Реальные дифференцирующие звенья являются инерционными. Передаточная функция такого звена:
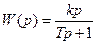
Характеристики реального дифференцирующего звена можно получить представив его, как последовательное соединение идеальных дифференцирующего и апериодического звеньев.
Дата публикования: 2014-10-23; Прочитано: 14739 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
