Тесты для самопроверки. 1. В зависимости от базы сравнения индексы подразделяются на:

1. В зависимости от базы сравнения индексы подразделяются на:

а) динамические;

б) индивидуальные;

в) групповые;

г) территориальные;

д) сводные.

2. В зависимости от степени охвата элементов совокупности индексы делятся на:

а) индивидуальные;

б) динамические;

в) общие;

г) объема;

д) территориально-пространственные.

3. Индивидуальный индекс показывает соотношение между:

а) отчетным и базисным показателями;

б) индивидуальным и сводным индексами;

в) цепным и базисным расчетом показателя;

г) индексируемой величиной и весом.

4. Индивидуальные индексы являются относительными величинами:

а) сравнения;

б) динамики;

в) структуры;

г) координации.

5. Концепциями индексной теории являются:

а) общий индекс;

б) синтетическая;

в) пространственный;

г) аналитическая.

6. Общие индексы характеризуют относительное изменение показателя в целом по:

а) территориальному округу;

б) отдельному элементу сложной совокупности;

в) сложной совокупности;

г) всем весам индексов.

7. Объем выпуска продукции по отрасли относится к индексам:

а) индивидуальному;

б) общему;

в) пространственному;

г) синтетическому.

8. К субиндексам относятся:

а) групповые;

б) цепные;

в) динамические;

г) аналитические.

9. Индекс переменного состава цены отражает динамику среднего показателя для:

а) разнородной совокупности;

б) территориально-пространственной совокупности;

в) однородной совокупности;

г) частной совокупности.

10. Метод Уолша[lxxvii] применяется для расчета сопоставлений:

а) двух пространственно-территориальных совокупностей

б) многосторонних сопоставлений;

в) сравнения индивидуальных индексов;

г) сравнения средних индексов.

11. Индекс фиксированного состава качественных показателей дает тот же результат, что и:

а) агрегатный индекс потребления;

б) индекс ассортиментных сдвигов;

в) индекс цены Пааше;

г) цепной индекс цены.

12. Если рассчитать отношение абсолютного прироста на относительный прирост одного и того же показателя, то можно получить:

а) абсолютное значение 1% прироста;

б) сумму цепных приростов;

в) характеристику базисного индекса;

г) произведение цепных индексов.

13. Постоянные веса в индексах позволяют:

а) исключить влияние изменения структуры на величину индекса;

б) оценить влияние изменения структуры;

в) рассчитать цепные индексы;

г) усилить влияние изменения структуры.

14. Какова внешняя отличительная особенность любого агрегатного индекса:

а) числитель и знаменатель представляют собой сумму произведений двух показателей одного временного периода;

б) числитель и знаменатель представляют собой сумму произведений двух показателей разного временного периода;

в) числитель и знаменатель представляют собой сумму произведений двух показателей, один из которых является индексируемой величиной, а второй остается неизменным;

г) числитель и знаменатель представляют собой сумму произведений двух показателей, когда оба являются индексируемыми величинами.

15. Разность D pq = å p ₁ q ₁ – å p ₀ q ₁ представляет собой прирост:

а) выручки за счет изменения цены в среднем;

б) выручки за счет средней цены;

в) выручки за счет ассортимента;

г) выручки за счет структуры.

16. Можно ли при построении индекса потребления использовать кроме цены такие соизмерители, как:

а) себестоимость;

б) трудоемкость;

в) урожайность;

г) площадь территории?

17. Можно ли суммировать цены различных товаров:

а) да;

б) нет;

в) с определенной вероятностью;

г) с определенной погрешностью.

18. Какие индексы могут быть использованы для изучения состава явления:

а) переменного и фиксированного состава;

б) средний арифметический и средний гармонический;

в) индексы количественных и качественных показателей;

г) агрегатные и пространственно-территориальные?

19. По периоду исчисления индексы подразделяются на:

а) количественные и качественные;

б) годовые, квартальные, месячные, недельные;

в) по отдельным предприятиям и отраслевые;

г) индексы из средних величин и агрегатные.

20. По объекту исследования индексы могут быть:

а) агрегатные;

б) индексы из средних величин;

в) производительности труда, себестоимости, физического объема;

г) индексы динамические и пространственно-территориальные.

21. Показателем инфляции является:

а) индекс потребления;

б) индекс цены;

в) индекс структурных сдвигов;

г) индекс выручки.

22. Индекс Струмилина[lxxviii], используемый при анализе производительности труда, является:

а) агрегатным индексом;

б) средним гармоническим индексом;

в) индексом переменного состава;

г) средним арифметическим индексом.

23. Индекс Доу-Джонса[lxxix] определяется на основе значений курсов акций как индекс:

а) средний арифметический;

б) средний геометрический;

в) средний гармонический;

г) средний из базисных индексов.

24. Индекс себестоимости переменного состава, равный 1,0098, характеризует:

а) увеличение средней отраслевой себестоимости на 0,98% в текущем периоде по сравнению с базисным;

б) уменьшение средней отраслевой себестоимости на 1,0098%;

в) увеличение средней отраслевой себестоимости на 0,98% за счет вариации себестоимости на отдельных предприятиях, входящих в данную отрасль;

г) увеличение средней отраслевой себестоимости на 0,98% за счет факторного ресурса.

25. Метод стандартных весов применяется при построении:

а) агрегатных индексов;

б) средних индексов;

в) пространственно-территориальных индексов;

г) индексов из средних величин.

26. Система цепных индексов применяется при изучении динамики последовательно вычисленных индексов:

а) одного и того же явления с постоянной базой сравнения;

б) одного и того же явления с меняющейся от индекса к индексу базой сравнения;

в) различных явлений с постоянной базой сравнения;

г) различных явлений с меняющейся от индекса к индексу базой сравнения.

27. По четырем группам товаров текущий товарооборот магазина составил 67, 52, 138 и 214 млн руб. По первой группе цены не изменились, по второй группе цены выросли на 7,1%, по третьей группе цены выросли на 4,7%, а по четвертой группе снизились на 8,7 %. Определить общий индекс цен:

а) 0,9777;

б) 1,0228;

в) 1,0078;

г) решения нет.

28. Индекс цен на продовольственные товары за год составил 118%, на непродовольственные товары — 105,7%, на платные услуги — 116,3%. Рассчитать ИПЦ, если известно, что продовольственные товары составили 45%, непродовольственные товары — 30%, а платные услуги — 25%:

а) 1,1333;

б) 0,3149;

в) 1,1389;

г) решения нет.

29. Затраты на производство продукции за текущий год увеличились на 18%, себестоимость единицы продукции при неизменной структуре производства увеличилась на 3%, выпуск продукции увеличился на 5%. Требуется определить влияние структурных изменений на выпуск продукции:

а) 0,9427;

б) 1,0608;

в) 1,1124;

г) решения нет.

Приложение 1. Математико-статистические таблицы и их практическое применение[3]

В статистической[lxxx] науке широко применяются математико-статистические таблицы, которые необходимы при решении различных задач. Ниже описаны таблицы, показано их практическое применение к решению как социально-экономических задач, так и задач в других областях. Собственно таблицы приведены в приложении 2. В нахождении числовых характеристик по таблицам очень часто требуется знание числа степеней свободы, поэтому дадим некоторые разъяснения. Число степеней свободы — количество вариантов, могущих принимать значения, функционально не связанные друг с другом. Для вариационного ряда число степеней свободы вариации равно числу групп минус число исчисленных при расчете теоретического распределения характеристик (средняя, дисперсия и т.д.).

В дисперсионном анализе число степеней свободы определяется при исчислении различных дисперсий и равно при расчете: 1) общей дисперсии, т.е. дисперсии комплекса k_y = n – 1 (число значений варьирующего признака без одного); 2) факторной дисперсии k_F = r – 1 (число групп без одной); 3) остаточной (случайной) дисперсии k_z = n – r (число значений варьирующего результативного признака без числа групп). Следует иметь в виду, что в представленных таблицах обозначения степеней свободы разнятся, это надо учитывать при нахождении того или иного значения по таблицам.

Таблица П2.1. Степени натуральных чисел.

Данная таблица призвана для проведения арифметических расчетов, когда требуется быстрое получение ответа, а у аналитика нет компьютера или калькулятора.

Таблица П2.2. Таблица расчета средних темпов роста.

Таблица расчета средних темпов роста применяется при необходимости получения обобщающей характеристики средних темпов роста и прироста, когда у аналитика нет компьютера или калькулятора.

Таблица П2.3. Значения некоторых функций, часто встречающихся в статистических вычислениях.

Таблица удобна при выполнении статистических вычислений.

Таблица П2.4. Таблица случайных чисел.

Таблица случайных чисел применяется при необходимости проведения случайного отбора единиц совокупности и если выборочная совокупность имеет большой объем. В этой таблице представлены серии цифр, набранные случайным образом при помощи специального прибора. Вероятность появления любой цифры составляет 1/10, поскольку в мире применяется десятичная цифровая система. Для удобства восприятия человеческого глаза и лучшей обозримости цифры сгруппированы по пять единиц.

Пример П1.1. Допустим, что необходимо из 4000 предприятий города (генеральная совокупность) отобрать 5% предприятий для обследования, т.е. 200 предприятий.

Решение

Число, характеризующее генеральную совокупность (4000), является четырехзначным, поэтому код каждого предприятия будет четырехзначным, от 0001 до 4000. Для начала отбора выбирается начальная точка, которую можно получить любым способом, например, закрыв глаза, поставить точку на любое число в таблице, и с этого места (точки) начинается отсчет 200 единиц. Процедура отбора единиц может проходить по строчкам таблицы либо по колонкам. Поскольку в таблице пятизначные числа, то отбрасывается либо первая, либо последняя цифра и отбираются числа, не превышающие число единиц в генеральной совокупности (4000).

Пусть точка на таблице случайных чисел попала на 47 строчку в первый столбец. Тогда для отбора отбрасываем первую цифру и получаем ряд из четырех чисел: 2167, числа 8940 и 7149 отбрасываем, 0242, 0587, далее 9786, 4959, 5339, 7864 — отбрасываем, поскольку наше максимальное число 4000, 0991 и т.д. пока не будет набрано 200 единиц.

Можно проводить механический отбор единиц с шагом, равным (N/n). В рассматриваемом примере 4000/200 = 20, т.е. каждая двадцатая цифра отбирается в выборочную совокупность. Начало отсчета желательно начинать с середины шага, в этом случае гарантируется несмещенность выборки. Отбор единиц в выборочную совокупность будет проводиться аналогично тому, как в первом случае, но будет соблюдаться рассчитанный шаг.

Пример П1.2. Каковы будут номера единиц, попавших в выборку, если генеральная совокупность состоит из 400 единиц, и в соответствии с программой выборки должно быть обследовано 50 единиц?

Решение

Допустим, совершенно случайно берем первый столбик таблицы и в соответствии с условием отбираем 50 данных: 194, 240 (число 833 не берем, поскольку единицы с таким номером в генеральной совокупности нет), 111, 189, 396 и т.д.

5. Таблица П2.5. Значения функции .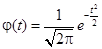

Данная таблица используется при расчете теоретических частот кривой нормального распределения.

Алгоритм расчетов следующий.

1. Рассчитывается средняя арифметическая величина 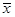и среднее квадратическое отклонение s на основе имеющихся данных.

2. Определяется нормированное отклонение (t_i) каждого варианта от средней арифметической: .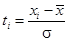

3. По таблице распределения функции 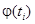определяются ее значения.

4. Вычисляются теоретические частоты 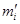по формуле 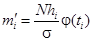, где N — объем совокупности; h_i — величина интервала.

Пример П1.3. Имеются данные о прибыли (млн руб.) по 210[lxxxi] предприятиям области (табл. П1.1, первые два столбца). Требуется рассчитать теоретические частоты.

Таблица П1.1

Данные для примера П1.3

Прибыль	Число предприятий	xi	ximi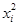
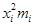
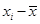
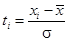
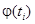
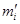
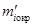
1—3						–4,65	1,93	0,0620	6,95
3—5						–2,65	1,099	0,2203	24,68
5—7						–0,65	0,269	0,3847	43,10
7—9						1,35	0,560	0,3410	38,20
9—11						3,35	1,390	0,1518	17,00
Итого		—		—		—	—	—	—

Решение

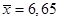млн руб.; ; ;

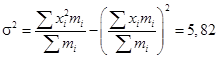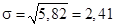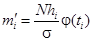= 112,03.[lxxxii]

Задача П1.1. Имеются следующие данные о выпуске продукции по предприятиям города (табл. П1.2).

Таблица П1.2

Данные для задачи П1.1

Выпуск продукции (тыс. руб.)	Число предприятий
10—30
30—50
50—70
70—90
90—110
110—130
Итого

Требуется рассчитать теоретические частоты.

6. Таблица П2.6. Распределение Пуассона 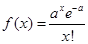(закон распределения редких явлений)

Распределение Пуассона наблюдается в совокупностях большого объема (более 100 единиц) и является результатом редко возникающих событий. Например, гибель от удара копытом лошади, появление в квартире шаровой молнии и т.д. Данное распределение имеет некоторые особенности: значения признака носят дискретный характер, доля единиц, обладающих большими значениями признака, мала (например, у одной и той же машины одновременно найдено 18 неисправностей), с увеличением значений признака вероятность наступления события падает.

Расчет теоретических частот кривой распределения Пуассона следующий.

1. Определяется средняя арифметическая величина .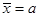

2. По таблицам находится .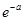

3. Для каждого значения x_i рассчитывается теоретическая частота по формуле 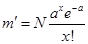, где N — число единиц в данной совокупности.

Как очевидно из сказанного, данное распределение используется в теории массового обслуживания, т.е. применяется при необходимости расчета числа заявок, поступающих в систему массового обслуживания, например на телефонные станции, в ремонтные мастерские, торговые предприятия, для описания числа отказов технологического оборудования в единицу времени.

Пример П1.4. Изучается качество производимого оборудования «А», для чего были изучены неисправности на 790 единицах. Результаты обследования представлены в табл. П1.3[lxxxiii].

Таблица П1.3

Данные для примера П1.4

Число неисправностей							Итого
Количество единиц оборудования

Решение

Рассчитываются средняя арифметическая и дисперсия: 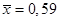, s² = 0,9881. Поскольку эти показатели по своим характеристикам относительно близки, а также в данном распределении существует увеличение значений признака при уменьшении частоты, то весьма вероятен вывод, что данное распределение относится к пуассоновскому. Имеем 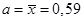. По таблице определяется 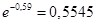и рассчитываются теоретические частоты: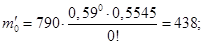

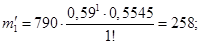
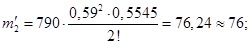
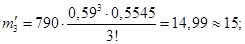
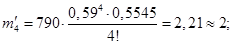
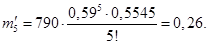
Сумма теоретических частот: .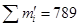

Задача П1.2. Имеются данные о числе заявок на телефонные разговоры (табл. П1.4).

Таблица П1.4

Данные для задачи П1.2

Телефонные разговоры в единицу времени									Итого
Число заявок

Требуется рассчитать теоретические частоты для изучения распределения числа заявок на телефонные разговоры в единицу времени и провести статистическую проверку на расхождение теоретических и эмпирических данных, используя критерий c² Пирсона.

7. Таблица П2.7. Значение интеграла вероятностей .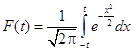

Применяется при выявлении закономерностей распределения, определении характера нахождения изменений в распределении, вероятностей, достоверности коэффициента регрессии в малых совокупностях и при решении других задач. Например, при определении пределов характеристик генеральной совокупности при проведении выборочных исследований. В таблице приведены значения интеграла Лапласа для разных t (коэффициентов доверия). Коэффициенты доверия t приведены в первой колонке таблицы, в остальных колонках (столбцах) таблицы значатся значения площадей.

Площадь, ограниченная кривой нормального распределения и осью абсцисс, равна единице, или 100%.Часть площади, находящаяся в пределах – t до + t равна 0,683, иначе говоря, с вероятностью, равной 0,683, можно гарантировать, что отклонение генеральной средней или доли от выборочных оценок не превысит однократной ошибки выборки.

Площадь, находящаяся в пределах ±2 t равна 0,954, или 95,4%, в случае изучения площади, равной 0,997 (±3 t) можем констатировать, что оценки генеральной средней величины или доли не выйдут за заданные пределы.

Для ограниченного числа наблюдений параметры не являются единственно возможными, они дают лишь оценку параметров связи в генеральной совокупности. Поэтому необходимо определить среднюю ошибку и с заданной вероятностью пределы, в которых могут находиться параметры связи. Далее параметры проверяются на существенность.

Расчет ошибок параметров a и b [lxxxiv] основан на использовании остаточного среднего квадратического отклонения 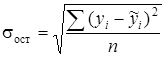. Средняя ошибка параметра a: 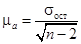. Средняя ошибка коэффициента регрессии определяется по формул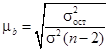е , где 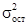— остаточная дисперсия; s² — общая дисперсия, 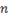— число коррелируемых пар.

Пример П1.5. Допустим, изучается зависимость между возрастом и производительностью труда. Получено уравнение регресси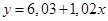и при 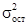= 0,28 и s² = 1,1. Изучаемая совокупность равна 52 сотрудникам, коэффициент регрессии, равный 1,02, подвержен случайным колебаниям, и требуется проверить его достоверность, рассчитав среднюю ошибку.

Решение

Вычисляем 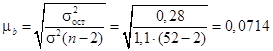. Предельная ошибка коэффициента регрессии 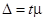при заданной вероятности 0,954 и t = 2 равна ±0,1427, т.е. 1,02±0,1427. Итак, коэффициент регрессии b будет находиться в пределах не менее 0,8773 и не более 1,1627 с гарантированной вероятностью 0,954.

Далее проверяется значимость параметров регрессии путем соотношения значения параметров с его средней ошибкой. Поскольку коэффициент регрессии показывает, на сколько в абсолютном выражении изменяется значение результативного признака y при изменении факторного признака x на единицу, изучение его значимости особенно полезно. Рассчитав по формуле 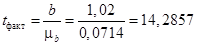, можно сделать вывод, что поскольку 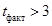, это свидетельствует о значимости коэффициента регрессии.

В малых совокупностях значение коэффициента регрессии подвержено случайным колебаниям, что вызывает необходимость в определении достоверности и значимости коэффициента регрессии. Его достоверность определяется так же, как и в выборочном наблюдении, т.е. устанавливается средняя и предельная ошибки для выборочной средней и доли.

В случае если выборка менее 30 наблюдений, то 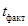сопоставляется с 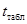(критическим) t -критерием Стьюдента. Если 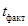> 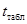, то параметр считается значимым.

Пример П1.6. Допустим, необходимо определить площадь (вероятность) при t = 1,84. Находится значение площади[lxxxv], равное 0,9342. Обратная задача: вероятности 0,8132 соответствует коэффициент доверия 1,32.

Пример П1.7. С вероятностью, равной 0,954, требуется определить предельную ошибку выборки доли детей до 7 лет, если известно, что выборочная совокупность составила 350 детей и доля детей до 7 лет равна 12%.

Решение

При вероятности 0,954 по табл. П2.7 коэффициент доверия t = 2. Предельная ошибка выборки при повторном отборе равна 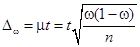. Подставляем данные: 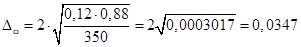, т.е. .

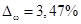Следовательно, с вероятностью 0,954 можно утверждать, что доля детей по генеральной совокупности (ее численность неизвестна) до 7 лет составила 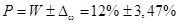, или не менее 8,53% и не более 15,47% от численности детей до 7 лет в генеральной совокупности.

Пример П1.8. Необходимо определить вероятность, с которой она[lxxxvi] может быть гарантирована, если известно, что предельная ошибка выборки составила 3%, а средняя ошибка 2,13%.

Решение

Поскольку 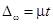, то 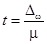, t = 3,0/2,13=1,4085, то по табл. П2.7 определяется искомая вероятность, которая равна P = 0,8415.

Пример П1.9. Обследовалось 150 предприятий. Определите долю (%) и число предприятий, оборудование которых работает от 8 до 18 часов в сутки, если среднее число работы оборудования составляет 12 часов, при наличии среднего квадратического отклонения в 2,5 часа.

Решение

Определяется нормированное отклонение — значения t ₁ и t ₂:

; .

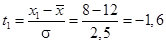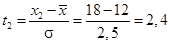По таблице значений интеграла вероятностей Лапласа находится вероятность (P):

; .

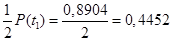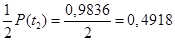Общая характеристика 0,4452 + 0,4918 = 0,9370. Доля предприятий, имеющих оборудование, которое работает от 8 до 18 часов, составляет 93,70%, а их численность — 1405 предприятий.

Задача П1.3. В ходе проведения опроса200 сотрудников было выявлено, что средний возраст работающих составляет 30 лет. Определите число сотрудников в возрасте от 28 до 35, если коэффициент вариации равен 16%.

Задача П1.4. В результате выборочного исследования 180 студентов (2%) на предмет их успеваемости имеются следующие данные (табл. П1.5).

Таблица П1.5

Данные для задачи П1.4

Балльная оценка	Число студентов
А
В
С
D
E
F
Итого

Требуется с вероятностью 0,954 определить пределы, в которых находится: а) средняя бальная оценка по всему образовательному учреждению; б) долю студентов имеющих оценки D и E.

Задача П1.5. Имеются выборочные данные о возрасте и выработке рабочих предприятия (табл. П1.6).

Таблица П1.6

Данные для задачи П1.5

Возраст рабочих предприятия	Выработка на одного рабочего (шт.)

Изучите взаимосвязь между названными факторами, рассчитайте уравнение регрессии, определите достоверность и значимость коэффициентов регрессии.

8. Таблица П2.8. S (t) в распределении [lxxxvii] Стьюдента.

Таблица применяется в случаях использования малых выборок. В таблице представлены вероятности S (t), находящиеся на пересечении значений t и n — степеней свободы. S (t)— это вероятность, характеризующая фактическое значение нормированного отклонения выборочной средней (либо доли) от генеральной, оно будет не больше, чем табличное значение. Выводы, сделанные на основе малой выборки, считаются справедливыми лишь при нормальном распределении значений изучаемого признака в генеральной совокупности.

Пример П1.10. В результате выборочного исследования 15 предприятий оказалось, что средняя доля старого оборудования составляет 14%. Определите вероятность того, что в генеральной совокупности доля старого оборудования не превысит 20%.

Решение

Последовательность действий такова.

1. Предельная ошибка доли рассчитывается по формуле 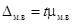[lxxxviii]. По условию задачи в генеральной совокупности доля оборудования составляет 20% (P = 20%); в выборочной совокупности — W = 14%, поэтому предельная ошибка доли составит 6% (0,06).

2. Выборочная дисперсия .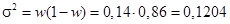

3. Средняя ошибка выборочной доли .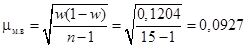

4. Определяем коэффициент доверия: .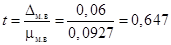

5. При n = 14 и t = 0,647 S (t) = 0,7365, т.е. с достоверностью 73,65% можно утверждать, что доля старого оборудования в генеральной совокупности не превысит 20%.

Пример П1.11. При проведении выборочного исследования 10 магазинов оказалось, что в среднем величина между весом продуктов, отпускаемых покупателям, и проверочным весом составляет 23 г при среднем квадратическом отклонении 12 г. С вероятностью 0,95 определите по генеральной совокупности пределы, в которых находится средний вес продуктов, отпускаемый покупателям.

Решение

Поскольку совокупность n < 30, то 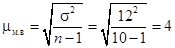г.

Так как P (t) = 0,95, то 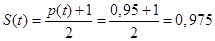. Поскольку n = 10 – 1 = 9, то значение t находится между 2,2 и 2,3. Более определенно величину t можно найти по табл. П.2.9, где при n = 9 и a = 0,05 t = 2,2622. Поэтому предельная ошибка выборки 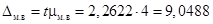г. Пределы разницы веса для генеральной совокупности: 23 ± 9,0488 г.

Задача П1.6. В результате выборочного исследования 12 предприятий оказалось, что средняя доля активных фондов составила 36%. Определите вероятность того, что в генеральной совокупности доля активных фондов не превысит 41%.

9. Таблица П2.9. Значение t -критерия Стьюдента при уровне значимости 0,10, 0,05, 0,01.

Распределение Стьюдента применяется при наличии малых совокупностей. Теория малых выборок была разработана английским статистиком В. Госсетом, взявшим себе псевдоним Стьюдент.

При использовании выборок объема n ≤ 30 (малые выборки) характер распределения генеральной совокупности сказывается на распределении ошибок выборки. Малые выборки применяются для решения задач, связанных с проверкой статистических гипотез. Распределение Стьюдента, как и нормальное, симметрично относительно точки t = 0, но оно значительно более пологое. Данное распределение имеет только один параметр — число степеней свободы, которое равно числу индивидуальных значений признака. Таблицы распределения Стьюдента существуют в двух вариантах: (а) как и в таблицах интеграла вероятностей, приводятся величины t и соответствующие вероятности F(t) при разном числе степеней свободы; (б) значения t приводятся для наиболее часто используемых доверительных вероятностей 0,90, 0,95 и 0,99 или при уровнях значимости 0,10, 0,05 и 0,01 при разном числе степеней свободы.

Существуют три типовых ситуации, в которых применяется критерий Стьюдента.

Ситуация 1. Проверка гипотез о средних величинах.

Пример П1.12. Для оценки влияния формы собственности на эффективное использование оборудования было проведено выборочное исследование частных и государственных предприятий, в результате получены следующие данные (табл. П1.7).

Таблица П1.7

Данные для примера П1.12

Форма собственности	Число предприятий	Средняя фондоотдача (выпуск продукции на 1 д.е. стоимости основных фондов)	Среднее квадратическое отклонение
Государственная		1,15	0,28
Частная		1,17	0,31

Требуется проверить нулевую гипотезу, что форма собственности не влияет на эффективность использования оборудования.

Решение

Имеем: 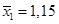, , 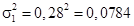n ₁ = 12; 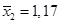, , 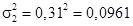n ₂ = 12.

Подставим данные в формулу[lxxxix]: .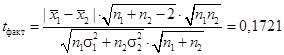

По таблице Стьюдента 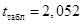при a = 0,05 и числе степеней свободы 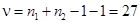. Поскольку 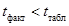, принимается нулевая гипотеза, т.е. форма собственности не влияет на эффективность использования оборудования.

Ситуация 2. Установление значимости линейного коэффициента корреляции.

Выдвигается и проверяется гипотеза о равенстве коэффициента корреляции нулю. Если 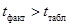, то нулевая гипотеза отвергается, что свидетельствует о значимости линейного коэффициента корреляции, следовательно, и о статистической существенности зависимости между признаками.

Для оценки значимости коэффициента парной корреляции рассчитывается фактическая величина t: 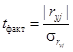, где 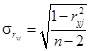. Коэффициент парной корреляции можно считать значимым, если 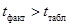при заданном уровне значимости a и числе степеней [xc]свободы .

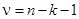При необходимости возможен расчет доверительного интервала коэффициента корреляции при заданной вероятности.

Коэффициент корреляции рассчитывается для определенного числа наблюдений и, как любой выборочный показатель, содержит случайную ошибку.

Оценку значимости, существенности коэффициента корреляции можно определить при наличии больших совокупностей (без расчета табличных значений) как отношение 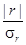. Если данное отношение больше 3, т.е. коэффициент корреляции r превышает свою среднюю ошибку более чем в три раза, данный результат считается значимым, а связь реальной. Зная величину вероятности, можно определить доверительные пределы коэффициента корреляции по генеральной совокупности.

Ситуация 3. Статистическая оценка точности и надежности параметров корреляции.

Для оценки значимости каждого коэффициентов регрессии применяется расчет t -критерия Стьюдента как отношение коэффициента регрессии к его средней ошибке: 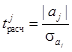. Средняя (стандартная) ошибка коэффициента регрессии определяется как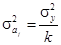 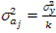, где 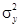— дисперсия результативного признака; 𝑘 — число факторных признаков. Коэффициент регрессии можно считать статистически значимым, если 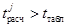при заданном уровне значимости a и числе степеней свободы .

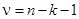Пример П1.13. Проведено выборочное обследование 50 магазинов в целях изучения взаимосвязи между площадью магазинов и их товарооборотом. Коэффициент корреляции между этим факторами оказался равным 0,762[xci].

Решение

Для получения коэффициента корреляции по генеральной совокупности была задана вероятность 0,9876. По табл. П2.7 определяется коэффициент доверия t = 2,5.

Коэффициент корреляции по генеральной совокупности находится по формуле 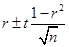. Подставляем данные: 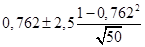. В результате расчетов имеем 0,762 ± 0,148. Коэффициент корреляции по генеральной совокупности, характеризующий связь между товарооборотом и площадью магазинов, колеблется в пределах 0,614 £ r £ 0,91.

Если совокупность менее 30 единиц, то средняя ошибка линейного коэффициента корреляции определяется по формуле .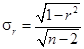

Значимость коэффициента корреляции проверяется по t -критерию Стьюдента. Проверяется нулевая гипотеза о равенстве коэффициента корреляции нулю, т.е. об отсутствии связи между x и y в генеральной совокупности. По специальной формуле находится 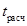, которое сравнивают с 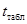. В случае если 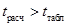нулевая гипотеза отвергается и делается вывод о существенности связи между изучаемыми факторами, если же 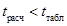, то принимается нулевая гипотеза, т.е. связь между факторами x и y отсутствует, а значение r > 0 считается, получено случайно.

Пример П1.14. Изучается взаимосвязь между урожайностью и величиной внесенных удобрений по 15 случайно выбранным участкам, т.е. n = 15 (малая совокупность). Коэффициент корреляции r оказался равным 0,836. Необходимо определить значимость коэффициента корреляции и существенность взаимосвязи между факторами.

Решение

Поскольку имеем малую совокупность — всего 15 пар данных, то применяем формулу .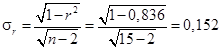

Определяем фактическое значение критерия Стьюдента: 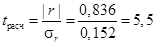. Число степеней свободы 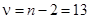, уровень значимости a = 0,05, тогда по табл. П2.9определяется .

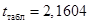Поскольку 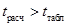(5,5 > 2,1604), то нулевая гипотеза отвергается, т.е. связь между факторами 𝑥 и y существенна, а коэффициент корреляции значим.

2. Статистическая оценка[xcii] надежности параметров парной регрессии. Коэффициент регрессии признается статистически значимым, если t _факт > t _табл, при заданном уровне значимости критерия проверки гипотезы о равенстве нулю параметров, измеряющих связь и числе степеней свободы .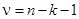

3. Оценка точности и надежности параметров множественной регрессии.

4. При использовании методики решения точно идентифицируемой системы, называемой иначе косвенным методом наименьших квадратов (КМНК).

5. При определении значимости коэффициента корреляции рангов Спирмена.

6. Применяется для оценки существенности различия среднегодовых приростов.

7. Для получения достаточно надежных границ прогноза положения тренда.

Задача П1.7. Имеются данные, характеризующие экономику предприятий (табл. П1.8).

Таблица П1.8

Данные для задачи П1.7

Номер предприятия	Средняя стоимость основного капитала (млн руб.)	Выработка на 1 рабочего (тыс. руб.)	Прибыль предприятия (млн руб.)

По данным таблицы проведите корреляционно-регрессионный анализ: постройте уравнение регрессии, проведите статистическую оценку точности и надежности параметров коэффициента корреляции, проведите анализ коэффициентов эластичности, проверьте адекватность уравнения регрессии. Напишите аналитическую записку.

10. Таблица П2.10. Значение критерия c² Пирсона при уровне значимости 0,10 0,05, 0,01 и числе степеней свободы n .

Полная и точная проверка соответствия гипотезам проводится с применением специальных критериев, из которых наиболее часто используется предложенный К. Пирсоном критерий c². При использовании данного критерия необходимо, чтобы объем вариационного ряда и частоты интервалов были достаточно велики (m_i > 5, n > 50). В случае необходимости соединяют два соседних интервалов или более.

Формула критерия 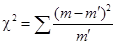[xciii], где m — эмпирические частоты; 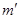— теоретические частоты.

По соответствующей таблице (Таблица вероятностей R (c²) для критерия c^2[xciv]) находится при заданном числе степеней вероятность достижения c² данного значения, т.е. R (c²). При вероятностях, значительно отличающихся от нуля, расхождение между теоретическими и эмпирическими частотами считается случайным.

Данный критерий используется в следующих типовых ситуациях.

Ситуация 1. Проверка гипотезы о соответствии эмпирического распределения данных некоторому теоретическому закону распределения, например нормальному закону распределения.

Пример П1.15. Среднесписочная численность работников на предприятии (𝑚) составляет 350 человек. По уровню заработной платы численность сотрудников разбита на 7 групп. Необходимо было пересмотреть ставки заработной платы. Для определения частот лиц, получающих ту или иную заработную плату, были определены теоретические частоты 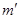. Было найдено расчетное значение c² = 5,2, которое при числе степеней свободы равно 4 (поскольку 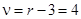). c² зависит от числа связей, их 3 (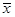, s, 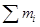). По таблице[xcv] при a = 0,05 и n = 4 c²_табл = 9,49. Поскольку c²_факт < c²_табл, т.е. 5,2 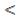9,49, то с вероятностью 0,95 заключаем, что расхождения между теоретическими и эмпирическими частотами случайны и изменения заработной платы будут проходить в тех же группах по численности сотрудников без долевых изменений.

Ситуация 2. Проверка гипотезы о согласии эмпирического распределения с любым распределением — равномерным, распределением Пуассона (число степеней свободы 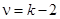) или другими известными. Если c²_факт < c²_табл, то гипотеза о распределении случайной величины по закону Пуассона не отклоняется, если же c²_факт > c² _табл., то гипотеза отклоняется.

Ситуация 3. Анализ таблиц сопряженности двух переменных для установления факта наличия и уровня значимости взаимосвязи (если нулевая гипотеза об отсутствии связи отклоняется, т.е. c²_факт > c² _табл, то необходимо измерить тесноту связи).

Изучение взаимосвязи между качественными признаками проводится в различных экономических и социологических исследованиях, где информация собирается при помощи опросов или анкетирования. На основе собранного материала строятся комбинационные таблицы, простейшей формой которых являются таблицы взаимной сопряженности — четырехпольные (четырехклеточные) таблицы. В таких таблицах по каждому признаку выделяют только две группы, чаще всего по альтернативному принципу «да»/«нет». Вывод о зависимости признаков можно получить при помощи критерия c² Пирсона. Для получения выводов о наличии или отсутствии взаимосвязи между двумя альтернативными признаками рассчитываются теоретические частоты (частости), а затем проводится сопоставление эмпирических и теоретических частот по одной из формул: 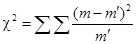или 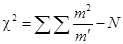[xcvi], где N — общая численность единиц совокупности. Рассчитав c²_факт, сравнивают его с c²_табл по табл. П2.10. Число степеней свободы подсчитывается по формуле 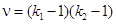, где k ₁ и k ₂ — число групп по первому и второму признакам. Если c²_факт > c²_табл, то выдвинутая нулевая гипотеза о случайном распределении отвергается, т.е. существует зависимость между факторами.

Если теоретические и эмпирические частоты совпадают, это свидетельствует о независимости признаков, т.е. нулевая гипотеза принимается.

Пример П1.16. В результате опроса сотрудников учреждения о зависимости отношения к работе и уровня образования были получены данные, которые затем были оформлены в таблице «четырех полей» (табл. П1.9).[xcvii]

Таблица П1.9

Данные для примера П1.16

Уровень образования	Отношение к работе	Итого
Недовольны работой	Довольны работой
Среднее общее	92 (a)	43 (b)
Высшее	18 (c)	237 (d)
Итого

Решение

Для расчета теоретических частот следует в первую очередь определить долю (процент) лиц, недовольных предоставленной работой: d = 110/390 = 0,28 (28%); процент лиц, которых удовлетворяет работа, будет соответственно равен 72. Поэтому проводим пересчет эмпирических частот с учетом рассчитанных долей по группам.

В первой строке теоретические частоты: 0,28×135 = 37,8» 38 человек, 0,72×135 = 97,2» 97 человек. Для второй строки имеем 0,28×255 = 71,4» 71 человек и 0,72×255 = 183,6» 184 человека.

Подставим в формулу:

.

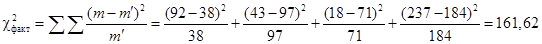Определяем c²_табл при числе степеней свободы 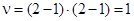и уровне значимости a = 0,05: c²_табл = 3,84. Поскольку c²_факт > c²_табл, распределение считается неслучайным, нулевая гипотеза отвергается и можно утверждать, что отношение к предоставленной работе зависит от уровня образования.

Пример П1.17. Было проведено обследование числа телезрителей (мужчин и женщин), просмотревших телевизионный сериал. Мнение телезрителей представлено в табл. П1.10.[xcviii]

Таблица П1.10

Данные для примера П1.17

Отношение к постановке	Пол	Итого
мужчины	женщины
Положительное
Безразличное
Отрицательное
Итого

Решение

Число степеней свободы .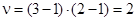

Расчет теоретических частот по первому столбцу (мужчинам): ; ; .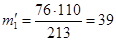

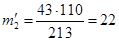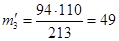Расчет теоретических частот по второму столбцу (женщинам): ; ; .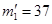

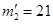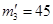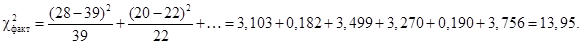
При числе степеней свободы n = 2, a = 0,05 c²_табл = 5,99.

Таким образом, нулевая гипотеза не принимается, а это значит, что между факторами существует связь и распределение неслучайно.

Ситуация 4. Коэффициенты взаимной сопряженности К. Пирсона, А. Чупрова, Г. Крамера основаны на критерии c², они принимают значение от 0 до 1; равенству нулю означает отсутствие связи между изучаемыми признаками, если же имеем равенство единице, то это означает полную связь. Коэффициенты взаимной сопряженности симметричные меры связи[xcix] и могут быть использованы для измерения тесноты связи лишь после того, как факт наличия связи будет доказан на основе критерия c².

Ситуация 5. Коэффициент конкордации (множественный коэффициент ранговой корреляции) характеризует связь между несколькими признаками, измеренными по порядковой шкале. Он рассчитывается по формуле 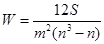, где 𝑚 — число ранжируемых признаков; S — сумма квадратов отклонений суммы 𝑚 рангов от их средней величины; 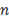— число ранжируемых единиц (число наблюдений). Формула для W несколько видоизменяется, если существуют связанные ранги.

Значимость коэффициента конкордации проверяется на основе критерия c², рассчитываемого по формуле 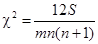. Полученное значение (c²_факт) сравнивается с табличным c²_табл. Число степеней свободы определяется по формуле 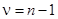. Допустим, имеем c²_табл = 14,07; при 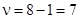и при a = 0,05, c²_факт = 19,87, т.е. c²_табл. 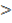c²_факт[c]_. В этом случае можно предположить, что полученное значение коэффициента конкордации статистически значимо.

Коэффициент конкордации используется при экспертных оценках, когда необходимо определить степень согласованности мнения у экспертов по тому или другому вопросу.

Пример П1.18. На соревнованиях по спортивным танцам четверо судей оценивают в баллах выполнение программы спортсменами. Оцениваютсяспортсмены по трем признакам: синхронность выполнения программы парами, трудность программы, чистота выполнения прыжков (табл. П1.11). [ci]

Таблица П1.11

Данные для примера П1.18

№ судей	Ранги по каждому фактору	R	R 2	R – T	(R – T)2
Синхронное выполнение	Трудность программы	Чистота выполнения прыжков
						–3,5	12,25
						–1,5	2,25
						1,5	2,25
						3,5	12,25
Итого						—	29,00

Решение

Величина T определяется как 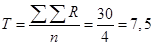;[cii] 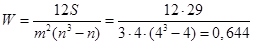. Коэффициент конкордации изменяется от 0 до 1, поэтому рассчитанный коэффициент характеризует среднюю зависимость между мнениями судей. Проверим данный коэффициент на существенность, т.е. значимость. Подставим данные в формулу: 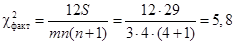. При a = 0,05 и числе степеней свободы 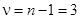табличное значение c²_табл = 7,81. Поскольку c²_факт < c²_табл, это свидетельствует о несущественности коэффициента конкордации. Иначе говоря, мнение судей о представленных программах спортсменами неоднозначно.

На практике используются критерии[ciii], основанные на критерии c² Пирсона. Это критерии согласия В.И. Романовского и Б.С. Ястремского.

Критерий согласия Романовского 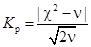, число степеней свободы определяется, как и при соответствии нормальному распределению, по формуле 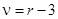, где r — число групп, 3 — число связей (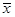, s, n). Он удобен для расчетов при отсутствии таблиц для c². Если 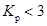, то расхождение между теоретическим и эмпирическим распределением считаются случайны, если же 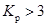, то расхождения считаются неслучайными, т.е. распределение не отвечает требованиям нормального распределения.

Критерий Ястремского, в отличие от всех критериев согласия, которые указывали лишь вероятную оценку расхождения между эмпирическим и теоретическим распределениями, дает прямой ответ на вопрос о мере расхождения. Его формула 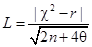[civ], где r — количество групп, θ — величина, зависящая от количества групп, но при количестве групп, меньшем 20, принимается равной 0,6. Величина L распределена нормально, поэтому с вероятностью 0,997 она по абсолютной величине не должна превышать трех. Поэтому при L £ 3 эмпирическое распределение соответствует теоретическому закону распределения, если же L > 3, эмпирическое распределение не укладывается в рамки теоретического распределения.

Пример П1.19. На основе данных примера П1.15 сделаем расчет величин 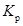и L.

Решение

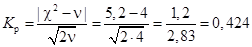. Поскольку 0,424 < 3, то можно утверждать что расхождения между теоретическими и эмпирическими частотами случайны, т.е. нулевая гипотеза не отвергается.

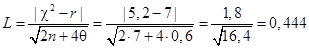. Поскольку[cv] 0,444 < 3, расхождение между эмпирическими и теоретическим частотами считается случайным, т.е. нулевая гипотеза не отвергается.

11. Таблица П2.11. Значения функции P (l).

Основное условие применения критерия Колмогорова[cvi] — это достаточно большая совокупность. Применение этого критерия основано на накопительных частотах или частостях — фактических и теоретических.

Определяется тестовая статистика — величина 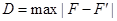, где F и 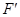— эмпирические и теоретические частоты. Далее по формуле определяется величина l для критерия Колмогорова, 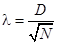. Затем по таблице определяется вероятность, с которой можно утверждать, что отклонения эмпирических данных от теоретических случайны. Вероятность P (l) находится в пределах от 0 до 1.

Если l принимает значения до 0,3, то считается, что P (l) = 1 и имеет место полное совпадение частот.

Пример П1.20. Имеем совокупность единиц, равную 80, которая разбита на 5 групп. Определяются теоретические частоты, сумма которых равна 78. Затем проводится накопление частот по эмпирическому и теоретическому рядам. По каждой группе находится разность между фактическими и теоретическими частотами и выделяется максимальная разность D по модулю. Допустим, D _max = 5,0, по формуле 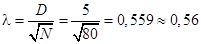. По табл. П2.11 находим значения вероятности, с которой можно утверждать, что отклонения эмпирических частот от теоретических случайны либо нет. Вероятность P (l) может изменяться от 0 до 1. В нашем случае значение вероятности P (l) равно P (0,56) = 0,9111, что свидетельствует о высоком уровне случайности расхождения между эмпирическими и теоретическими частотами.

Задача П1.8. В табл. П1.12 приведены данные о производстве металлических изделий определенного веса.

Таблица П1.12

Данные для задачи П1.8