 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Характеристики погрешностей измерений известны
|
|
a) Измерения однократные. Постановка задачи полиномиальной аппроксимации некоторой исследуемой функции y = f (x)и метод ее решения изложены в разд. 2.3.7.1, 2.3.7.2. В соответствии с материалами этих разделов исходными данными для полиномиальной аппроксимации функции y = f (x)являются ее значения в k дискретных точках, возмущенные погрешностями. Эти значения были объединены в вектор 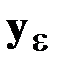 . С другой стороны, вектор точных значений аппроксимируемой функции выражался, как
. С другой стороны, вектор точных значений аппроксимируемой функции выражался, как 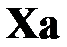 , где
, где 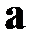 – вектор точных значений коэффициентов искомого полинома. Степень искомого полинома q полагалась известной, а погрешности – распределенными нормально:
– вектор точных значений коэффициентов искомого полинома. Степень искомого полинома q полагалась известной, а погрешности – распределенными нормально: 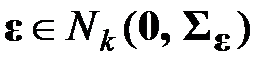 . Тогда вектор отсчетов также распределен нормально:
. Тогда вектор отсчетов также распределен нормально: 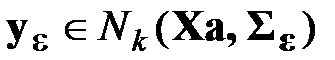 , то есть
, то есть 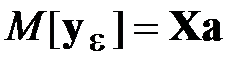 . Эта ситуация именовалась как случай известной модели.
. Эта ситуация именовалась как случай известной модели.
В разд. 2.3.7.2 были получены ММП-оценки 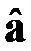 коэффициентов путем минимизации квадратичных форм
коэффициентов путем минимизации квадратичных форм
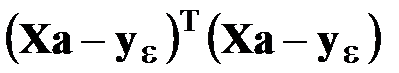 – для равноточных измерений и применения МНК;
– для равноточных измерений и применения МНК;
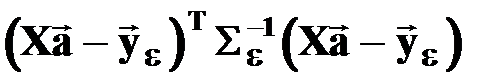 – для неравноточных измерений и применения ОМНК.
– для неравноточных измерений и применения ОМНК.
Из-за случайности погрешностей измерений оценки 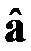 также случайны, а значит, случайными являются векторы
также случайны, а значит, случайными являются векторы 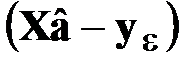 и вслед за ними – квадратичные формы, которые определены в разд. 2.3.7.2:
и вслед за ними – квадратичные формы, которые определены в разд. 2.3.7.2:
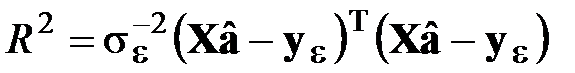 – при применении МНК;
– при применении МНК;
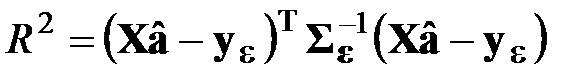 – при применении ОМНК.
– при применении ОМНК.
Поскольку найденные оценки коэффициентов несмещены,
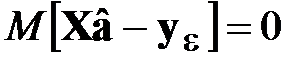 .
.
В разд. 2.3.7.3 приведены плотности распределения этих квадратичных форм в условиях, когда плотности распределения погрешностей нормальны и модель известна. Плотности распределения обеих квадратичных форм одинаковы: это плотность распределения хи-квадрат с k – q – 1 степенями свободы, то есть
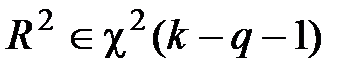 .
.
На практике модель практически никогда не бывает известной. Тогда при ошибочном назначении степени p аппроксимирующего полинома, меньшей, чем истинная степень q, оценки коэффициентов оказываются смещенными (см. также п. 2.3.7.4, замечание 4), поэтому 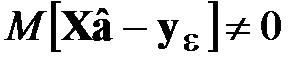 , значения
, значения 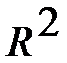 существенно возрастают, и плотность распределения изменяется. При увеличении степени аппроксимирующего полинома и в особенности при p > q ухудшается обусловленность матриц
существенно возрастают, и плотность распределения изменяется. При увеличении степени аппроксимирующего полинома и в особенности при p > q ухудшается обусловленность матриц 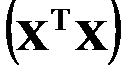 и
и 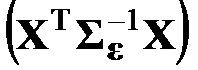 , и теряется вычислительная устойчивость МНК и ОМНК (см. разд. 2.3.7.7). Поэтому случаи, когда p > q, не рассматриваются.
, и теряется вычислительная устойчивость МНК и ОМНК (см. разд. 2.3.7.7). Поэтому случаи, когда p > q, не рассматриваются.
Итак, пусть в изложенных условиях при истинной степени аппроксимирующего полинома q была назначена степень p < q, и с помощью МНК или ОМНК получены оценки p + 1 коэффициента. Обозначим вектор найденных таким образом оценок 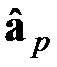 , а квадратичные формы, вычисленные при этих значениях оценок –
, а квадратичные формы, вычисленные при этих значениях оценок – 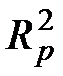 .
.
Сформулируем гипотезу.
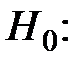 степень аппроксимирующего полинома p = q;
степень аппроксимирующего полинома p = q;
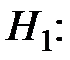 степень аппроксимирующего полинома p < q.
степень аппроксимирующего полинома p < q.
Статистикой критерия проверки этой гипотезы является величина 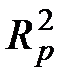 , которая при p = q, то есть при справедливости нулевой гипотезы, равна
, которая при p = q, то есть при справедливости нулевой гипотезы, равна 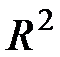 и распределена как
и распределена как 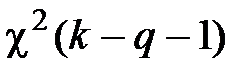 (см. разд. 2.3.7.3). Поэтому в качестве критического значения при заданной вероятности a выбирается (1 - a)100-процентная квантиль из таблицы квантилей распределения хи-квадрат с (k - q - 1) степенями свободы.
(см. разд. 2.3.7.3). Поэтому в качестве критического значения при заданной вероятности a выбирается (1 - a)100-процентная квантиль из таблицы квантилей распределения хи-квадрат с (k - q - 1) степенями свободы.
П р о ц е д у р а п р о в е р к и г и п о т е з ы в условиях, когда заданы вид полинома (степенной, обобщенный по разд. 2.3.7.9) и вероятность a.
1. Оценивают коэффициенты полинома
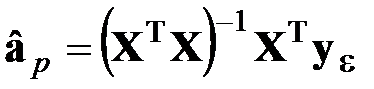 или
или 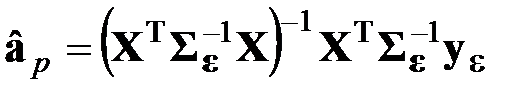 .
.
2. Вычисляют статистику критерия
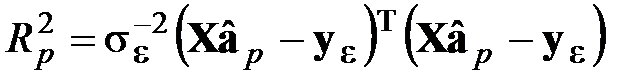
или 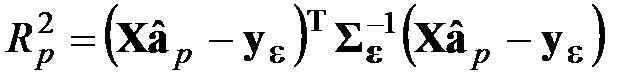 .
.
3. Значение статистики 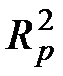 сравнивают с критическим значением:
сравнивают с критическим значением:
если 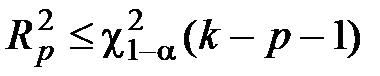 , делают вывод о том, что нет достаточных оснований для того, чтобы отвергнуть нулевую гипотезу;
, делают вывод о том, что нет достаточных оснований для того, чтобы отвергнуть нулевую гипотезу;
в противном случае, если 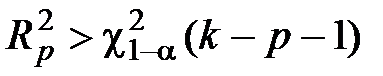 , делают вывод о том, что нет достаточных оснований для того, чтобы считать нулевую гипотезу справедливой.
, делают вывод о том, что нет достаточных оснований для того, чтобы считать нулевую гипотезу справедливой.
b) Измерения многократные.
Этот случай отличается от предыдущего тем, что в качестве исходных данных для полиномиальной аппроксимации используется не вектор результатов однократных измерений 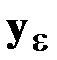 , а вектор средних арифметических значений
, а вектор средних арифметических значений 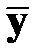 результатов многократных измерений. В условиях, перечисленных ранее для однократных измерений, вектор средних арифметических значений обладает свойствами (см. также разд. 2.3.4.3, 2.3.7.5):
результатов многократных измерений. В условиях, перечисленных ранее для однократных измерений, вектор средних арифметических значений обладает свойствами (см. также разд. 2.3.4.3, 2.3.7.5):
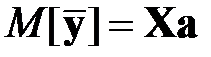 ,
, 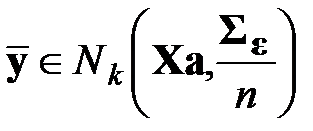 ,
, 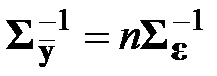 .
.
При равноточных измерениях, когда применяется МНК,
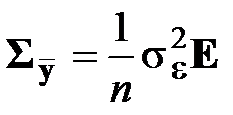
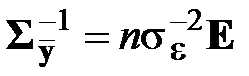 ,
,
где E – единичная матрица (см. также разд. 2.3.7.2).
Если для аппроксимации назначена степень полинома p и 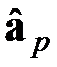 - вектор оценок (p + 1) коэффициента этого полинома, то статистикой критерия проверки гипотезы о степени полинома будет
- вектор оценок (p + 1) коэффициента этого полинома, то статистикой критерия проверки гипотезы о степени полинома будет
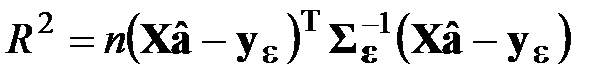 .
.
Когда измерения равноточные и применяется МНК,
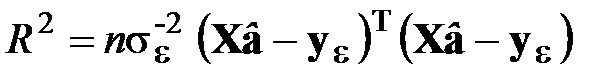 .
.
Как и ранее, при условии справедливости нулевой гипотезы, то есть при p = q, 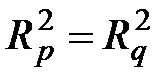 и
и 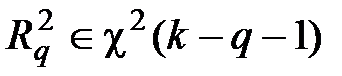 Критическое значение при заданном значении вероятности a есть
Критическое значение при заданном значении вероятности a есть 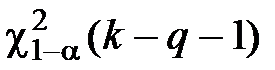 .
.
Гипотеза формулируется по аналогии с формулировкой, приведенной для однократных измерений.
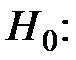 степень аппроксимирующего полинома p = q,
степень аппроксимирующего полинома p = q,
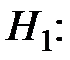 степень аппроксимирующего полинома p < q.
степень аппроксимирующего полинома p < q.
П р о ц е д у р а п р о в е р к и г и п о т е з ы в условиях, когда заданы вид полинома (степенной, обобщенный по разд. 2.3.7.9) и вероятность a.
1. Оценивают коэффициенты полинома
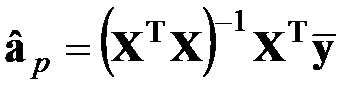 или
или 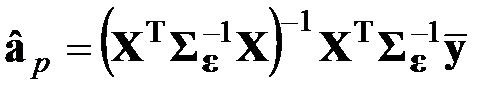 .
.
2. Вычисляют статистику критерия
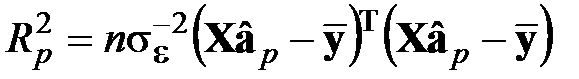 или
или 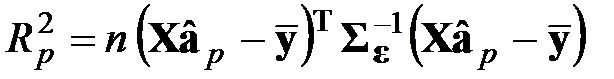 .
.
3. Значение статистики 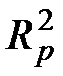 сравнивают с критическим значением:
сравнивают с критическим значением:
если 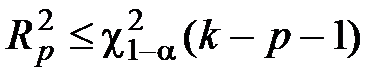 , делают вывод о том, что нет достаточных оснований для того, чтобы отвергнуть нулевую гипотезу;
, делают вывод о том, что нет достаточных оснований для того, чтобы отвергнуть нулевую гипотезу;
в противном случае, если 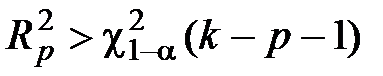 , делают вывод о том, что нет достаточных оснований для того, чтобы считать нулевую гипотезу справедливой.
, делают вывод о том, что нет достаточных оснований для того, чтобы считать нулевую гипотезу справедливой.
Заметим, что в соответствии с центральной предельной теоремой плотность распределения средних арифметических асимптотически нормальна. Поэтому, начиная с n = 15–20, требования к нормальности погрешностей измерений могут быть значительно смягчены.
2.5.6.3. Проверка гипотезы о степени аппроксимирующего полинома,
характеристики погрешностей измерений неизвестны
Если характеристики погрешностей измерения значений аппроксимируемой функции неизвестны, то неизбежно приходится выполнять многократные измерения и по результатам этих измерений оценивать характеристики погрешностей: дисперсии 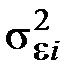 или ковариационную матрицу
или ковариационную матрицу 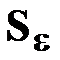 . Выполнение эксперимента в этой ситуации и вычисление оценок производится в соответствии с указаниями разд. 2.3.4.3, 2.3.4.4, 2.3.7.6. Для выяснения равноточности или неравноточности выполненных измерений проверяется гипотеза о равенстве дисперсий по критерию Кочрена (см. разд. 2.5.6.1) и принимается решение о применении МНК или ОМНК. При вынужденном пренебрежении коррелированностью между измерениями по причинам, отмеченным в разд. 2.3.4.7, матрица
. Выполнение эксперимента в этой ситуации и вычисление оценок производится в соответствии с указаниями разд. 2.3.4.3, 2.3.4.4, 2.3.7.6. Для выяснения равноточности или неравноточности выполненных измерений проверяется гипотеза о равенстве дисперсий по критерию Кочрена (см. разд. 2.5.6.1) и принимается решение о применении МНК или ОМНК. При вынужденном пренебрежении коррелированностью между измерениями по причинам, отмеченным в разд. 2.3.4.7, матрица 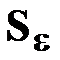 оказывается диагональной (см. разд. 2.3.7.6), и это обстоятельство несколько снижает эффективность оценок коэффициентов аппроксимирующего полинома, но оценки коэффициентов остаются несмещенными, если, конечно, назначенная степень полинома p равна истинной степени q.
оказывается диагональной (см. разд. 2.3.7.6), и это обстоятельство несколько снижает эффективность оценок коэффициентов аппроксимирующего полинома, но оценки коэффициентов остаются несмещенными, если, конечно, назначенная степень полинома p равна истинной степени q.
Здесь, как и ранее в разд. 2.5.6.2, “б”), в качестве исходных данных для полиномиальной аппроксимации используется не вектор результатов однократных измерений 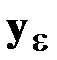 , а вектор средних арифметических значений
, а вектор средних арифметических значений 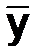 результатов многократных измерений. С учетом замены матрицы
результатов многократных измерений. С учетом замены матрицы 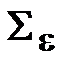 ее оценкой
ее оценкой 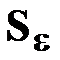 (см. разд. 2.5.6.2, б)
(см. разд. 2.5.6.2, б)
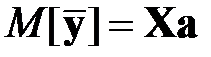 ,
, 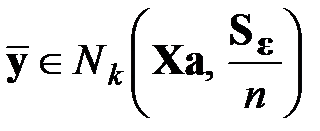 ,
, 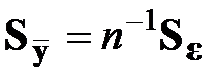 .
.
Если по результатам проверки гипотезы о равенстве дисперсий по критерию Кочрена принято решение о применении МНК, то
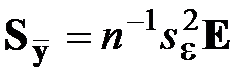 ,
, 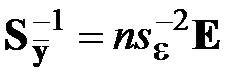 ,
,
где E – единичная матрица, 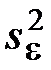 – оценка дисперсии равноточных измерений, которая вычисляется, как среднее арифметическое значение оценок дисперсий
– оценка дисперсии равноточных измерений, которая вычисляется, как среднее арифметическое значение оценок дисперсий 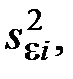 найденных при каждом значении
найденных при каждом значении 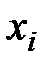 , как указано в разд. 2.3.7.6:
, как указано в разд. 2.3.7.6:
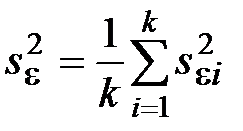 .
.
Если для аппроксимации назначена степень полинома p, и 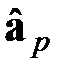 – вектор оценок p - 1 коэффициента этого полинома, и по результатам проверки гипотезы о равенстве дисперсий принято решение о применении МНК, статистикой критерия проверки гипотезы о степени полинома будет
– вектор оценок p - 1 коэффициента этого полинома, и по результатам проверки гипотезы о равенстве дисперсий принято решение о применении МНК, статистикой критерия проверки гипотезы о степени полинома будет
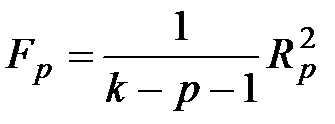 ,
,
где 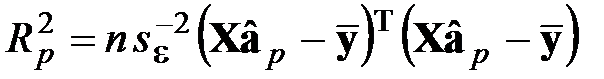 ;
;
в противном случае, при применении ОМНК,
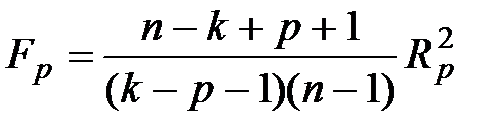 ,
,
где 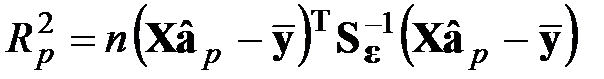 .
.
При условии справедливости нулевой гипотезы, то есть при p = q, как указано выше в разд. 2.3.7.6, статистика 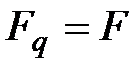 в обоих случаях распределена по закону распределения Фишера (см. [5], стр. 485):
в обоих случаях распределена по закону распределения Фишера (см. [5], стр. 485):
при применении МНК 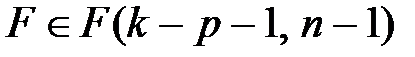 с количеством степеней свободы (k - p - 1) и (n - 1);
с количеством степеней свободы (k - p - 1) и (n - 1);
при применении ОМНК 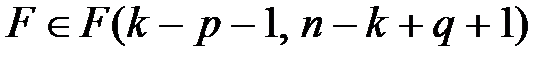 с количеством степеней свободы (k - p - 1) и (n - k + p + 1).
с количеством степеней свободы (k - p - 1) и (n - k + p + 1).
Гипотеза о степени полинома формулируется по аналогии с формулировкой, приведенной в разд. 2.5.6.2:
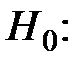 степень аппроксимирующего полинома p = q,
степень аппроксимирующего полинома p = q,
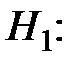 степень аппроксимирующего полинома p < q.
степень аппроксимирующего полинома p < q.
П р о ц е д у р а п р о в е р к и г и п о т е з ы в условиях, когда заданы вид полинома (степенной, обобщенный по разд. 2.3.7.9) и вероятность a,а также вычислены оценки 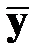 и
и 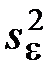 или
или 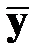 и
и 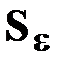 .
.
1. Оценивают коэффициенты полинома
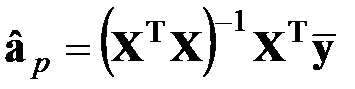 или
или 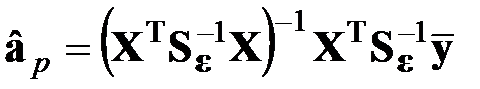 .
.
2. Вычисляют статистику критерия
в случае МНК 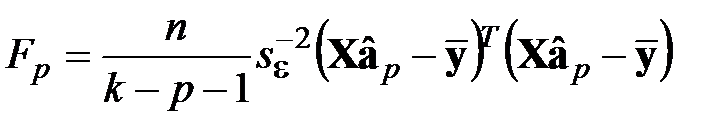 ;
;
в случае ОМНК 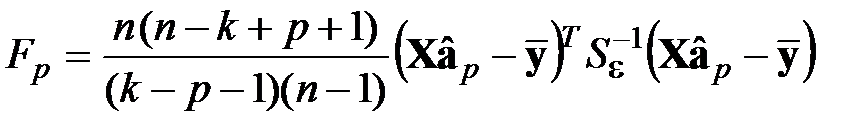 .
.
3. Значение статистики 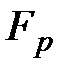 сравнивают с критическим значением распределения Фишера:
сравнивают с критическим значением распределения Фишера:
при МНК, если 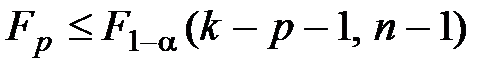 ;
;
при ОМНК, если 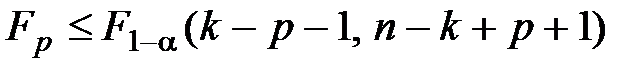 ;
;
делают вывод о том, что нет достаточных оснований для того, чтобы отвергнуть нулевую гипотезу;
в противном случае делают вывод о том, что нет достаточных оснований для того, чтобы считать нулевую гипотезу справедливой.
Критические значения плотности распределения Фишера приведены в таблицах математической статистики (см. [13, 14] и др.)
Дата публикования: 2014-10-20; Прочитано: 465 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
