Функции распределения и плотности распределения

Рассмотрим двумерный случайный вектор, то есть двумерный вектор, каждая составляющая которого есть непрерывная случайная величина:

.

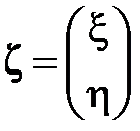Как и ранее, случайный вектор и его случайные компоненты обозначим греческими буквами, а значения, которые может принимать вектор и его компоненты – соответствующими латинскими буквами, то есть будем считать, что случайный вектор ζ принимает значения

.

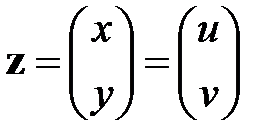Функция распределения двумерного случайного вектора есть вероятность совместного осуществления событий:

.

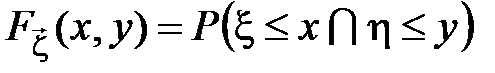Плотность распределения, как и ранее, есть производная от функции распределения по обоим аргументам:

,

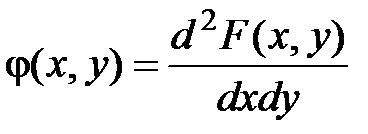поэтому

.

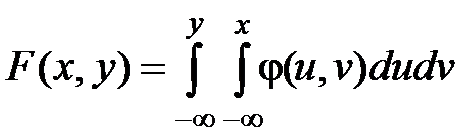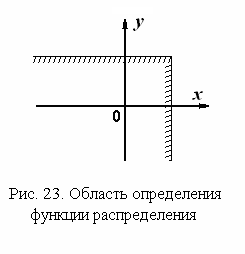
Область интегрирования показана на рис. 23.

В силу монотонности вероятностной меры функция распределения – неубывающая функция по каждому аргументу, поэтому плотность распределения есть неотрицательная функция двух аргументов, которая описывает некоторую поверхность над координатной плоскостью. Эта поверхность приближается к плоскости x0y при удалении значений аргументов от начала координат в любом направлении. Понятно, что

.

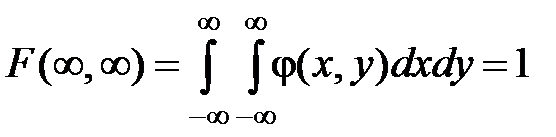Если по одному из аргументов ограничений нет, то

.

.

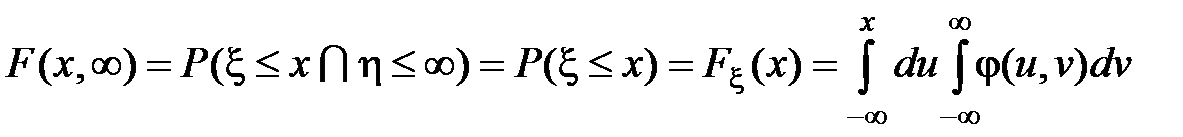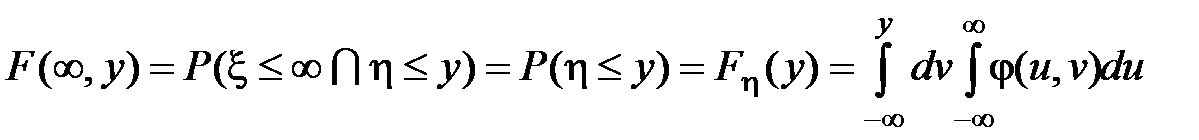Таким образом мы получили маргинальные (частные) функции распределения 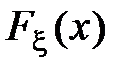и 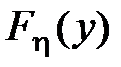. Дифференцирование этих функций по их аргументам, то есть дифференцирование соответствующих интегралов по их верхним пределам, по определению, дает маргинальные (частные) плотности распределения:

, .

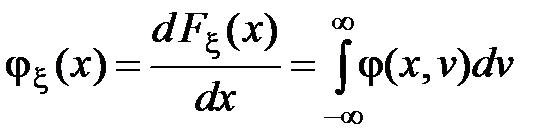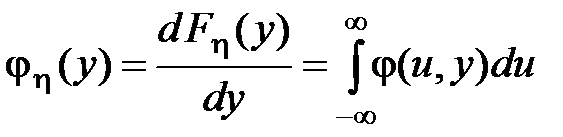Определим условную функцию распределения, то есть функцию распределения одной из случайных величин при условии, что другая случайная величина принимает некоторое конкретное значение, например,

.

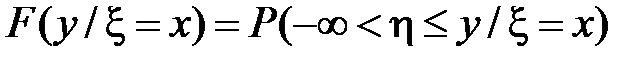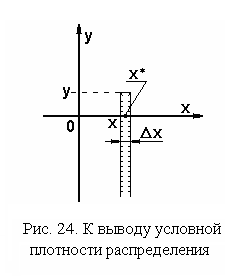
Выделим на координатной плоскости область, показанную на рис. 24.

Вероятность того, что случайный вектор принимает значения из этой области, равна 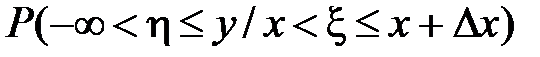. В соответствии с формулой для условной вероятности из разд. 1.2.3

.

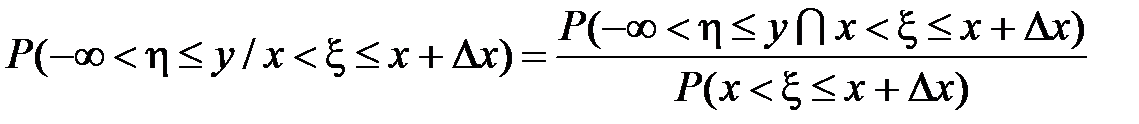Условная функция распределения получается в результате предельного перехода:

.

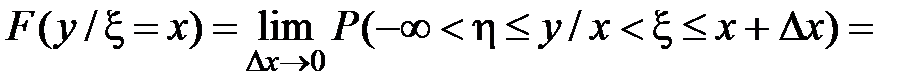
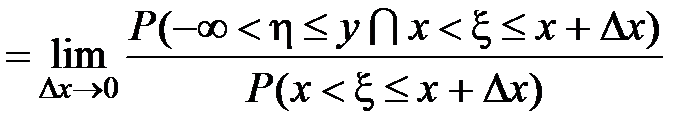
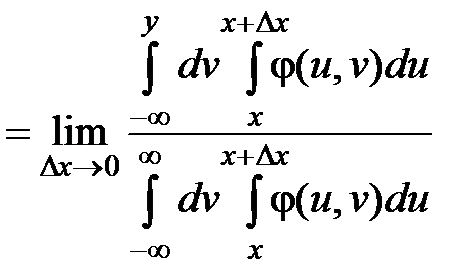По теореме о среднем, внутри интервала 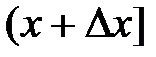найдется точка 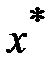, такая, что

,

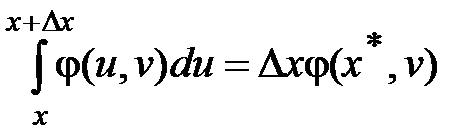поэтому

.

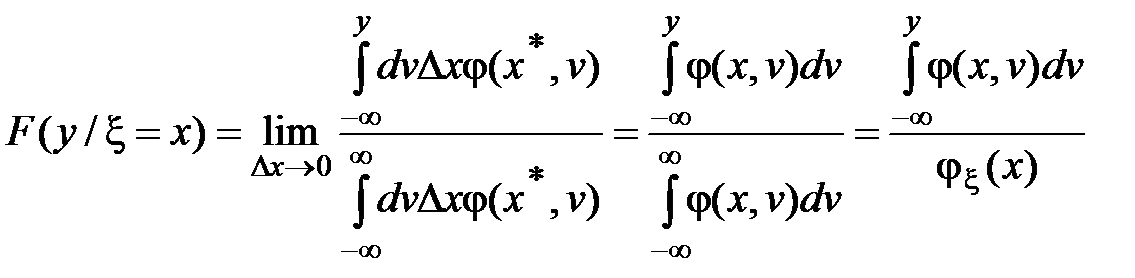Условная плотность распределения есть производная от условной функции распределения:

.

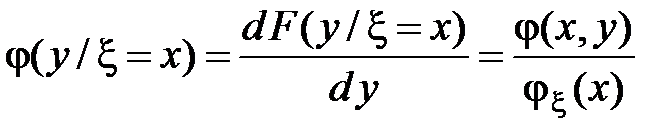Аналогично

.

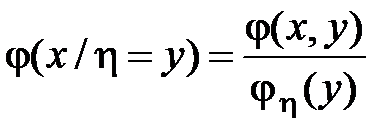Обычно обозначают 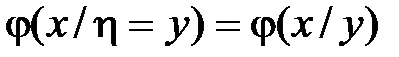и 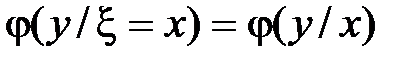. В этих обозначениях из полученных формул следует

, .

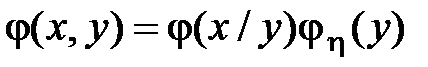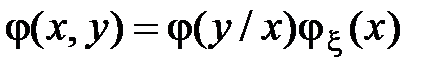С учетом этих соотношений перепишем формулы для маргинальных распределений в виде:

, .

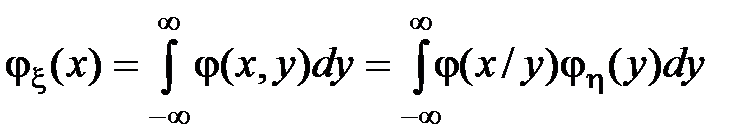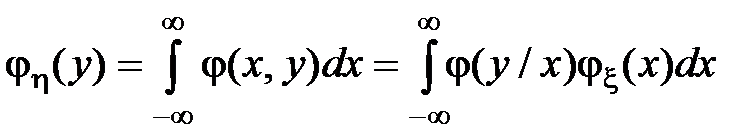Это формулы полной вероятности для непрерывных случайных величин.

Поскольку 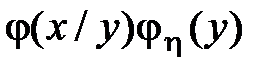= 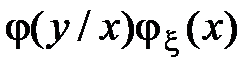, получаем формулу Байеса для непрерывных случайных величин:

.

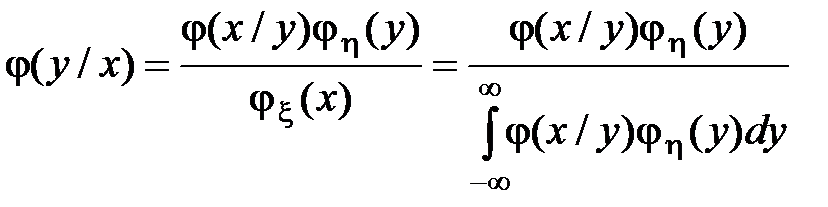Если x и h независимы, то 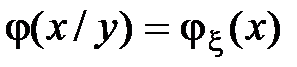, 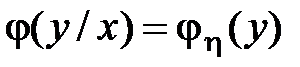и поэтому .

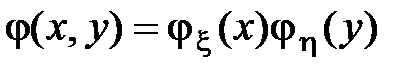Справедливо и обратное: если 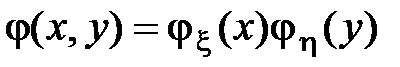, то из этого с необходимостью следует независимость x и h.

Признак независимости случайных величин: две случайные величины независимы тогда и только тогда, когда их совместная плотность распределения может быть представлена как произведение маргинальных плотностей распределения этих величин (см. также разд. 1.2.3).