 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятия генеральной и выборочной дисперсий и формулы вычисления
|
|
В качестве характеристики разброса значений количественного признака X вокруг своего среднего значения используется дисперсия.
Определение. Генеральной дисперсией 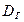 называют средне арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения
называют средне арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения 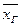 .
.
Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются числовой характеристикой, называемой средним квадратическим отклонением.
Определение. Генеральным средним квадратическим отклонениемназывают корень квадратный из генеральной дисперсии и обозначают в виде
Пусть для изучения генеральной совокупности относительно количественного признака 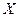 произведена выборка объема
произведена выборка объема 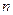 .
.
Определение. Выборочной дисперсией 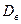 называется среднее арифметическое квадратов отклонений наблюдаемых значений выборки от выборочной средней
называется среднее арифметическое квадратов отклонений наблюдаемых значений выборки от выборочной средней 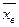 .
.
Если все значения признака 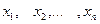 выборки объема
выборки объема 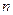 различны, то
различны, то
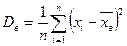 .
.
Если же значения признака 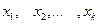 имеют соответственно частоты
имеют соответственно частоты 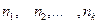 , причем
, причем 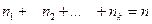 , то
, то
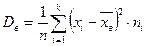 .
.
Определение. Выборочным средним квадратическим отклонениемназывают корень квадратный из выборочной дисперсии и обозначают в виде
 .
.
Записанные выше формулы вычисления выборочной и генеральной дисперсии можно упрости, используя следующую теорему.
Теорема. Дисперсия равна разности между средним квадратов значений признака и квадратом общей средней, то есть
 , где
, где 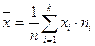 и
и 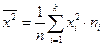 .
.
Пример. Выборочная совокупность задана таблицей распределения
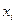
| ||||
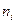
|
Найти выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение.
Решение.
Найдем выборочную среднюю.
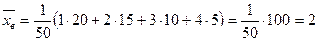 .
.
Найти выборочную дисперсию.
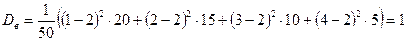 .
.
Общая средняя уже известна 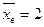 .
.
Найдем среднюю квадратов значений признака:
 .
.
Тогда 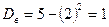 и
и 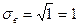 - это среднее отклонение от среднего значения выборки, то есть от числа
- это среднее отклонение от среднего значения выборки, то есть от числа 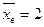 .
.
Если в качестве оценки генеральной дисперсии использовать выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещенной оценкой генеральной дисперсии, т.е. 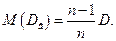
Несмещенной оценкой генеральной дисперсии является исправленная выборочная дисперсия

Обе предложенные оценки - выборочная дисперсия и исправленная выборочная дисперсия – являются состоятельными оценками генеральной дисперсии, и разница между ними заметна лишь при небольшом числе наблюдений n. При n > 30 в качестве оценки для D вполне можно использовать Dв. В случае нормально распределенной генеральной совокупности обе эти оценки также являются асимптотически эффективными, т.е. при n →∞ они будут стремиться к эффективной оценке.
Для оценки же среднего квадратического отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно корню квадратному из исправленной дисперсии и обозначается в виде
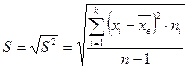 .
.
Пример. Найти выборочную и исправленную дисперсии для следующего статистического распределения
| |||||
|
Решение.
Найдем выборочную среднюю.
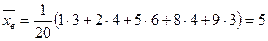 .
.
Найдем выборочную дисперсию по определению.
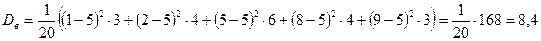 .
.
Тогда 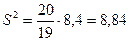 .
.
Дата публикования: 2014-10-20; Прочитано: 13036 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
