Біртекті сызықты жүйелер

2.1. Төмендегідей біртекті сызықты теңдеулер жүйесін қарастырайық:

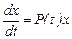(1)

Осы жүйенің шешімдерінің кейбір қасиеттерін келтірейік. Ең алдымен ескеретін жәй – біртекті жүйенің бастапқы Коши есебінің 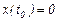шартын қанағаттандыратын нөлдік 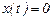шешімі барлық уақытта бар және ол шешім жалғыз.

Теорема-1. Егер 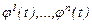– вектор-функциялары (1) жүйенің шешімдері болса, олардың кез келген сызықты комбинациясы да сол жүйенің шешімі болады.

Дәлелдеуі. Берілген функциялардың нақты сандар өрісіндегі сызықты комбинациясын алайық:

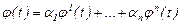(2)

Мұндағы, әрбір 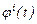функциясы үшін

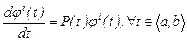
тепе-теңдігі орындалады.

Осыдан,

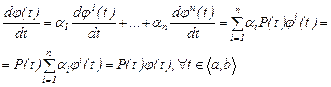
Теорема-2. Егер (1) жүйенің комплексты 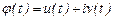шешімі бар болса, онда оның нақты және жорамал бөліктері өз алдарына (1) жүйенің шешімін береді.

Дәлелдеуі. Шарт бойынша

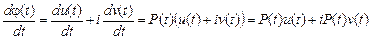
Осыдан,

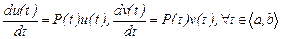(3)

Анықтама-1. Егер 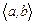аралығында анықталған 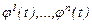функциялары үшін бәрі бірдей нөлге тең емес 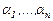сандары табылып,

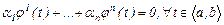(4)

теңдігі орындалса, онда берілген функциялар жиыны 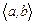аралығында сызықты тәуелді деп аталынады, ал (4) теңдік 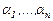сандарының тек нөлдік мәндерінде ғана орындалса, онда берілген функциялар жиыны 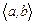аралығында сызықты тәуелсіз деп аталады.

Ескерту. Егер берілген функциялар жиыны 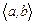аралығында сызықты тәуелді болса, онда сол аралыққа жататын кез келген 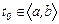нүктесінде де тәуелді болады. Кері ұйғарым орындалмайды, өйткені бұл жағдайда 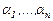сандары 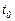-ға тәуелді болады. Ал егер берілген функциялар жиыны белгілі бір дифференциалдық теңдеулер жүйесінің шешімдері болса, онда бір нүктедегі тәуелділік пен тәуелсіздік сәйкес аралықтағы тәуелділік пен тәуелсіздікке эквивалент.

Анықтама-2. Біртекті сызықты жүйенің 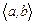аралығында анықталған сызықты тәуелсіз шешімдер жиынын сол жүйенің осы аралықтағы базисі немесе фундаменталь шешімдер жүйесі деп атайды.

2.2. Айталық, 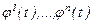вектор-функциялары (1) жүйенің шешімдері болсын. Әрбір бағанасы осы векторлардың координаттарынан тұратын төмендегідей матрица құрайық:

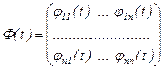(5)

Осы матрицаның анықтауышын Вронский анықтауышы немесе вронскиан деп атайды және оны 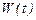- деп белгілейді. Сонымен,

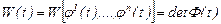(6)

Егер (5) матрицаның анықтауышы нөлге тең болмаса, онда ол матрица фундаменталь матрица деп аталынады.

Теорема-3. Егер 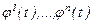функциялары 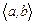аралығында сызықты тәуелді болса, онда осы аралықта олардың вронскианы нөлге тең болады.

Дәлелдеуі. Анықтама бойынша

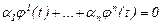(7)

мұнда 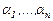сандарының бәрі бірдей нөл емес. Соңғы қатынасты координаттар бойынша ашып жазсақ, төмендегідей біртекті сызықты жүйе аламыз:

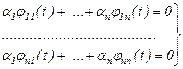(8)

Бұл жүйенің нөлдік емес шешімі бар болу үшін оның анықтауышы нөлге тең болуы шарт, яғни .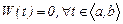

Теорема-4. Егер 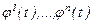функциялары (1) жүйенің 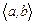аралығындағы сызықты тәуелсіз шешімдері болса, онда осы аралықтың кез келген нүктесінде вронскиан нөлге тең болмайды.

Дәлелдеуі. Кері жориық. Айталық, кейбір 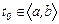нүктеде 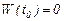болсын. Белгісіз 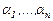сандары арқылы төмендегідей теңдік құрайық:

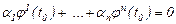(9)

немесе координаттары бойынша:

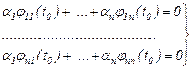(10)

Бұл жүйенің анықтауышы нөлге тең, өйткені ол анықтауыш 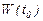. Сондықтан, оның нөлдік емес шешімі бар: .

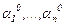Берілген шешімдердің сызықты комбинациясын қарастырайық:

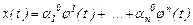(11)

Бұл вектор-функция берілген жүйенің шешімі болады (теорема-1).

Осындағы 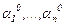сандары (9) теңдікті қанағаттандырғандықтан, 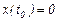теңдігі орындалады, яғни (11) шешімнің бастапқы мәні нөлге тең. Шешімнің жалғыздық шарты бойынша 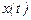нөлдік шешім. Сондықтан,

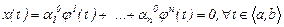(12)

Соңғы тепе-теңдік 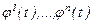векторларының сызықты тәуелділігін көрсетеді. Бұл - теореманың шартына қайшы.

Соңғы екі теореманы біріктіріп айтсақ, мынандай қорытындыға келеміз: (1) жүйенің шешімі 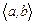аралығында сызықты тәуелсіз болу үшін олардың вронскианының 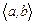аралығының бірде-бір нүктесінде нөлге тең болмауы қажетті және жеткілікті.

Теорема-5. Егер 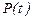матрицасы 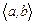аралығында үздіксіз болса, онда (1) жүйенің базисы әрқашанда бар болады және егер 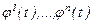жүйенің базисы болса, онда оның жалпы шешімі мына түрде жазылады:

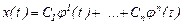(13)

мұндағы, 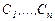- кез келген тұрақты сандар.

Дәлелдеуі. Кез келген сызықты тәуелсіз векторлар: 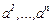үшін кейбір 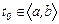нүктесінде

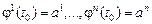(14)

шартын қанағаттандыратын шешімдер жиынын алсақ, жеткілікті. Бастапқы 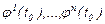мәндері сызықты тәуелсіз болғандықтан, бұл шешімдер 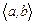аралығында да тәуелсіз, яғни олар (1) жүйенің базисын құрайды.

Енді (13) қатынастың жалпы шешім болатынын көрсетейік. Біріншіден, бұл қатынас шешімдердің сызықты комбинациясы болғандықтан, 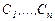сандарының барлық мәндерінде жүйенің шешімі болады (теорема-1). Екіншіден, одан кез келген Коши есебінің шешімін алуға болады. Ол үшін

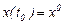(15)

шартын қоялық, яғни

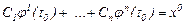(16)

Бұл векторлық теңдікті координаттары бойынша ашып жазсақ,

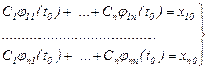(17)

жүйесін аламыз. Оның анықтауышы нөлге тең емес. Сондықтан, (17) жүйенің тек жалғыз ғана шешімі бар: 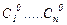. Осы тұрақтыларды (13) қатынасқа қойсақ, (15) шартты қанағаттандыратын дербес шешім аламыз.

2.3. Жалпы шешімді фундаменталь матрица арқылы жазуға болады. Айталық, 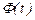берілген (1) жүйенің фундаменталь матрицасы болсын. Оның әрбір бағанасы тәуелсіз векторлардың координаттары болғандықтан, бұл матрица матрицалық

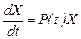(18)

теңдеудің шешімі болады, яғни

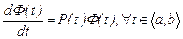(19)

Осы матрицаны пайдалансақ, жалпы шешім

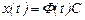(20)

түрінде жазылады. Мұнда 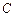- кез келген тұрақты вектор. Бұл қатынастан Коши есебінің шешімін анықтауға болады: (15) бастапқы шартты пайдалансақ,

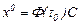
теңдігін аламыз. Осыдан 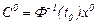. Сонда

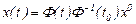(21)

түріндегі дербес шешім аламыз. Егер 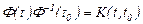белгілеуін енгізсек, соңғы теңдік былай жазылады:

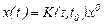(22)

Осындағы 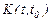матрицасын Коши матрицасы деп атайды.

Егер соңғы қатынастағы 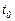-ді тұрақталған сан, ал 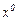-ді тұрақталмаған вектор деп есептесек, онда (22) қатынасты жүйенің Коши түріндегі жалпы шешімі деп атайды.

Егер кейбір 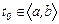нүктесінде 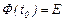теңдігі орындалса, онда 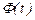матрицасы 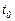нүктесінде қалыпталған (нормаланған) деп аталады. Бұл жағдайда шешім

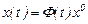(23)

түрінде жазылады.

Теорема-6. Егер 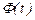фундаменталь матрица болса, онда 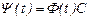матрицасы да фундаменталь матрица болады. Мұнда 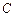- тұрақты 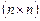- өлшемді ерекше емес матрица.

Шынында да,

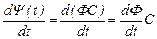
Ал 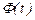матрицасы (18) матрицалық теңдеуді қанағаттандыратындықтан,

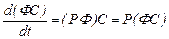
тепе-теңдігін аламыз, яғни 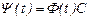матрицасы да (18) матрицалық теңдеуді қанағаттандырады. Оның үстіне

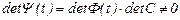
2.4. Лиувилль формуласын келтірейік.

Алдымен, -ші ретті анықтауыштың туындысы қалай ашылатынын көрсетейік.

-ші ретті анықтауыштың туындысы сол анықтауыштың әр бағанасы (немесе әр жатық жолы) кезекпен туындыларымен ауыстырылған анықтауыштардың қосындысынан тұрады. Осы ереже бойынша вронскианның туындысын ашайық:

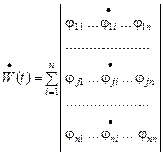(24)

Мұндағы, 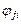берілген жүйенің шешімі болғандықтан,

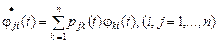
Осы өрнектерді анықтауыштың 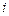-нші бағанасына қойсақ, анықтауыштың қасиеттері бойынша, 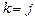болатын қосындыдан басқа анықтауыштардың бәрі нөлге тең болады, өйткені олардың екі бағанасы өзара пропорционал болады. Сондықтан,

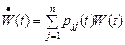
Осыдан

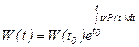(25)

Мұндағы, 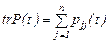- берілген 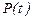матрицасының ізі деп аталады.

Осы (25) теңдікті Лиувилль формуласы деп атайды. Бұл формуладан мынандай қорытынды шығады: егер 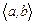аралығының бір нүктесінде вронскиан нөлге тең болса, ол бүкіл аралықта нөлге тең болады, ал 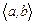аралығының бір нүктесінде нөлге тең болмаса, онда ол бүкіл аралықта нөлге тең болмайды.

2.5. Айталық, 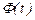- фундаменталь матрица болсын.

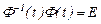тепе-теңдігін дифференциалдайық:

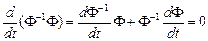
Осыдан

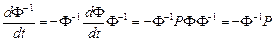
немесе

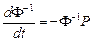
Соңғы қатынастағы матрицаларды аударсақ,

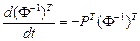
теңдігін аламыз. Бұдан шығатын қорытынды, 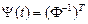матрицасы

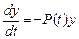(27)

теңдеуінің фундаменталь матрицасы болатынын көреміз. Осы (27) жүйені берілген (1) жүйенің түйіндесі деп атайды. Егер 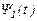осы жүйенің кейбір фундаменталь матрицасы болса, онда

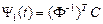
қатынасы орын алады. Мұнда 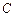-ерекше емес матрица. Осыдан

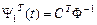
немесе

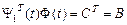
Соңғы теңдіктен мынаны көреміз: 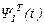- матрицасының жатық жолы (27) жүйенің шешімдері болатынын, 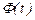матрицасының бағаналары (1) жүйенің шешімдері болатыны, ал олардың көбейтіндісі тұрақты екенін көреміз.