Ысқаша мазмұны. Тұрақты коэффициентті сызықты теңдеулерді интегралдау

Тұрақты коэффициентті сызықты теңдеулерді интегралдау

6.1. Алдымен біртекті теңдеуді қарастырайық:

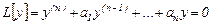(1)

Мұндағы, 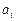- тұрақты нақты сандар.

Бұл теңдеудің шешімін Эйлер ұсынған әдіс бойынша

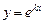(2)

түрінде іздейміз. Мұндағы, 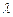- белгісіз тұрақты сан. Осы өрнекті (1) теңдеудің сол жағына қойсақ,

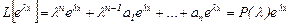(3)

қатынасын аламыз. Мұнда

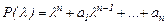(4)

(3) қатынастан 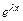функциясы теңдеудің шешімі болу үшін 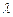санының 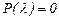теңдеуінің шешімі болуы керек екенін көреміз, яғни

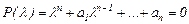(5)

Соңғы теңдеуді сипаттаушы теңдеу деп, ал оның түбірлерін сипаттаушы сандар деп атайды.

Сипаттаушы сандардың түрлеріне байланысты фундаменталь шешімдер жүйесі әртүрлі болады. Сол жағдайларды қарастырайық.

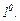Сипаттаушы 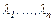сандары әртүрлі нақты сандар болсын.

Бұл сандарды кезекпен (2) қатынасқа қойып, дербес шешім табамыз:

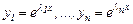(6)

Олардың сызықты тәуелсіздігін көрсету үшін Вронский анықтауышын құрайық:

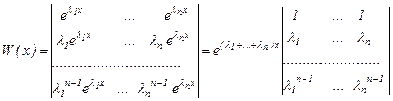
Соңғы анықтауыш Вандермонд анықтауышы деп аталады. Ол 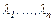сандары әртүрлі болғанда нөлге айналмайды, яғни 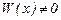. Сондықтан, (6) функциялар жиыны берілген теңдеудің фундаменталь шешімдер жүйесін құрайы. Бұл жағдайда жалпы шешім

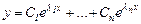(7)

түрінде жазылады. Мұндағы, 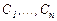- еркін тұрақты сандар.

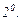Сипаттаушы сандардың ішінде комплексты сандар кездессін. Айталық, 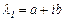- сипаттаушы теңдеудің жәй түбірі болсын. Онда оның түйіндесі 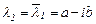саны да сол теңдеудің түбірі болады. Бұл жағдайда 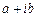түбіріне сәйкес шешім

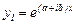(8)

түрінде жазылады. Бұл комплексты функция. Өткен параграфта көрсетілген сызықты теңдеудің шешімдерінің қасиеті бойынша оның нақты және жорамал бөліктері өз алдына берілген теңдеудің шешімдері болады. Сондықтан,

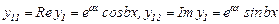(9)

функциялары (1) теңдеудің шешімдері болады және олар өзара сызықты тәуелсіз. Ал 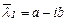түбіріне сәйкес шешім де сол өзара тәуелсіз екі функцияны береді:

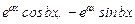(10)

Бұлардың біріншісі, алдыңғымен бірдей; екіншісі, тек таңбасымен өзгеше, яғни (9) және (10) функциялар өзара сызықты тәуелді. Сондықтан, өзара түйіндес комплекс түбір үшін (9) түріндегі екі нақты функция алынады. Осы сияқты, кез келген қос комплексты түбір үшін екі нақты функциялар алынып отырады. Оларға қоса нақты түбірлерге сәйкес қойылатын шешімдерді алсақ, олардың жиыны берілген теңдеудің фундаменталь шешімдер жүйесін құрайды.

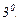Сипаттаушы теңдеудің түбірлерінің кейбіреулері еселікті түбірлер болсын.

Айталық, 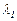-саны сипаттаушы теңдеудің 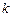-еселікті түбірі болсын. Бұл жағдайда

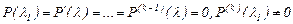(11)

шарттары орындалады.

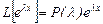
тепе-теңдігін 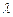бойынша 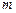рет дифференциалдайық:

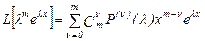(12)

Осыдан (11) шартты ескерсек:

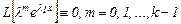
болатынын көреміз, яғни

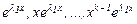(13)

функцияларының (1) теңдеудің шешімдері болатынын көреміз. Бұл шешімдердің де өзара сызықты тәуелсіз екенін көрсету қиын емес. Мұнда, 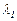-саны нақты болса, онда (13) функциялар да нақты функциялар болады.

Егер сипаттаушы теңдеудің комплексты 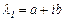түбірі 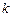еселікті түбір болса, оның түйіндесі 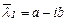түбірі де 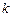еселікті болады. Бұл жағдайда да алдыңғы (13) шешімдер сияқты төмендегідей 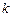шешім аламыз:

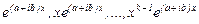(14)

Осы комплексты функциялардың нақты және жорамал бөліктерін ажыратсақ, онда 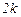нақты функциялардың жиынын аламыз:

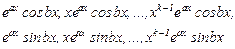(15)

Бұл функциялардың да сызықты тәуелсіздігін дәлелдеу қиын емес. Түйіндес 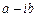түбірі жаңа тәуелсіз шешімдер тудырмайды.

Сонымен, әрбір нақты, комплексты, еселікті түбірлерге сәйкес қойылатын шешімдерді есептесек, барлығы нақты шешімдер аламыз. Олардың сызықты комбинациясы берілген теңдеудің жалпы шешімін береді.