Ысқаша мазмұны. 3.1. Жоғарғы ретті теңдеулердің ең қарапайымы және оңай зерттелетіні – сызықты теңдеулер

3.1. Жоғарғы ретті теңдеулердің ең қарапайымы және оңай зерттелетіні – сызықты теңдеулер.

Белгісіз функция мен оның туындыларын сызықты түрде байланыстыратын теңдеулерді сызықты теңдеулер деп татйды.

- ретті сызықты теңдеудің жалпы түрі былай жазылады:

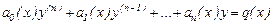
Мұндағы, 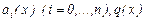- функциялары кейбір 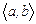аралығында анықталған нақты үздіксіз функциялар.

Егер 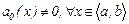болса, онда соған бөлу арқылы

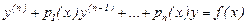(1)

теңдеуін аламыз. Соңғы түрдегі теңдеуді теңдеудің келтірілген, не қалыпты түрі деп атайды. Мұндағы, 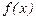функциясы бос мүше деп аталынады. Егер ол нөлге тең болмаса, (1) теңдеу біртексіз сызықты теңдеу деп, ал нөлге тең болса, біртекті сызықты теңдеу деп аталынады. (1) теңдеудің сәйкес біртектісі былай жазылады:

(2)

Әдетте, (1) теңдеудің сол жағын қысқартып, былай белгілейді:

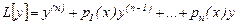(3)

Сонда (1) және (2) теңдеулерді былай жазуға болады:

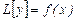
және

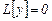
Енгізілген (3) өрнекті сызықты дифференциалдық оператор деп атайды. Бұл оператор дифференциалдау амалының сызықтығынан шығатын төмендегідей екі шартты қанағаттандырады:

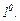
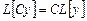
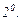
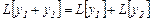
Бұлардың салдары ретінде тағы бір қатынасты жазуға болады:

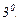
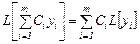
Бұл шарттар дифференциалдық оператордың сызықтығын білдіреді.

3.2. Сызықты теңдеулердің ортақ екі қасиетін келтірейік.

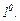Тәуелсіз айнымалыны кейбір 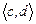аралығында анықталған рет үздіксіз дифференциалданатын, бірінші туындысы нөлге тең емес функция арқылы жаңа тәуелсіз айнымалымен алмастырғаннан теңдеудің сызықтығы өзгермейді.

Шынында да, 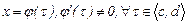алмастыруын жасайық. Сонда

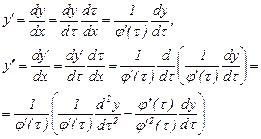
Осылай кез келген 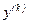-ның сызықты түрде 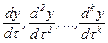арқылы өрнектелетінін көреміз. Осы қатынастарды (1) және (2) теңдеулерге апарып қойсақ, қайтадан сызықты теңдеулер аламыз.

2⁰. Белгісіз функцияны басқа бір функциямен сызықты түрде алмастырғаннан теңдеудің сызықтығы өзгермейді.

Шынында да, айталық, 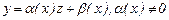түрінде алмастыру жасалсын. Мұндағы, 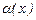және 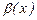функциялары 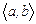аралығында анықталған рет үздіксіз дифференциалданатын функциялар болсын.

Сонда

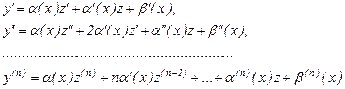
Осы туындыларды (1) теңдеуге апарып қойсақ, қайтадан біртексіз сызықты теңдеу аламыз.

Ал (2) теңдеуге апарып қойсақ, онда біртекті теңдеуіміз біртексіз сызықты теңдеуге айналады. Біртектілікті сақтау үшін 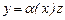түріндегі біртекті алмастыру алу керек.

Сызықты теңдеулердің бір ерекшелігі – олардың бастапқы шартты қанағаттандыратын шешімі бар болу үшін бір-ақ шарттың орындалуы жеткілікті.

Дәлірек айтсақ, мынандай тұжырым орын алады.

Теорема-1. Егер сызықты теңдеудің коэффициенттері мен бос мүшесі кейбір 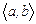аралығында анықталған үздіксіз функциялар болса, онда оның бастапқы шартты қанағаттандыратын жалғыз ғана шешімі болады және ол шешім 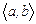аралығының өн бойында анықталады.

Бұл тұжырымды дәлелдеу қиындық туғызбайды.