Вторая теорема двойственности

Тесная связь между двумя взаимно двойственными задачами проявляется не только в равенстве оптимальных значений их линейных функций, о чем утверждалось в первой (основной) теореме двойственности.

Пусть даны две взаимно двойственные задачи I - (6.1)-(6.3) и II - (6.4)-(6.6). Если каждую из этих задач решать симплексным методом, то необходимо их привести к каноническому виду, для чего в систему ограничений (6.2) задачи I (в краткой записи ) следует ввести m неотрицательных переменных ,а всистему ограничений (6.5) задачи II () n неотрицательных переменных ,где i (j) — номер неравенства, в которое введена дополнительная переменная .

Системы ограничений каждой из взаимно двойственных задач примут вид:

. (6.12)

. (6.13)

Установим следующее соответствие между первоначальными переменными одной из двойственных задач и дополнительными переменными другой задачи:

Переменные исходной задачи I
Первоначальные	Дополнительные
Дополнительные	Первоначальные
Переменные исходной задачи II

Теорема 6.1. Положительным (ненулевым) компонентам оптимального решения одной из взаимно двойственных задач соответствуют нулевые компоненты оптимального решения другой задачи, т.е. для любых i = 1, 2,..., т и у = 1, 2,..., п:

если , то ; если , то 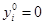и аналогично,

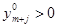если , то ; если , то .

Из теоремы вытекает важный вывод о том, что введенное ранее соответствие (6.14) между переменными взаимно двойственных задач при достижении оптимума (т.е. на последнем шаге решения каждой задачи симплексным методом) представляет соответствие между основными (как правило, не равными нулю) переменными одной из двойственных задач и неосновными (равными нулю) переменными другой задачи, когда они образуют допустимые базисные решения.

Рассмотренная теорема является следствием следующей теоремы.

Вторая теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные ее оптимального решения.

Пример 6.5. Убедиться в справедливости второй теоремы двойственности для взаимно двойственных задач I и II, приведенных в примере 6.2.

Решение. На основании выражения (6.14) установим следующее соответствие между переменными. В гл. 5 обе задачи были решены симплексным методом. На последнем шаге решения каждой задачи (см. с. 54 и с. 57) получено:

в исходной задаче I в двойственной задаче II

(6.20) (6.21)

при при

оптимальном базисном оптимальном базисном

решении решении

Компоненты оптимального решения двойственной задачи

равны (по абсолютной величине) коэффициентам при соответствующих переменных линейной функции (6.20), которую можно представить в виде а компоненты оптимального решения исходной задачи равны коэффициентам при соответствующих переменных линейной функции (6.21), которую можно представить в виде .

Замечание. Если в одной из взаимно двойственных задач нарушается единственность оптимального решения, то оптимальное решение двойственной задачи вырожденное. Это связано с тем, что при нарушении единственности оптимального решения исходной задачи в выражении линейной функции ее оптимального решения через неосновные переменные отсутствует хотя бы одна из неосновных переменных.

С помощью теорем двойственности можно, решив симплексным методом исходную задачу, найти оптимум и оптимальное решение двойственной задачи.

Пример 6.6. Решить симплексным методом задачу

при ограничениях

.

и найти оптимум и оптимальное решение двойственной задачи, используя теоремы двойственности.

Решение. Решая задачу симплексным методом, получим на последнем шаге решения (рекомендуем читателю убедиться в самостоятельно): , т.е при оптимальном базисном решении = (4;7;0;0;6;6).

В данной задаче соответствие (6.14) между переменными примет вид:

На основании первой теоремы двойственности . На основании второй теоремы двойственности оптимальное решение двойственной задачи = (2/7; 3/7; 0; 0; 0; 0), так как , т.е. коэффициенту при соответствующей переменной х ₃в выражении линейной функции F (x), 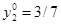, т.е. коэффициенту при переменной из-за отсутствия соответствующих переменных х ₅, х ₆, x ₁, х ₂в выражении F (x)их коэффициенты равны нулю. Итак, в двойственной задаче Z _min = 10 при = (2/7; 3/7; 0; 0; 0; 0).

Метод, при котором вначале симплексным методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находятся с помощью теорем двойственности, называется двойственным симплексным методом. Этот метод бывает выгодно применять, когда первое базисное решение исходной задачи недопустимое или, например, когда число ее ограничений m больше числа переменных n.