Linear Programming Output summary 15 страница

7. В модели примера 5.5.1 обозначим через x_tj объем перевозок между пунктами i и у. Задачу этого примера можно сформулировать как задачу линейного программирования, у которой каждому пункту транспортной сети соответст­вует ограничение в виде равенства. Сформулируйте задачу ЛП и покажите, что в ограничениях коэффициенты а_1} при переменных x_tj определяются сле­дующим образом.

238 Глава 5. Транспортные модели

1, для ограничения /, а ■ = < - I, для ограничения j, О, в противном случае.

8. Агентство по трудоустройству имеет заявки на рабочих на следующие пять месяцев.

Месяц 1 2 3 4 5

К-во рабочих 100 120 80 170 50

Стоимость рабочей силы зависит от длительности периода трудоустройства (см. следующую таблицу).

Длительность периода трудоустройства (месяцы) 1 2 3 4 5

Стоимость трудоустройства одного рабочего (долл.) 100 130 180 220 250

Сформулируйте задачу линейного программирования. Затем путем алгеб­раических преобразований ограничений покажите, что эту задачу можно свести к транспортной. Найдите ее оптимальное решение. (Совет. Для пре­образования общей задачи ЛП в транспортную используйте представление коэффициентов ограничений из предыдущего упражнения.)

ЛИТЕРАТУРА

1. BazaraaM., Jarvis J., SheraliM. Linear Programming and Network Flows, 2nd ed., Wiley, New York, 1990.

2. Dantzig G. Linear Programming and Extensions, Princeton University Press, Prin­ceton, N. J., 1963. (Русский перевод: Данциг Дж. Линейное программирование, его применение и обобщение. — М.: Прогресс, 1966.)

3. Murty К. Network Programming, Prentice Hall, Upper Saddle River, N. J., 1992.

Литература, добавленная при переводе

1. Ашманов С. А. Линейное программирование. — М.: Наука, 1981.

2. Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования транспорт­ного типа. — М.: Наука, 1969.

КОМПЛЕКСНЫЕ ЗАДАЧИ

5.1. ⁹ Компания ABC Cola имеет завод по производству безалкогольных напит­ков в северной части островного государства Таванда. Напитки выпускают­ся в трех различных упаковках: возвращаемых стеклянных бутылках, алюминиевых консервных банках и невозвращаемых пластмассовых бу­тылках. Стеклянные бутылки складируют и затем возвращают на завод для повторного использования.

Задача построена на материалах статьи Cheng Т., Chlu С. "A Case Study of Production Expan­sion Planning in a Soft-Drink Manufacturing Company", Omega, Vol. 16, No. 6, pp. 521-532,1988.

Комплексные задачи 239

Поскольку спрос на безалкогольные напитки постоянно растет, компания ABC Cola планирует построить еще один завод в центральной или южной час­ти острова. Прогнозируемый спрос на безалкогольные напитки (выраженный в количестве упаковок) на следующие пять лет показан в табл. 5.46.

Таблица 5.46

			Года
Вид упаковки
Возвращаемая стеклянная
Банки
Невозвращаемая пластмассовая

Плановые возможности существующего завода по выпуску продукции по­казаны в табл. 5.47.

Таблица 5.47

			Года
Вид упаковки
Возвращаемая стеклянная
Банки
Невозвращаемая пластмассовая

Компания имеет 6 складов для стеклотары: N1 и N2 расположены в се­верной части острова, С1 и С2 — в центральной части, S1 и S2 — в юж­ной. Доля стеклотары, обрабатываемой каждым складом, показана в табл. 5.48.

Таблица 5.48

Склад Доля (в процентах)

N1 85

N2 15

С1 60

С2 40

51 80

52 20

Из общего количества стеклотары примерно 60% приходится на северные склады, 15% — на центральные и 25% — на южные.

Компания планирует построить новый завод по производству безалкогольных напитков либо в центре, либо на юге острова. Транспортные расходы, рассчи­танные на одну упаковку напитка в стеклянных бутылках, приведены в табл. 5.49. Транспортные расходы на напитки в банках и пластмассовых бу­тылках составляют соответственно 60 и 70% от аналогичных расходов на транспортировку напитков в стеклянных бутылках.

Определите, где целесообразнее построить новый завод: в центральном рай­оне или на юге острова?

240 Глава 5. Транспортные модели

Таблица 5.49

Транспортные расходы на одну упаковку (долл.)

Склад	Существующий завод	Завод в центральном районе	Завод в южном районе
N1	0,80	1,30	1,90
N2	1,20	1,90	2,90
С1	1,50	1,05	1,20
С2	1,60	0,80	1,60
S1	1,90	1,50	0,90
S2	2,10	1,70	0,80

5.2. В ходе строительства международного аэропорта в г. Брисбен для укреп­ления болотистого грунта необходимо произвести песчаную насыпь общим объемом 1 355 000 м³ на девяти площадках аэропорта. Песок берется из расположенных вблизи аэропорта пяти небольших карьеров. Некоторые строительные подразделения, обслуживающие стройплощадки, выделены для прокладки дорог внутри аэропорта и по его периметру. Для насыпи пе­сок берется со стройплощадок. Расстояние (в сотнях метров) от карьеров до стройплощадок показано в табл. 5.50, где также приведены потребности в песке стройплощадок и возможности карьеров (в 100 м³).

Таблица 5.50

										Возможн карьер
								8,5
					1,5
						ОО
						оо
Потребности

стройплощадок _

a) Управление строительством оценивает объем перемещения песка [объем (м³) х расстояние (100 м)] в 2 495 000 соответствующих единиц при стоимости 0,65 долл. за единицу. Достаточно ли приведенного объе­ма песка для выполнения запланированных работ?

b) Управление строительством пришло к выводу, что подвоз песка к некото­рым стройплощадкам не возможен до завершения строительства дороги во­круг аэропорта (длиной 900 м). В табл. 5.51 значком "х" обозначены стройплощадки, к которым не возможен подвоз песка (из определенных карьеров) до завершения строительства окружной дороги. Как организо­вать подвоз песка с учетом этого ограничения?

Задача построена на материалах статьи Perry С, Ilief М. "Earth Moving on Construction Projects", Interfaces, Vol. 13, No. 1, pp. 79-84, 1983.

Комплексные задачи

Таблица 5.51

1 2 3 4 5

5.3. Десять лет назад некий предприниматель организовал доставку оптовых фармацевтических товаров с центрального склада (ЦС) на автофургонах. С тех пор значительно увеличился спрос на фармацевтическую продукцию и появились два новых товарных склада (С1 и С2). Центральный склад, традиционно имеющий больший ассортимент товаров, время от времени выручал новые склады в обеспечении кратковременных заказов. Такая взаимовыручка со временем привела к тому, что треть своих заказов новые склады выполняли за счет товаров, полученных с центрального склада. В табл. 5.52 приведено количество заказов, выполняемых тремя товарными складами для шести потребителей, обозначенных П1-П6.

Таблица 5.52

Маршрут

Откуда

Куда

Количество заказов

ЦС	С1
ЦС	С2
ЦС	П1
ЦС	П2
ЦС	ПЗ
С1	П1
С1	ПЗ
С1	П4
С1	П5
С2	П2
С2	П5
С2	П6

Предприниматель постоянно совершенствовал способы доставки заказов, придерживаясь принципа децентрализации, когда каждому товарному складу была определена своя зона доставки товара, покрывающая всех по­требителей, получающих заказы с этого склада. Но управляющие складами комплектовали заказы согласно своим "сферам влияния". Например, менед­жеры центрального склада гордились тем, что поставляют товары не только обычным потребителям, но и другим товарным складам. Поэтому зачастую разные склады поставляют заказы одному и тому же потребителю.

В табл. 5.53 приведены расстояния (в милях) между складами и потребите­лями. В автофургон обычно помещается 100 товарных заказов.

Оцените организацию перевозок предпринимателя и предложите свой план перевозок.

242 Глава 5. Транспортные модели

Таблица 5.53

	ЦС	С1	С2	П1	П2	ПЗ	П4	П5	П6
цс
С1
С2
П1
П2
ПЗ
П4
П5
П6

5.4. Авиакомпания KeeWee выполняет полеты между городами А и В согласно расписанию, приведенному в табл. 5.54. Экипаж может вернуться в свой го­род не ранее чем через 90 минут после прилета либо на следующий день. Со­ставьте расписание назначения экипажей на рейсы, минимизирующее сум­марное время простоев всех экипажей.

Таблица 5.54

Рейс Отлет из города А Прилет в город В Рейс Отлет из города В Прилет в город А

А1	6:00	8:30	В1	7:30	9:30
А2	8:15	10:45	В2	9:15	11:15
A3	13:30	16:00	ВЗ	16:30	18:30
А4	15:00	17:30	В4	20:00	22:00

ГЛАВА 6

СЕТЕВЫЕ МОДЕЛИ

В рамках теории исследования операций рассматривается большое количество практических задач, которые можно сформулировать и решить как сетевые моде­ли. Недавние исследования показывают, что не менее 70% реальных задач матема­тического программирования можно представить в виде сетевых моделей. Приве­дем несколько конкретных примеров.

1. Проектирование газопровода, соединяющего буровые скважины морского базирования с находящейся на берегу приемной станцией. Целевая функция соответствующей модели должна минимизировать стоимость строительства газопровода.

2. Поиск кратчайшего маршрута между двумя городами по существующей сети дорог.

3. Определение максимальной пропускной способности трубопровода для транспортировки угольной пульпы от угольных шахт к электростанциям.

4. Определение схемы транспортировки нефти от пунктов нефтедобычи к неф­теперерабатывающим заводам с минимальной стоимостью транспортировки.

5. Составление временного графика строительных работ (определение дат нача­ла и завершения отдельных этапов работ).

Решение приведенных задач (как и многих аналогичных) требует применения различных сетевых оптимизационных алгоритмов. В этой главе будут рассмотрены следующие пять алгоритмов.

1. Алгоритм нахождения минимального остовного дерева (пример 1).

2. Алгоритм поиска кратчайшего пути (пример 2).

3. Алгоритм определения максимального потока (пример 3).

4. Алгоритм минимизации стоимости потока в сети с ограниченной пропускной способностью (пример 4).

5. Алгоритм определения критического пути (пример 5).

Задачи, вытекающие из перечисленных примеров, можно сформулировать и решать как задачи линейного программирования. Однако специфическая струк­тура этих задач позволяет разработать специальные сетевые алгоритмы, более эф­фективные, чем стандартный симплекс-метод.

Глава 6. Сетевые модели

6.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Сеть состоит из множества узлов, связанных дугами (или ребрами).¹ Таким образом, сеть описывается парой множеств (N, А), где ТУ — множество узлов, а А— множество ребер. Например, сеть, показанная на рис. 6.1, описывается следующим образом.

#={1,2,3,4, 5},

А= {(1, 2), (1, 3), (2, 3), (2, 5), (3, 4), (3, 5), (4, 2), (4, 5)}.

Рис. 6.1. Пример сети

С каждым типом сети связан определенный тип потоков (например, транспорт­ный поток нефти в нефтепроводах или автомобильные потоки в сети городских до­рог). В общем случае потоки в сети ограничены пропускной способностью ее ребер, которая может быть как конечной, так и бесконечной.

Ребро называется направленным, или ориентированным (и в этом случае ребро будем называть дугой), если в одном направлении возможен только положитель­ный поток, а в противоположном — только нулевой. В ориентированной сети все ребра ориентированы.

Путем называется последовательность различных ребер, соединяющих два уз­ла, независимо от направления потока в каждом ребре. Путь формирует цикл, если начальный и конечный узлы совпадают. Например, на рис. 6.1 дуги (2, 3), (3, 4) и (4, 2) составляют цикл. Ориентированный цикл — это цикл, в котором все дуги ориентированы в определенном направлении.

Связная сеть — такая сеть, у которой любые два узла связаны по крайней мере одним путем. На рис. 6.1 показан именно такой тип сети. Деревом называется связная сеть, содержащая подмножество узлов исходной сети и не имеющая цик­лов. Остовное дерево'— это дерево, содержащее все узлы сети. На рис. 6.2 показа­ны дерево и остовное дерево для сети из рис. 6.1.

Дерево Остовное дерево

Рис. 6.2. Дерево и остовное дерево для сети из рис. 6.1

¹ Чтобы согласовать используемую здесь терминологию с терминологией теории графов, составляющей основу рассматриваемых сетей, будем называть дугами только ориентиро­ванные ребра. Термин "ребро" (как более общее понятие) часто будем употреблять для обо­значения как ребер, так и дуг. Также отметим очевидное соответствие между узлом сети и вершиной графа. — Прим. ред.

6.2. Алгоритм построения минимального остовного дерева

УПРАЖНЕНИЯ 6.1

1. Для каждой сети, показанной на рис. 6.3, определите: а) путь, б) цикл, в) ориентированный цикл, г) дерево, д) остовное дерево.

Рис. 6.3. Сети для упражнения 1

2. Определите множества N и А для сетей, представленных на рис. 6.3.

3. Нарисуйте сеть, заданную множествами

4. N = {1,2, 3,4, 5,6},

5. А = {(1, 2), (1, 5), (2, 3), (2, 4), (3, 5), (3, 4), (4, 3), (4, 6), (5, 2), (5, 6)}.

6. Дано восемь равных квадратиков, расположенных в три линии: на первой находится два квадратика, на второй — четыре и на третьей — два. Квадра­тики на каждой линии располагаются симметрично вертикальной оси. Необ­ходимо приписать каждому квадратику число от 1 до 8 так, чтобы смежные (по вертикали, горизонтали или диагонали) квадратики не имели последова­тельных номеров. Сформулируйте эту задачу как сетевую, и на основе сете­вого представления задачи разработайте алгоритм симметричного решения.

7. Троих заключенных в сопровождении трех стражников необходимо перепра­вить на лодке из Сан-Франциско в тюрьму на острове Алкатрас для исполнения приговора. Лодка не может перевести более двух человек одновременно. За­ключенные определенно сильнее стражников, если их количество в какой-то момент превысит количество стражников. Разработайте сетевую модель, по­зволяющую найти такую последовательность перевозки заключенных, чтобы не возникло каких-либо инцидентов между заключенными и стражниками.

6.2. АЛГОРИТМ ПОСТРОЕНИЯ МИНИМАЛЬНОГО ОСТОВНОГО ДЕРЕВА

Алгоритм построения минимального остовного дерева предполагает соединение всех узлов сети с помощью путей наименьшей длины. Типичной задачей, для реше­ния которой необходим такой алгоритм, является создание (проектирование) сети дорог с твердым покрытием, соединяющих населенные пункты в сельской местности, где дороги, соединяющие два каких-либо пункта, могут проходить через другие насе­ленные пункты. Наиболее экономичный проект дорожной системы должен миними­зировать общую длину дорог с твердым покрытием, при этом желаемый результат можно получить с помощью алгоритма построения минимального остовного дерева.

Опишем процедуру выполнения этого алгоритма. Обозначим через N = {1, 2, п} множество узлов сети и введем новые обозначения:

Глава 6. Сетевые модели

С_к — множество узлов сети, соединенных алгоритмом после выполнения k-й итерации этого алгоритма,

C_t — множество узлов сети, не соединенных с узлами множества С_к после вы­полнения k-й итерации этого алгоритма. Этап 0. Пусть С₀ = 0 и С₀ = N.

Этап 1. Выбираем любой узел i из множества С₀ и определяем С, = {i}, то­гда С, =N - {i}. Полагаем k = 2.

Основной этап к. В множестве С_к_₁ выбираем узел /, который соединен самой короткой дугой с каким-либо узлом из множества С_к__х. Узел / при­соединяется к множеству С_к__х и удаляется из множества С_к_₁. Та­ким образом, С_к = С_к_, + {;'*}, С, = Cj_, - {;'*}.

Если множество С_к пусто, то выполнение алгоритма заканчивается. В противном случае полагаем k — k + 1 и повторяем последний этап.

Пример 6.2.1

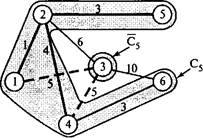
Телевизионная компания планирует подключение к своей кабельной сети пяти но­вых районов. На рис. 6.4 показана структура планируемой сети и расстояния (в милях) между районами и телецентром. Необходимо спланировать наиболее экономичную кабельную сеть.

Рис. 6.4. Кабельная сеть телевизионной компании

Чтобы начать выполнение алгоритма построения минимального остовного дерева, выберем узел 1 (или любой другой узел). Тогда

С,-{1}и С, ={2,3,4,5,6}.

Последовательные итерации выполнения алгоритма представлены на рис. 6.5. Здесь тонкими линиями показаны ребра, соединяющие узлы, принадлежащие множествам С* и C_t, среди которых ищется ребро с минимальной стоимостью

(длиной). Это найденное ребро показано пунктирной линией. Толстыми сплошны-•т линиями обозначены ребра, соединяющие узлы множества Q (и которые ранее)зн чались пунктирными линиями).

6.2. Алгоритм построения минимального остовного дерева

Итерация 1

Итерация 2

Итерация 3

Итерация 4

Итерация 5

Альтернативные ребра

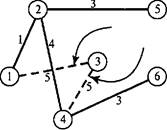
Итерация 6 (Минимальное остовное дерево)

Рис. 6.5. Последовательные итерации выполнения алгоритма построения минимального остовного дерева

Например, на первой итерации ребро (1,2) имеет наименьшую стоимость (т.е. наи­меньшее расстояние между пунктами сети) среди всех других ребер, соединяющих узел 1 с узлами множества С, (отметим, что узел 6 не имеет ребра, непосредственно

соединяющего его с узлом 1). Поэтому/ = 2 и С₂ = {1, 2}, С₂ = {3, 4, 5, 6}.

Решение в виде минимального остовного дерева получено на 6-й итерации (рис. 6.5). Минимальная длина кабеля для построения такой сети равна 1 + 3 + 4 + 4- 3 + 5 = 16 милям.

Глава 6. Сетевые модели

Программа TORA может находить минимальное остовное дерево. Для этого из меню Main menu выберите команду Network modelsOMinimal spanning tree (Сетевые моделиОМинимальное остовное дерево). Далее из меню SOLVE/MODIFY выберите команду Solve problemOGo to output screen (Решить задачу■=>Перейти к выходному окну). В выходном окне щелкните на кнопке Starting node (Начальный узел) и затем на кнопке Next iteration (Следующя итерация) или All iterations (Все итерации) для получения решения. Чтобы получить решение с новым начальным узлом, щелкни­те на кнопке Starting node. На рис. 6.6 показаны выходные результаты для задачи из примера 6.2.1 (файл ch6ToraMinSpanEx6-2-l.txt).

4Mb \wokUwattte>Vh61uie*Auttp«t«t / 1 ut

NETWORK MODEL¹-.

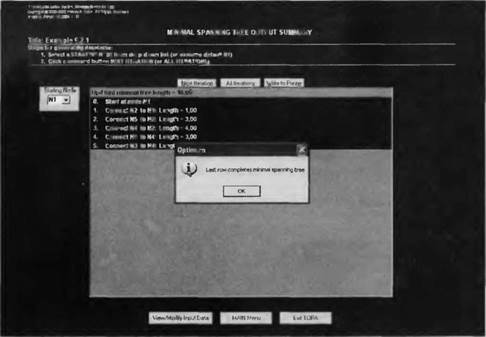
Рис. 6.6. Построенное минимальное остовное дерево для задачи из примера 6.2.1 УПРАЖНЕНИЯ 6.2

1. Решите задачу из примера 6.2.1, начиная с узла 5 (вместо узла 1), и убеди­тесь, что будет получено то же самое решение.

2. Найдите минимальное остовное дерево для сети из примера 6.2.1 при выпол­нении каждого из следующих условий в отдельности.

a) Узлы 5 и 6 связаны 2-мильным кабелем.

b) Узлы 2 и 5 не связаны.

c) Узлы 2 и 6 связаны 4-мильным кабелем.

d) Узлы 1 и 2 связаны кабелем длиной 8 миль.

e) Узлы 3 и 5 связаны кабелем длиной 2 мили.

f) Узел 2 не связан непосредственно с узлами 3 и 5.

6.2. Алгоритм построения минимального остовного дерева

3. В модульных перевозках груженые трейлерные платформы перевозятся по железной дороге между специальными перевалочными железнодорожными терминалами, где платформы снова присоединяются к трейлерам и далее следуют к потребителям по автомобильным дорогам. На рис. 6.7 показаны основные железнодорожные терминалы Соединенных Штатов и существую­щие железнодорожные пути между ними. Выделите сегменты железных до­рог так, чтобы связать все железнодорожные терминалы и минимизировать суммарную стоимость перевозок трейлерных платформ (стоимость перевозок пропорциональна длине железнодорожных путей).

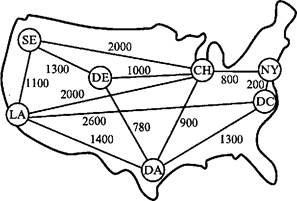
Рис. 6.7. Сеть для задачи из упражнения 3

4. На рис. 6.8 показаны расстояния между платформами, добывающими газ в открытом море, и приемным пунктом, расположенным на берегу. По­скольку платформа 1 ближе остальных к берегу, она оснащена необходимым оборудованием для перекачки газа от остальных платформ к приемному пункту. Спроектируйте сеть трубопроводов минимальной длины, соединяю­щую приемный пункт со всеми добывающими платформами.

Приемный пункт

Рис. 6.8. Сеть для задачи из упражнения 4

Глава 6. Сетевые модели

5. Предположим, что в предыдущей задаче (рис. 6.8) все добывающие платфор­мы разбиты на две группы в зависимости от давления газа в скважинах: к группе с высоким давлением газа относятся платформы 2, 3, 4 и 6, с низ­ким давлением — 5, 7, 8 и 9. Из-за разницы в давлении газопроводы от плат­форм разных групп нельзя соединять между собой. В то же время газопроводы от этих групп могут подсоединяться к приемному пункту через платформу 1. Определите минимальную сеть трубопроводов для данной ситуации.

6. Компания производит 15 типов изделий на 10 станках. Она планирует сгруп­пировать станки так, чтобы минимизировать "несходство" операций, вы­полняемых на каждой группе станков. Мерой "несходства" между станками i и у служит величина й_ц, вычисляемая по формуле

где п_ц — количество изделий, обрабатываемых как на станке i, так и на станке у, т_ц — количество изделий, обрабатываемых только на станке i или только на станке у.

В следующей таблице показано, изделия каких типов на каких станках обра­батываются.

Станок	Типы изделий
	1,6
	2, 3, 7, 8, 9, 12, 13, 15
	3, 5, 10, 14
	2, 7, 8,11,12,13
	3, 5, 10, 11, 14
	1,4, 5, 9, 10
	2, 5, 7, 9, 10
	3, 4, 15
	4, 10
	3, 8, 10, 14, 15

a) Сформулируйте данную задачу как сетевую.

b) Покажите, что разбить множество станков на группы можно, решив зада­чу нахождения минимального остовного дерева.

c) Решите данную задачу для разбиения станков на две и три группы.

6.3. ЗАДАЧА ПОИСКА КРАТЧАЙШЕГО ПУТИ

Данная задача состоит в определении в транспортной сети кратчайшего пути между заданными исходным пунктом и пунктом назначения. Такую модель можно использовать для описания разнообразных ситуаций, как показано в следующем разделе.

6.3. Задача поиска кратчайшего пути 251 6.3.1. Практические примеры задачи поиска кратчайшего пути

Пример 6.3.1. Замена оборудования

Компания по прокату автомобилей разрабатывает план по обновлению парка своих машин на следующие пять лет (2001-2005 гг.). Каждый автомобиль должен прора­ботать не менее одного и не более трех лет. В следующей таблице приведена стои­мость замены автомобиля в зависимости от года покупки и срока эксплуатации.

	Стоимость замены (долл.) в зависимости от срока эксплуатации
Год покупки
			—
		—	—

Задачу можно сформулировать как сетевую с пятью узлами с номерами от 1 до 5, соответствующими годам 2001-2005. Из узла 1 (2001 год) дуги идут только к узлам 2, 3 и 4, поскольку автомобиль может эксплуатироваться не менее одного и не бо­лее трех лет. Дуги из других узлов интерпретируются аналогично. Стоимости дуг равны стоимостям замены автомобилей. Решение задачи эквивалентно нахожде­нию кратчайшего пути между узлами 1 и 5.