Linear Programming Output summary 3 страница

х_х + х₂< 2, -jc, + х₂ < 4,

х_х — свободная переменная, х₂>0.

a) Найдите все допустимые базисные решения этой задачи.

b) С помощью подстановки решений в целевую функцию определите наи­лучшее базисное решение.

c) Решите эту задачу графическим способом и докажите, что решение, най­денное в предыдущем пункте, является оптимальным.

Глава 3. Симплекс-метод

3.3. АЛГОРИТМ СИМПЛЕКС-МЕТОДА

Основываясь на определениях из раздела 3.2, мы можем найти оптимальное решение задачи линейного программирования, записанной в стандартной форме, путем простого перебора всех базисных (допустимых) решений. Но, конечно, такая процедура не эффективна. Алгоритм симплекс-метода находит оптимальное реше­ние, рассматривая ограниченное количество допустимых базисных решений. В разделе 3.3.1 мы покажем итерационную природу симплекс-метода, а в разде­ле 3.3.2 — вычислительные детали его алгоритма.

3.3.1. Итерационная природа симплекс-метода

На рис. 3.3 показано пространство решений задачи ЛП из примера 3.2.1. Обыч­но алгоритм симплекс-метода начинается с исходной точки, где х_х = х₂ = 0 (точка А). В этой начальной точке значение целевой функции г равно нулю. Возни­кает естественный вопрос: если одна или обе небазисные переменные х_х и х₂ примут положительные значения, то приведет ли это к улучшению (возрастанию) значений целевой функции? Для ответа на этот вопрос рассмотрим целевую функцию

максимизировать г = 2х_х + Зх₂.

Очевидно, что если переменная х_х или переменная х₂ (или обе сразу) примут положи­тельные значения, то это приведет к увеличению значения целевой функции (помните, что рассматривается задача максимизации). Однако алгоритм симплекс-метода на каждом шаге допускает изменение значения только одной небазисной переменной.

1. Если увеличивать значение переменной x_v то (см. рис. 3.3) ее значение должно возрасти таким образом, чтобы соответствовать угловой точке В (повторим, что внутренние точки отрезка от точки А до точки В неприемле­мы, поскольку кандидатом на оптимальное решение может быть только уг­ловая точка). В точке В симплекс-метод должен увеличить значение пере­менной х₂, перемещаясь при этом в угловую точку С. Так как точка С соответствует оптимальному решению, то на этом процесс вычислений за­канчивается. Таким образом, алгоритм симплекс-метода создает путь А—> В —» С.

2. Если сначала увеличивать значение переменной х₂, то следующей угловой точкой будет точка D, из которой процесс решения переходит в оптимальную точку С. Здесь алгоритм симплекс-метода создает путь А —> Z) —»С.

Отметим, что оба пути, A^>B—>CnA—>D—>C, расположены вдоль границы про­странства решений. Это означает, что симплекс-метод не может сразу перескочить из точки А в точку С.

Может возникнуть правомерный вопрос: существует ли правило, в соответствии с которым можно было бы определить, какую небазисную переменную сделать по­ложительной в данной угловой точке? Например, в точкеА как переменная x_v так и переменная х₂ могут увеличить значение целевой функции. Симплекс-метод предлагает простое правило выбора переменных, которое в основном применяется в его программных реализациях. Поскольку здесь мы рассматриваем задачу мак­симизации, то следует выбирать такую небазисную переменную, которая имеет наибольший положительный коэффициент в выражении целевой функции. Если таких переменных несколько, то выбор произвольный. Необходимо понимать, что это эмпирическое правило, сформулированное на основе многочисленных компью­терных вычислений симплекс-метода — в большинстве случаев (но не обязательно всегда) применение этого правила ведет к наименьшему числу итераций, затрачи­ваемых на поиск оптимального решения.

3.3. Алгоритм симплекс-метода

0 1 2 3 4 5 *i

Рис. 3.3. Итерационный процесс симплекс-метода

Этот раздел завершим описанием перевода небазисных переменных в базисные и наоборот при переходе от одной угловой точки к следующей. На рис. 3.4 показано, что в точке А переменные s, и s₂ являются базисными, а переменные я, и х₂ — неба­зисными. Если переменная jc, принимает положительное значение, мы переходим в угловую точку В, в которой изменяется состояние переменной х_х из небазисной в ба­зисную. Одновременно переменная s,, которая была базисной в точкеА, становится небазисной и принимает нулевое значение в точке В. Здесь существенно, что проис­ходит одновременный "обмен состояниями" между небазисной переменной х_г и ба­зисной переменной s,, что приводит к новым базисным переменным (*,, s₂) и небазис­ным переменным (s,, х₂) в точке В. Скажем, что в точкеА переменная x_t вводится в базисное решение, а переменная s, — исключается из базисного решения. В соот­ветствии с терминологиейсимплекс-метода выбранная небазисная (нулевая) пере­менная называется вводимой (в базисное решение), а удаляемая (из базисного реше­ния) базисная переменная— исключаемой. В точке В вводимой и исключаемой переменными будут соответственно переменные х₂ и s₂. Процесс изменения состояний переменных заканчивается в точке С, поскольку найдено оптимальное решение.

УПРАЖНЕНИЯ 3.3.1

1. На рис. 3.4 показана схема изменения базисных и небазисных переменных в соответствии с путем А—> В —> С в пространстве решений, представленном на рис. 3.3. Создайте аналогичную схему для пути А—> D —» С.

2. Вернитесь к графическому решению задачи Reddy Mikks, показанному на рис. 2.2. Разработайте схему изменения базисных и небазисных переменных (подобную представленной на рис. 3.4), указав на каждой итерации вводи­мые и исключаемые переменные в соответствии со следующими путями.

a) А->В->С.

b) А-> F -> Е -> D -> С.

Глава 3. Симплекс-метод

Точка А

Точка В

Точка С

Небазисные переменные

(*1> *г)

-1-

х₁ вводится

<>l> s₂)

Базисные переменные

х₂ вводится

Y Y

s_i исключается s₂ исключается Оптимум

Рис. 3.4. Вводимые и исключаемые переменные в симплекс-методе

3. На рис. 3.5 показано пространство допустимых решений трехмерной задачи ЛП с угловыми точками А, В, С, J.

a) Могут ли следующие пары угловых точек составить часть пути при успешном выполнении симплекс-метода: (А, В), (В, D), (Е, Н), (А, 1)7 Поясните ответ.

b) Предположим, что реализация симплекс-метода начинается в точке А и заканчивается в точке оптимума Н. Определите, какие из следующих последовательностей угловых точек могут привести к точке оптимума. Обоснуйте свой вывод.

i) А-> B->G-> Н.

ii) А^>С-> 1^>Н.

in) A->C->£->£->A->Z)->G->#.

G

Рис. 3.5. Пространство решений для задачи ЛП

4. Пусть в задаче ЛП, которой соответствует пространство допустимых реше­ний, показанное на рис. 3.5, все ограничения являются неравенствами типа "<", а все переменные задачи (т.е. x_v х_г и х₃) неотрицательны. Обозначим че­рез s,, s₂, s₃ и s₄ дополнительные (неотрицательные) переменные, ассоции­

3.3. Алгоритм симплекс-метода

руемые с ограничениями, представленными плоскостями CEIJF, BEIHG, DFJHG и IJH соответственно. Определите базисные и небазисные перемен­ные для каждой угловой точки пространства допустимых решений.

5. Пусть в задаче ЛП, для которой пространство допустимых решений представле­но на рис. 3.5, реализация симплекс-метода начинается в точке А. Определите вводимую переменную на первой итерации симплекс-метода, а также ее значение и значение целевой функции, если целевая функция имеет следующий вид.

a) Максимизировать г — х₁- 2х₂ + Зх₃.

b) Максимизировать г = 5л:, + 2х₂ + 4х₃.

c) Максимизировать z = -2х₁ + 7х₂ + 2х₃.

d) Максимизировать z — х_у + х₂ + х₃.

3.3.2. Вычислительный алгоритм симплекс-метода

В этом разделе показаны вычислительные свойства алгоритма симплекс-метода, которые включают правила для определения вводимых и исключаемых перемен­ных, а также условия достижения оптимального решения, при которых вычисле­ния завершаются. Рассмотрим числовой пример.

Пример 3.3.1

Используем задачу о компании Reddy Mikks (пример 2.2.1) для рассмотрения дета­лей выполнения симплекс-метода. Эта задача в стандартной форме записывается так:

максимизировать z = 5дс, + 4х₂ + 0s, + 0s₂ + 0s₃ + 0s₄

при ограничениях

6xi + 4х₂ + si = 24 (ограничение на сырье М1), xi + 2x2 + s₂ = 6 (ограничение на сырье М2), -*1 + Хг + вз = 1 (ограничение на спрос), хг + s₄ = 2 (ограничение на спрос),

Хи Хг, Si, S2, S3, Si > 0.

Здесь s_v s₂, s₃, s_t — дополнительные (остаточные) переменные, добавленные в нера­венства для преобразования их в равенства.

Далее целевую функцию будем представлять в виде уравнения

г - 5д:, - 4х₂ = 0.

Задачу ЛП в стандартной форме можно представить в виде следующей компактной таблицы.

Базис	Z	*1	Хг	S1	S2	S3	&t	Решение
z		-5	-4						z-строка
S1									Si-строка
S2									вг-строка
s3		-1				lllSfl			вз-строка
S4									54-строка

Глава 3. Симплекс-метод

Таблица показывает множества базисных и небазисных переменных, а также ре­шение, соответствующее данной (начальной) итерации. В разделе 3.3.1 указыва­лось, что начальная итерация симплекс-метода начинается из точки (*,, х₂) = (0, 0). Это соответствует следующим множествам базисных и небазисных переменных.

Небазисные (нулевые) переменные: (jc,, х₂).

Базисные переменные: (s_v s₂, s₃, s_t).

Поскольку небазисные переменные х_х,х_г и коэффициенты при базисных перемен­ных s_v s₂, s₃, s₄ в уравнении целевой функции равны нулю, а в формулах левых час­тей равенств-ограничений — 1, то отсюда сразу без дополнительных вычислений получаем, что z — 0,s₁ = 24, s₂ = 6, s₃ = 1 и s_t = 2.

В таблице базисные переменные перечислены в левом столбце "Базис", а их значе­ния приведены в правом столбце "Решение". Таким образом, в таблице текущая угловая точка определяется путем указания базисных переменных и их значений, а также вычисляется соответствующее значение целевой функции 2. Помните, что не­базисные переменные (которые не приведены в столбце "Базис") всегда равны нулю.

Будет ли это начальное решение оптимальным? Конечно, нет, поскольку переменные *, и х₂ здесь равны нулю, а возрастание этих переменных даже на единицу приводит к увеличению значения целевой функции z= 5дг, + 4х₂ на 5 (при увеличении *,) или 4 (при увеличении х₂). Поскольку коэффициент при переменной *, в формуле целевой функции больше, чем коэффициент при х_г, переменную *, следует ввести в число базис­ных (в этом случае она станет вводимой). Если обратиться к приведенной выше таблице, то вводимая переменная определяется среди множества небазисных как переменная, имеющая наибольший отрицательный коэффициент в z-строке (напомним, что тут решается задача максимизации). Если так случится, что все коэффициенты в z-строке будут неотрицательными, то дальнейшее увеличение значения целевой функции бу­дет невозможно; это будет означать, что достигнуто оптимальное решение.

Чтобы определить исключаемую переменную непосредственно из таблицы, надо вычислить точки пересечения всех функций ограничений с положительным на­правлением оси *, (повторим, что переменная *, уже определена как вводимая пе­ременная). Координаты этих точек пересечения можно вычислить как отношения правых частей равенс.тв (значение в столбце "Решение") к коэффициентам при пе­ременной*, в этих равенствах, как показано в следующей таблице.

Базис	Коэффициенты при *1	Решение	Отношение (точка пересечения)
«1			х, = 24/6 = 4 (минимум)
s2			х, =6/1=6
s3	-1		Xi = 1/(-1) = -1 (не подходит)
s4			xi = 2/0 = °° (не подходит)

На рис. 3.6 видно, что неотрицательные отношения порождают точки пересечения на положительной полуоси Отношения (пересечения), соответствующие пере­менным s₃ и s_t, исключаются из рассмотрения, поскольку для них точка пересече­ния лежит или на отрицательной полуоси, или на бесконечности.

Минимальное неотрицательное отношение соответствует базисной переменной s_v тем самым определяя эту переменную как исключаемую (т.е. на следующей итера­ции ее значение будет равно нулю). Значение вводимой переменной *, в новом

3.3. Алгоритм симплекс-метода

решении также равно минимальному неотрицательному отношению, а именно дс, = 4 (сравните с точкой В на рис. 3.6). Значение целевой функции при этом значе­нии;c, возрастет до 20 (= 5x4).

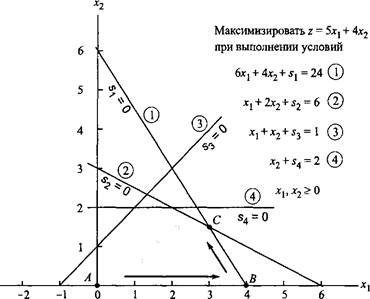
Рис. 3.6. Графическая интерпретация отношений как точек пересечения

Замена исключаемой переменной на вводимую переменную дс, приводит к новым множествам базисных и небазисных переменных и новому решению в точке В.

Небазисные (нулевые) переменные: (s,, дг₂).

Базисные переменные: (д,, s₂, s₃, s_t).

Теперь необходимо выполнить преобразования в последней таблице так, чтобы в столбцах "Базис" и "Решения" получить новое решение, соответствующее точ­ке В. Вычисление нового базисного решения основывается на методе исключения переменных (методе Гаусса-Жордана), который описан в разделе А.2.7. Эти вы­числения громоздкие и объемные, что делает компьютер незаменимым средством для решения задач линейного программирования. Вы должны освоить ручной спо­соб вычислений хотя бы для того, чтобы понять, как работает симплекс-метод. По­сле этого, вы, вероятно, никогда не будете выполнять вычисления вручную.

В следующей таблице, которая пока совпадает с начальной таблицей задачи ЛП, определим ведущий столбец, ассоциируемый с вводимой переменной, и ведущую строку, ассоциируемую с исключаемой переменной. Элемент, находящийся на пересечении ведущего столбца и ведущей строки, назовем ведущим.

Глава 3. Симплекс-метод

	Базис	z	Xl	X2	Si	s2	S3	S4	Решение
	z		-5	-4
<—	S1									Ведущая строка
	s2
	S3		-1
	S4

Ведущий столбец

Процесс вычисления нового базисного решения состоит из двух этапов.

1. Вычисление элементов новой ведущей строки.

Новая ведущая строка = текущая ведущая строка / ведущий элемент.

2. Вычисление элементов остальных строк, включая z-строку.

Новая строка = текущая строка - ее коэффициент в ведущем столбце х новая ве­дущая строка.

В нашем примере выполняем такие вычисления.

1. Новая ведущая.^-строка = текущая ведущая.^-строка / 6.

2. Новая z-строка = текущая z-строка - (-5) х новая ведущая строка.

3. Новая.^-строка = текущая зустрока - (1) х новая ведущая строка.

4. Новая jycTpoKa = текущая ^-строка - (-1) х новая ведущая строка.

5. Новая л-₄-строка = текущая.^-строка - (0) х новая ведущая строка.

Новая симплекс-таблица, соответствующая новому базисному решению (x_v s₂, s₃, s_t), имеет следующий вид (проверьте результаты вычислений!).

Базис	Z	' х,	Хг	S1	S2	S3	S4	Решение
z			-2/3	5/6
х-			2/3	1/6
<- S2			4/3	-1/6	113Я			шшшшш
S3			1.5/3 4	1/6
S4			.- 1.

Отметим, что новая таблица обладает теми же свойствами, что и начальная: только небазисные переменные х_г и s_x равны нулю, в столбце "Решение" представлено но­вое базисное решение (х₁ = 4, s₂ = 2, s₃ — 5, s_t = 2) вместе с новым значением целевой функции z (= 20). Это результат применения метода Гаусса-Жордана.

Из последней таблицы видно, что полученное базисное решение не является опти­мальным, поскольку в z-строке переменная х_г имеет отрицательный коэффициент. Как и в начальной таблице, строку z можно интерпретировать как уравнение

3.3. Алгоритм симплекс-метода

2 5 z=-x,—s. +20.

3 " 6 '

Из последнего уравнения следует, что увеличение значения переменной х₂ (ее те­кущее значение равно нулю) приведет к увеличению значения целевой функции. Таким образом, переменная х₂ должна стать вводимой в базис.

Далее определим исключаемую переменную. Для этого вычислим отношения пра­вых частей равенств, соответствующих ограничениям, к коэффициентам, стоящим прих, в этих равенствах.

Базис	Коэффициенты при х2	Решение		Отношение
*1	2/3		хг	= 4/(2/3) = 6
s2	4/3		Хг	= 2/(4/3) = 3/2 (минимум)
s3	5/3		Х2	= 5/(5/3) = 3
St			Х2	= 2/1=2

Вычисления показывают, что минимальное (неотрицательное) отношение соответ­ствует переменной s₂, которая становится исключаемой; при этом значение отно­шения (= 3/2) равно новому значению переменной х₂. Соответствующее увеличение

2 3

значения целевой функции составит —х — = 1 hz = 20 + 1 = 21.

В этой ситуации ведущей строкой будет ^-строка, а ведущим столбцом — столбец, соответствующий переменной х₂. Ведущий элемент равен 4/3.

Вычисляем элементы новой симплекс-таблицы.

1. Новая ведущая,у₂-строка = текущая.^-строка / —.

2. Новая строка z-строка = текущая z-строка - (- —) х новая ведущая строка.

3. Новая jCj-строка = текущая л^-строка - -j х новая ведущая строка.

4. Новая.^-строка = текущая.^-строка - — х новая ведущая строка.

5. Новая.у₄-строка = текущая ^-строка - 1 х новая ведущая строка. Эти вычисления приводят к следующей таблице.

Базис	Z	Xi	Хг	S1	S2	S3	S4	Решение
z				3/4	1/2
				1/4	-1/2
хг				-1/8	3/4			3/2
S3				3/8	-5/4			5/2
S4				1/8	-3/4			1/2

Поскольку z-строка не имеет отрицательных коэффициентов, соответствующих небазисным переменным s_x и s₂, полученное решение оптимально.

Глава 3. Симплекс-метод

Оптимальное решение задачи ЛП можно "считать" из симплекс-таблицы следующим образом. Неотрицательные (базисные) переменные представлены в столбце "Базис", а их значения— в столбце "Решение". В данном примере имеем следующее.

Переменные задачи	Оптимальные значения	Интерпретация
		Ежедневно следует производить 3 т краски для наружных работ
хг	3/2	Ежедневно следует производить 1,5 т краски для внутренних работ
z		Ежедневный доход составляет 21 тыс. долл.
Вы можете s3 = 5/2 hs4 =	проверить, что значения дополнительных переменных 5, = s2 = 0, 1/2 согласуются со значениями переменных х, и х2.

С помощью симплекс-таблицы можно получить много дополнительной инфор­мации (кроме непосредственно оптимального решения).

1. Состояние ресурсов.

2. Цена единицы ресурсов (двойственные цены).

3. Все данные, необходимые для проведения анализа чувствительности опти­мального решения.

Здесь мы покажем, как определить состояние (статус) ресурсов. Вычисление двойственных цен и использование данных симплекс-таблицы для проведения анализа чувствительности описано в главе 4.

Статус ресурса определяется как дефицитный или недефицитный, в зависимости от того, будет он использован полностью или нет. Эту информацию можно получить из ре­зультирующей симплекс-таблицы путем проверки значений дополнительных (остаточных) переменных, ассоциируемых с соответствующими ограничениями, нала­гаемыми на ресурсы. Если дополнительная переменная равно нулю, значит, ресурс ис­пользован полностью, и он получает статус дефицитного. Положительное значение до­полнительной переменной указывает на недефицитность соответствующего ресурса.

В задаче о компании Reddy Mikks четыре ограничения классифицируются сле­дующим образом.

Ресурс	Остаточная переменная	Статус
Сырье М1	Si =0	Дефицитный
Сырье М2	s2 = 0	Дефицитный
Ограничение на спрос 1	S3 = 2,5	Недефицитный
Ограничение на спрос 2	Si = 0,5	Недефицитный

Статус ресурсов показывает, что, поскольку Ml и М2 дефицитны, их увеличение может привести к улучшению оптимального решения (т.е. увеличению значения целевой функции). Процедура анализа чувствительности поможет определить, на сколько можно увеличить объемы ресурсов. Этот вопрос исследовался в разделах 2.3.2 и 2.3.3, полное его решение представлено в главе 4.

3.3. Алгоритм симплекс-метода

В примере 3.3.1 велся поиск максимума целевой функции. В случае минимизации целевой функции исключаемые переменные определяются точно так же, как и при ее максимизации. Поскольку задача минимизации сводится к задаче максимизации простым соотношением max z = - min(-z), то в случае минимизации целевой функ­ции вводимая переменная выбирается как небазисная с наибольшим положитель­ным коэффициентом в z-строке симплекс-таблицы, а минимум целевой функции бу­дет достигнут тогда, когда все коэффициенты в z-строке будут неположительными.

Два правила выбора вводимых и исключающих переменных в симплекс-методе назовем условием оптимальности и условием допустимости. Сформулируем эти правила, а также рассмотрим последовательность действий, выполняемых при реализации симплекс-метода.

Условие оптимальности. Вводимой переменной в задаче максимизации (минимизации) является небазисная переменная, имеющая наибольший отрица­тельный (положительный) коэффициент в z-строке. Если в z-строке есть несколько таких коэффициентов, то выбор вводимой переменной делается произвольно. Оп­тимальное решение достигнуто тогда, когда в z-строке все коэффициенты при неба­зисных переменных будут неотрицательными (неположительными).

Условие допустимости. Как в задаче максимизации, так и в задаче минимиза­ции в качестве исключаемой выбирается базисная переменная, для которой поло­жительное отношение значения правой части ограничения к положительному ко­эффициенту ведущего столбца минимально. Если базисных переменных с таким свойством несколько, то выбор исключаемой переменной выполняется произвольно.

Теперь приведем последовательность действий, выполняемых в симплекс-методе.

Этап 0. Находится начальное допустимое базисное решение.

Этап 1. На основе условия оптимальности определяется вводимая перемен­ная. Если вводимых переменных нет, вычисления заканчиваются.

Этап 2. На основе условия допустимости выбирается исключаемая пе­ременная.

Этап 3. Методом Гаусса-Жордана вычисляется новое базисное решение. Переход к п. 1.

УПРАЖНЕНИЯ 3.3.2

1. Это упражнение должно показать значимую роль условия допустимости в симплекс-методе. В примере 3.3.1 в первой симплекс-таблице мы исполь­зовали минимальное неотрицательное значение из множества вычисленных отношений для определения исключаемой переменной. Такой выбор исклю­чаемой переменной гарантирует, что новое значение базисной переменной не будет отрицательным. Для иллюстрации этого утверждения на первом шаге вместо переменной s, исключите из базисного решения переменную s₂. Далее посмотрите на результирующую симплекс-таблицу, вы должны увидеть, что переменная s, приняла отрицательное значение (= -12). Это показывает, что полученное решение недопустимо.

2. Рассмотрим следующее множество ограничений.

x, + 2a;₂-2a;₃ + 4a;₄<40, 2х_х - х₂ + х₃ + 2x_t < 8, 4jc, - 2х₂ + х₃- x_t< 10,.х,, х₂, х₃, х^ — 0.

Глава 3. Симплекс-метод

С учетом этих ограничений решите следующие задачи ЛП.

a) Максимизировать г = 2х, + х₂ - Зх₃ + 5х₄.

b) Максимизировать г = 8х, + 6х₂ + Зх₃ - 2x_t.

c) Максимизировать г = Зх, - х₂+ Зх₃ + 4х₄.

d) Минимизировать г — 5х, - 4х₂ + 6х₃ - 8х₄.

e) Минимизировать г = -4х, + 6х₂ - 2х₃ + 4х₄.

3. Дана следующая система уравнений: