Gifford

• Алгоритм использует единственный 8-байтовый регистр:

b0, b1,...., b7.

• Ключом является начальное состояние регистра.

• Открытый текст не влияет на работу алгоритма. Для генерации байта ключа k объединим b0 и b1, а также объединим b4 и b7.

• Перемножим полученные числа, получая 32-битовое число.

• Третьим слева байтом и будет k.

• Для обновления регистра возьмем b1 и сдвинем вправо ''с приклеиванием'' на 1 бит следующим образом: крайний левый бит одновременно и сдвигается, и остается на месте.

• Возьмем b7 и сдвинем его на один бит влево, в крайней правой позиции должен появиться 0.

• Выполним XOR измененного b1, измененного b7 и b0. Сдвинем первоначальный байт регистра на 1 бит вправо и поместим этот байт в крайнюю левую позицию.

• В течение всего времени использования этот алгоритм оставался безопасным, но он был взломан в 1994 году. Оказалось, что многочлен обратной связи не был примитивным и, таким образом мог быть вскрыт.

PKZIP

• Использует три 32-битовых переменных:

• К0 = 305419896; К1 = 591751049; К2 = 878082192.

• Используется 8-битовый ключ К3, полученный из К2.

Алгоритм (в стандартной нотации С):

Сi=Рi^K3;

K0=сrc32 (K0,Pi);

K1=K1+ (K0 & 0х000000ff);

K1= K1*134775813 + 1;

K2 = сrc32 (K2, K1 >> 24);

K3 = ((K2|2)*((K2 | 2)^1))>>8.

Функция crc32 берёт своё предыдущее значение и байт, выполняет их XOR и вычисляет следующее значение с помощью многочлена CRC, определённого 0xcdb88320.

На практике 256-элементная таблица может быть рассчитана заранее, и вычисление crc32 превращается в

crc32(a,b)=(a<<8)^ table [(a& 0xff) xor b].

Для шифрования потока открытого текста сначала для обновления ключей зациклим байты ключа в алгоритме шифрования.

Полученный шифротекст на этом этапе игнорируется.

Затем побайтно зашифруем открытый текст. Открытому тексту предшествуют 12 случайных байт, но это не важно.

Безопасность этого алгоритма не слишком велика. Для вскрытия нужно от 40 до 2000 байтов известного открытого текста.Если в сжатом файле используются стандартные заголовки, то вскрытие становится ещё прощё.

1. Примеры поточных шифров на основе FCSR.

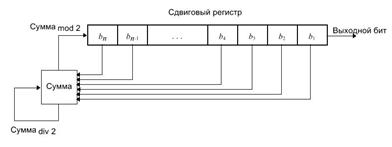
• Сдвиговый регистр с обратной связью по переносу, или FCSR (feedback with carry shift register), похож на LFSR

• В обоих есть сдвиговый регистр и функция обратной связи, разница в том, что в FCSR есть также регистр переноса.

• Вместо выполнения XOR над всеми битами отводной последовательности эти биты складываются друг с другом и с содержимым регистра переноса.

• Результат mod 2 и становится новым битом.

• Результат, деленный на 2, становится новым содержимым регистра переноса.

• Регистр переноса не бит, а число.

• Максимальный период FCSR выше, чем LFSR. Любое начальное состояние приводит к одной из четырёх ситуаций. Во-первых, оно может быть частью максимального периода. Во вторых, оно может перейти в последовательность максимального периода после начальной задержки. В третьих, после начальной задержки оно может породить бесконечную последовательность нулей. В четвёртых, после начальной задержки оно может породить бесконечную последовательность единиц. Для определения, чем закончится конкретное начальное состояние, существует математическая формула, но намного проще проверить это опытным путём. Если выходной поток вырождается в бесконечную последовательность нулей или единиц за n битов, где n - длина FCSR, не используйте это начальное состояние. FCSR можно использовать в потоковых шифрах вместо LFSR, а можно комбинировать FCSR и LFSR,например:

• Каскад FCSR. Каскад Голлманна с FCSR вместо LFSR;

• Каскад LFSR/ FCSR. Каскад Голлманна с генераторами, меняющими LFSR на FCSR и наоборот;

• Генератор "стоп - пошёл " FCSR. Все регистры - CSR; объединяющая функция XOR.

• Генератор "стоп - пошёл " FCSR/LFSR.Регистр-1 - CSR, а Регистр-2 и Регистр-3 - LFSR. Объединяющая функция - сложение с переносом

RC4

• Поток ключей в этом алгоритме не зависит от открытого текста.

• Используется S-блок размером 8*8: S(0),....,S(255)

• Элементы представляют собой перестановку чисел от 0 до 255, а перестановка является функцией ключа переменной длины.

• В алгоритме применяются два счётчика (i и j) с нулевыми начальными значениями.

• Для генерации случайного байта выполняется следующее:

• i = (i+1) mod 256; j = (i+ S(i))) mod 256;

• меняем местами S(i) и S(j);

• t = (S(i) + S(j)) mod 256; K = S(t).

• Байт K используется в операции XOR с открытым текстом для получения шифротекста.

• Шифрование выполняется примерно в 10 раз быстрее, чем DES.

Инициализация S блока.

• Сначала заполним его линейно: S(0)=0;....;S(255)=255.

• Затем заполним ключом другой 256-байтовый массив, при необходимости для заполнения всего массива повторяя ключ: K(0),...,K(255).

• Установим j=0.

• for(i=0;i<256;i++)

{

j=(j+S(i)+K(i)) mod 256;

меняем местами S(i) и S(j);

}

Утверждается, что алгоритм устойчив к дифференциальному и линейному криптоанализу, что в нём нет никаких коротких циклов, и что он в высокой степени нелинеен.

RC4 может находиться в 21700 возможных состояниях.

S-блок медленно изменяется при использовании: i обеспечивает изменение каждого элемента, а j - что элементы изменяются случайным образом.

Идею можно обобщить на S-блоки и слова больших размеров.

WAKE

• Алгоритм WAKE(Word Auto Key Encryption) выдаёт поток 32-битных слов,которые с помощью XOR могут быть использованы для получения шифротекста.

• Для генерации следующего слова ключа используется предыдущее слово шифротекста.

• Это быстрый алгоритм.

• Алгоритм также использует S блок из 256 32-битовых значений. Этот S-блок обладает одним особым свойством: старший байт всех элементов представляет собой перестановку всех возможных байтов, а 3 младших байта случайны.

• Сначала по ключу сгенерируем элементы S-блока.

• Затем проинициализируем четыре регистра с использованием того же или иного ключа: A(0),B(0),C(0) и D(0).

• Для генерации слова потока ключей K(i): K(i)=D(i).

• Слово шифротекста С(i) представляет собой XOR слова открытого текста P(i) c K(i).

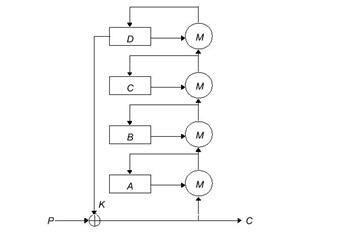
• Затем обновим четыре регистра:

A(i+1) = M(A(i),D(i));

B(i+1) = M(B(i),A(i+1));

C(i+1) = M(C(i),B(i+1));

• D(i+1) = M(D(i),C(i+1)), где M(x,y)= (x+y) >> 8 xor S((x+y)^255).

• Самым ценным качеством WAKE является его скорость. Однако он чувствителен к вскрытию с выбранным открытым текстом или выбранным шифротекстом.

1. Математические методы криптоанализа: метод опробывания, методы на основе теории статистических решений.

Криптоанализ включает определение используемого языка, типа криптосистемы, ключа и исходного текста; обычно именно в этом порядке

Попытку раскрытия конкретного шифра с применением методов криптоанализа называют криптографической атакой на этот шифр. Криптографическую атаку, в ходе которой раскрыть шифр удалось, называют взломом или вскрытием.

Метод «опробывания» (полного перебора, brute force).

V – алфавит

N – его мощность(кол-во букв)

X = (x₁, x₂, …, x_n) ϵ V_n

k^o = (k₁^o, …, k_l^o) ϵ K c V^l_n – ключ данного сеанса шифрования

f(●) – функция зашифрования

y = (y₁, …, y_n) ϵ Vⁿ_N -шифр текст (С)

y = f(X, k^o)

x = f^-1(y, k) -расшифровка

1. Линейный криптоанализ.

Линейный криптоанализ изначально разрабатывался для атак на блочные шифры, но применим и к потоковым. Самим разработчиком было подробно изучено его применение к DES.

Криптоанализ происходит в два шага. Первый — построение соотношений между открытым текстом, шифротекстом и ключом, которые справедливы с высокой вероятностью. Второй — использование этих соотношений вместе с известными парами открытый текст — шифротекст для получения битов ключа.

Смысл алгоритма состоит в получении соотношений следующего вида:

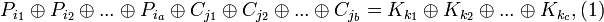
где P_n, C_n, K_n — n-ые биты текста, шифротекста и ключа.

Данные соотношения называются линейными аппроксимациями. Для произвольно выбранных бит открытого текста, шифротекста и ключа вероятность справедливости такого соотношения P примерно равна 1/2. Такими соотношениями, вероятность которых заметно отличается от 1/2 можно пользоваться для вскрытия алгоритма.

Как и в дифференциальном криптоанализе, сначала криптоаналитик находит некое однораундовое соотношение, затем пытается распространить его на весь алгоритм. В отличие от дифференциального криптоанализа существуют алгоритмы поиска полезных соотношений. Два алгоритма были описаны Мицуру Мацуи, другие появились позже.

В блочных шифрах анализ преимущественно концентрируется на S-боксах, так как они являются нелинейной частью шифра. Наиболее эффективное однораундовое соотношение для алгоритма DES использует свойство таблицы S5. Второй входной бит таблицы равен результату операции XOR над всеми выходными битами с вероятностью 3/16 (смещение в 5/16 относительно 1/2). А для полнораундового DES известно соотношение, выполняющееся с вероятностью 1/2 + 2⁻²⁴.

Линейный криптоанализ имеет одно очень полезное свойство — при определённых условиях можно свести соотношение (1) к уравнению вида:

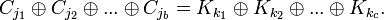
Здесь отсутствуют биты открытого текста, то есть можно построить атаку на основе только шифротекста. Такая атака является наиболее практичной.