 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Система випадкових величин. 2. Закон розподілу двохвимірної ДВВ
|
|
2. Закон розподілу двохвимірної ДВВ.
3. Функції розподілу двохвимірної ВВ. Залежність та незалежність ВВ.
4. Числові характеристики двохвимірної ВВ.
5. Функції ВВ та їх характеристики.
Нехай 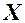 - НВВ, закон розподілу якої заданий диференціальною функцією (щільністю розподілу імовірностей)
- НВВ, закон розподілу якої заданий диференціальною функцією (щільністю розподілу імовірностей) 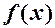 , а ВВ
, а ВВ 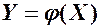 . Якщо
. Якщо 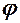 - диференційовна функція, монотонна на усьому проміжку можливих значень
- диференційовна функція, монотонна на усьому проміжку можливих значень 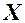 , то щільність розподілу функції
, то щільність розподілу функції 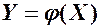 визначається за формулою:
визначається за формулою:
 , (*)
, (*)
де 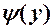 - функція, обернена до функції
- функція, обернена до функції 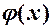 .
.
Алгоритм знаходження щільності розподілу  .
.
1. Визначити множину можливих значень для 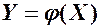 .
.
2. Із функціональної залежності 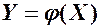 знайти явний вираз
знайти явний вираз 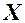 через
через  , тобто функцію
, тобто функцію 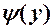 , обернену до функції
, обернену до функції 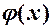 .
.
3. Знайти похідну 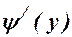 .
.
4. За формулою (*) записати щільність розподілу ВВ  .
.
5. Перевірити умову нормування для  :
: 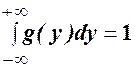 .
.
ЗАДАЧІ ДЛЯ РОЗВ’ЯЗУВАННЯ В АУДИТОРІЇ
Приклад 7.1. Знайти закони розподілу компонент двохвимірної ВВ, закон розподілу якої заданий таблицею:
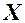
| 
| |
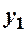
| 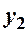
| |
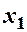
| 0,01 | 0,07 |
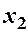
| 0,25 | 0,28 |

| 0,12 | 0,27 |
Приклад 7.2. ДВВ 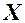 задана таблицею
задана таблицею
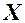
| -2 | ||
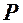
| 0,2 | 0,3 | 0,5 |
Знайти закон розподілу та числові характеристики функції 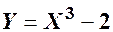 .
.
Приклад 7.3. ВВ 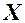 розподілена за нормальним законом з математичним сподіванням
розподілена за нормальним законом з математичним сподіванням 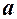 та середнім квадратичним відхиленням
та середнім квадратичним відхиленням 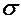 . Знайти закон розподілу функції
. Знайти закон розподілу функції 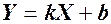 .
.
Приклад 7.4. ВВ 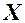 рівномірно розподілена на [-1;1]. Знайти закон розподілу функції
рівномірно розподілена на [-1;1]. Знайти закон розподілу функції 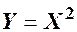 .
.
ЗАДАЧІ ДЛЯ САМОСТІЙНОГО РОЗВ’ЯЗУВАННЯ
Приклад 7.5. Знайти закони розподілу компонент двохвимірної ВВ, закон розподілу якої заданий таблицею:
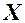
| 
| |
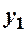
| 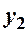
| |
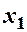
| 0,27 | 0,25 |
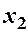
| 0,07 | 0,12 |

| 0,28 | 0,01 |
Приклад 7.6. ДВВ 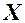 задана таблицею
задана таблицею
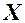
| -1 | ||
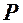
| 0,3 | 0,1 | 0,6 |
Знайти закон розподілу та числові характеристики функції 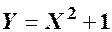 .
.
Приклад 7.7. ВВ 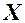 розподілена за нормальним законом з математичним сподіванням
розподілена за нормальним законом з математичним сподіванням 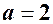 та середнім квадратичним відхиленням
та середнім квадратичним відхиленням 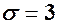 . Знайти закон розподілу функції
. Знайти закон розподілу функції 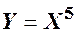 .
.
Приклад 7.8. ВВ 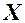 рівномірно розподілена на [1;3]. Знайти закон розподілу функції
рівномірно розподілена на [1;3]. Знайти закон розподілу функції 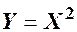 .
.
Дата публикования: 2014-11-18; Прочитано: 475 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
