Многофакторный дисперсионный анализ

Следует сразу же отметить, что принципиальной разницы между многофакторным и однофакторным ДА нет. Многофакторный анализ не меняет общую логику ДА, а лишь несколько усложняет ее, поскольку, кроме учета влияния на зависимую переменную каждого из факторов по отдельности, следует оценивать и их совместное действие. Таким образом, то новое, что вносит в анализ данных многофакторный дисперсионный анализ, касается в основном возможности оценить межфакторное взаимодействие. Тем не менее, по-прежнему остается возможность оценивать влияние каждого фактора в отдельности. В этом смысле процедура многофакторного ДА (в варианте ее компьютерного использования) несом­ненно более экономична, поскольку всего за один запуск решает сразу две задачи: оценивается влияние каждого из факторов и их взаимодействие.

Общая схема двухфакторного эксперимента, данные ко­торого обрабатываются ДА имеет вид:

Рисунок 1.1 – Схема двухфакторного эксперимента

Предположив, что в рассматриваемой задаче о каче­стве различных m партий изделия изготавливались на разных t станках и требуется выяснить, имеются ли существенные раз­личия в качестве изделий по каждому фактору:

А - партия из­делий;

B - станок.

В результате получается переход к задаче двухфакторного ДА.

Все данные представлены в таблице 1.2, в кото­рой по строкам - уровни A_i фактора А, по столбцам — уровни B_j фактора В, а в соответствующих ячейках, табли­цы находятся значения показателя качества изделий x_ijk (i=1,2,...,m; j=1,2,...,l; k=1,2,...,n).

Таблица 1.2 – Показатели качества изделий

	B1	B2	…	Bj	…	Bl
A1	x11l,…,x11k	x12l,…,x12k	…	x1jl,…,x1jk	…	x1ll,…,x1lk
A2	x21l,…,x21k	x22l,…,x22k	…	x2jl,…,x2jk	…	x2ll,…,x2lk
…	…	…	…	…	…	…
Ai	xi1l,…,xi1k	xi2l,…,xi2k	…	xijl,…,xijk	…	xjll,…,xjlk
…	…	…	…	…	…	…
Am	xm1l,…,xm1k	xm2l,…,xm2k	…	xmjl,…,xmjk	…	xmll,…,xmlk

Двухфакторная дисперсионная модель имеет вид:

x_ijk=μ+F_i+G_j+I_ij+ε_ijk, (15)

где x_ijk - значение наблюдения в ячейке ij с номером k;

μ - общая средняя;

F_i - эффект, обусловленный влиянием i-го уровня фактора А;

G_j - эффект, обусловленный влиянием j-го уровня фактора В;

I_ij - эффект, обусловленный взаимодействием двух факто­ров, т.е. отклонение от средней по наблюдениям в ячейке ij от суммы первых трех слагаемых в модели (15);

ε_ijk - возмущение, обусловленное вариацией переменной внутри отдельной ячейки.

Предполагается, что ε_ijk имеет нормальный закон распределения N(0; с²), а все математические ожидания F_*, G_*, I_i*, I_*j равны нулю.

Групповые средние находятся по формулам:

- в ячейке:

,

- по строке:

по столбцу:

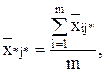
общая средняя:

В таблице 1.3 представлен общий вид вычисления значений, с помощью дисперсионного анализа.

Таблица 1.3 – Базовая таблица дисперсионного анализа

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Средние квадраты
Межгрупповая (фактор А)		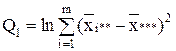m-1
Межгрупповая (фактор B)		l-1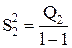
Взаимодействие		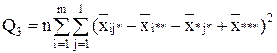(m-1)(l-1)
Остаточная		mln - ml
Общая		mln - 1

Проверка нулевых гипотез H_A, H_B, H_AB об отсутствии влияния на рассматриваемую переменную факторов А, B и их взаимодействия AB осуществляется сравнением отношен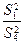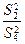ий , , (для модели I с фиксированными уровнями факторов) или отношений , , 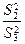(для случайной модели II) с соответствующими табличными значениями F – критерия Фишера – Снедекора. Для смешанной модели III проверка гипотез относительно факторов с фиксированными уровнями производится также как и в модели II, а факторов со случайными уровнями – как в модели I.

Если n=1, т.е. при одном наблюдении в ячейке, то не все нулевые гипотезы могут быть проверены так как выпадает компонента Q₃ из общей суммы квадратов отклонений, а с ней и средний квадрат , так как в этом случае не может быть речи о взаимодействии факторов.

С точки зрения техники вычислений для нахождения сумм квадратов Q₁, Q₂, Q₃, Q₄, Q целесообразнее ис­пользовать формулы:

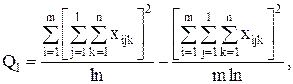
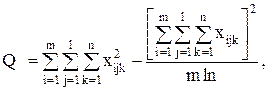
Q₃ = Q – Q₁ – Q₂ – Q₄.

Отклонение от основных предпосылок ДА— нормальности распределения исследуемой переменной и равенства дисперсий в ячейках (если оно не чрезмерное) — не сказывается существенно на результатах ДА при равном числе наблюдений в ячейках, но может быть очень чувствительно при неравном их числе. Кроме того, при нерав­ном числе наблюдений в ячейках резко возрастает сложность аппарата ДА. Поэтому рекомендуется пла­нировать схему с равным числом наблюдений в ячейках, а если встречаются недостающие данные, то возмещать их средними значениями других наблюдений в ячейках. При этом, однако, искусственно введенные недостающие данные не следует учиты­вать при подсчете числа степеней свободы.

ДА подобно t-критерию Стьюдента, позволяет оценить различия между выборочными средними; однако, в отличие от t-критерия, в нем нет ограничений на количество сравниваемых средних. Таким образом, вместо того, чтобы поставить вопрос о различии двух выборочных средних, можно оценить, различаются ли два, три, четыре, пять или k средних.

ДА позволяет иметь дело с двумя или более независимыми переменными (признаками, факторами) одновременно, оценивая не только эффект каждой из них по отдельности, но и эффекты взаимодействия между ними, поэтому позволяет проверять более сложные гипотезы.

Еще одно преимущество ДА по сравнению с обычным t-критерием для двух выборок: ДА позволяет изучать каждый фактор, управляя значениями других факторов. Это является основной причиной его большей статистической мощности (для получения значимых результатов требуется меньшие объемы выборок).

ДА определяет, есть ли эффект.

Слишком большая размерность выборок затрудняет проведение статистических анализов, поэтому имеет смысл уменьшить размер выборки.

Применив ДА можно выявить значимость влияния различных факторов на исследуемую переменную. Если влияние фактора окажется несущественным, то этот фактор можно исключить из дальнейшей обработки.

Модели ДА со случайными факторами неустойчивы к нарушениям предположений о нормальности и независимости эффектов случайных факторов. Эти нарушения могут привести к ошибкам при проверке гипотез.