 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Гражданская оборона Украины. Задания,организационное строение и порядок функционирования 2 страница
|
|
Матрица называется ленточного типа, если ненулевые элементы её располагаются параллельно главной диагонали, а остальные равны нулю.
Каждой квадратной матрице A соответствует определитель (детерминант), который обозначается detA или ∆.
Определители для матриц второго и третьего порядка вычисляются по правилу Саррюса:
∆ = detA =  =
= 
В этом случае определитель равен разности произведений элементов матрицы, расположенных вдоль главных диагоналей
Для вычисления определителя 3-го порядка к ней справа добавляются два первых столбца элементов, а затем составляется сумму произведений элементов, расположенных вдоль диагоналей, причем произведения элементов сверху вниз берутся со знаком плюс, а снизу вверх- со знаком минус.
detA =  =
= 
3.2 ДЕЙСТВИЯ С МАТРИЦАМИ
Если матрицы A и B одного типа, то имеет смысл операции сложения и вычитания.
Матрица суммы (разности), матриц A и B есть матрица C, элементы которой равны сумме (разности) соответствующих элементов матриц A и B.
Матрицу A можно умножить на число α. В результате получается матрица B, элементы которой получены умножением всех элементов матрицы A на число α.
Матрица –A=(–1)A называется противоположной матрице А. Если A-квадратичная матрица порядка n, то определитель матрицы C= αA равен:
detC = detαA = αndetA
Операция умножения матриц:
Пусть A и B матрицы типов m×n и p×q соответственно. Если число столбцов n матрицы A равно числу строк p матрицы B(n=p), то для этих матриц существует матрица C типа m×q, являются их произведением.
C =  ,
,
где  (i=1,2,…,m, j=1,2,…,q)
(i=1,2,…,m, j=1,2,…,q)
Т.е. элемент матрицы  – равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B.
– равен сумме произведений элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B.
В общем случае AB ≠ BA. Если матрица A типа m×n и B типа p×q, то AB – матрица типа m×q, а BA – p×n.
Например:
A =  ; B =
; B =  ; AB =
; AB = 
BA = 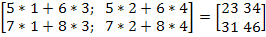 , т.е. AB ≠ BA;
, т.е. AB ≠ BA;
3.3 ОБРАТНЫЕ МАТРИЦЫ
Матрица A-1 называется обратной по отношению к квадратной матрице A, если их произведение равно единичной матрице:
AA-1= A-1*A=E;
Всякая матрица с отличным от нуля определителем имеет обратную матрицу. При этом:
detA-1= 
Минором элемента aij называется определитель (n1)-го порядка, образованный из определителя матрицы A зачеркиванием i-n строки из j-го столбца.
Алгебраическим дополнением Aij элемента aij называется его минор, взятый со знаком плюс, если сумма номеров i+j четная, и со знаком минус, если эта сумма нечетная.
Для квадратной матрицы третьего порядка после группировки слагаемых получим определитель ∆.
∆ =  =
= 
Заключенные в скобках разности произведений элементов матрицы и есть алгебраические дополнения:
Aij=(-1)i+j ×Mij
А в целом это есть разложение определителя по первой строке матрицы, т.е.:
∆ = 
Каждый элемент обратной матрицы равен отношению алгебраического дополнения  исходной матрицы A к знамению её определителя.
исходной матрицы A к знамению её определителя.
Таким образом, если detA = ∆ для этой же матрицы
 =
=  =
=  =E
=E
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
ЗАДАНИЕ 2
ДЕЙСТВИЯ С МАТРИЦАМИ
1) Вычислить произведение матриц A и B.
2) Найти матрицу  обратную матрице A.
обратную матрице A.
Задания приведены в таблице 2.
ТАБЛИЦА 2
| 0,1,2 | 3,4,5,6 | 7,8,9 | ||||
| A | B | A | B | A | B | |
| 5 8 1 1 2 3 2 –3 2 | –1 0 5 0 1 3 2 –2 5 | 1 2 1 3 –5 3 2 7 –1 | 1 2 1 2 3 1 2 1 3 | 1 2 1 2 3 1 2 1 3 | 0 –2 6 2 4 3 0 –3 4 | |
| 1 2 4 5 1 2 3 –1 1 | 0 2 3 1 0 –2 3 1 1 | 4 –3 2 2 5 –3 5 6 –2 | 2 3 1 4 –1 0 0 1 2 | 2 –1 –1 5 4 –2 3 –2 4 | 5 1 2 –1 2 0 1 0 1 | |
| 5 3 –1 2 0 4 3 5 –1 | 1 1 2 2 –1 2 4 1 4 | 3 –1 0 –2 1 1 2 –1 4 | –1 2 4 0 3 2 –1 –3 4 | 3 –1 1 2 –5 –3 1 1 –1 | 1 4 2 2 1 –2 0 1 –1 | |
| 1 1 1 2 –1 –5 3 –2 0 | 4 2 1 3 –2 0 0 –1 2 | 2 1 –1 1 1 1 3 –1 1 | 1 0 3 –2 0 1 –1 2 1 | 2–1–3 3 4–5 0 2 7 | 2 3 1 –1 2 4 5 3 1 | |
| 1 5 1 2 –1 –1 1 –2 –1 | –1 –2 3 2 3 5 1 4 –1 | 1 –2 3 2 3 –4 3 –2 –5 | 2 3 1 4 –1 0 0 1 2 | 3 4 2 2 –1 –3 1 5 1 | 2 1 3 1 –2 0 4 –3 0 |
Вычислить сумму произведений одноименных элементов, аналогично рассчитывая остальные сij.
С11= 
С12= 
С13 = 
С21= 
С22= 
С23= 
С31= 
С32= 
С33= 
Следовательно:
С=A*B= 
2. Найдем обратную матрицу A-1. Матрица
A=  имеет обратную, если её определитель ∆ не равен нулю.
имеет обратную, если её определитель ∆ не равен нулю.
Вычислить определитель.
Для этого разложим его по первой строке матрицы A
∆= 
Вычислим алгебраические дополнения по формуле:

Минор  получают вычеркиванием i-й строки и j-го столбца матрицы A, и из оставшейся части матрицы рассчитывается определитель:
получают вычеркиванием i-й строки и j-го столбца матрицы A, и из оставшейся части матрицы рассчитывается определитель:
 =(-1)1+1
=(-1)1+1 
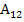 =(-1)1+2
=(-1)1+2 
 =(-1)1+3
=(-1)1+3 
Определитель ∆= 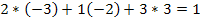 не равен 0, значит, матрица A имеет обратную матрицу A-1.
не равен 0, значит, матрица A имеет обратную матрицу A-1.
Выражение обратной матрицы:

Здесь  - алгебраическое дополнение элементов
- алгебраическое дополнение элементов 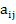 матрицы A.
матрицы A.
Так как 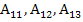 уже вычислены, то вычислим остальные
уже вычислены, то вычислим остальные  :
:
 =(-1)2+1
=(-1)2+1 
 =(-1)2+2
=(-1)2+2 
Подставим  в выражение для
в выражение для  ,
,
 =(-1)2+3
=(-1)2+3 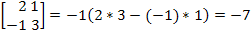
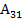 =(-1)3+1
=(-1)3+1 
 =(-1)3+2
=(-1)3+2 
 =(-1)3+3
=(-1)3+3 
получим обратную матрицу:

Для матрицы A и её обратной должно выполняться равенство  , где E- единичная матрица.
, где E- единичная матрица.
Перемножим матрицы A и 

Обратная матрица определена верно.
3.4 РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
МЕТОДОМ ИСКЛЮЧЕНИЯ ГАУССА.
Метод основан на приведении матрицы системы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Сначала с помощью первого уравнения исключается х1 из всех последующих уравнений. Затем с помощью второго уравнения исключается х2 из третьего и всех последующих уравнений. Этот процесс, называемый прямым ходом метода Гаусса, продолжается до тех пор, пока в левой части последнего (n-ого) уравнения не останется лишь один член с неизвестным xn, т.е. матрица системы будет приведена к треугольному виду.
Обратный ход метода Гаусса состоит в последовательном вычислении искомых неизвестных: решая последнее уравнение, находим единственное в этом уравнении неизвестное xn. Далее, используя это значение из предыдущего уравнения, вычисляем xn-1 и т.д. Последним найдем x1 из первого уравнения.
ВЫПОЛНИТЬ САМОСТОЯТЕЛЬНО
ЗАДАНИЕ 3
РЕШИТЬ СИСТЕМУ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ
ИСКЛЮЧЕНИЯ ГАУССА.
Система задана в таблице 3.
ТАБЛИЦА 3
| 0,1,2 | 3,4,5,6 | 7,8,9 | |
| 0, | x1+x2+2x3+3x4=1 3x1–x2–x3–2x4=–4 2x1+3x2–x3–x4=–6 x1+2x2+3x3–x4=–4 | x1+2x2+3x3+4x4=5 2x1+x2+2x3+3x4=1 3x1+2x2+x3+2x4=1 4x1+3x2+2x3+x4=–5 | 2x1–x2+3x3–2x4=4 3x1+3x2+3x3+2x4=6 3x1–x2–x3+2x4=6 3x1–x2+3x3–x4=6 |
| 2, | x1+2x2+3x3–2x4=6 x1–x2–x3–3x4=8 3x1+2x2–x3+2x4=4 2x1–3x2+3x3+x4=–8 | x1+3x2+5x3+7x4=12 3x1+5x2+7x3+x4=0 5x1+7x2+x3+3x4=4 7x1+x2+3x3+5x4=16 | 2x1–6x2+2x3+2x4=12 x1+3x2+5x3+7x4=12 3x1+5x2+7x3+x4=0 5x1+7x2+x3+3x4=4 |
| 4, | 5x1–x2+x3+3x4=–4 x1+2x2+3x3–2x4=6 2x1–x2–2x3–3x4=8 3x1+2x2–x3+2x4=4 | 4x1–2x2+x3+4x4=3 2x1–x2+x3+3x4=1 3x1–x3+2x4=–3 2x1+2x2+2x3+3x4=–6 | –x1+x2+x3+x4=4 2x1+x2+2x3+3x4=1 3x1+2x2+x3+2x4=1 4x1+3x2+2x3+x4=–5 |
| 6, | 2x1–x2+2x3+2x4=–3 3x1+2x2+x3–x4=3 x1–3x2–x3–3x4=0 4x1+2x2+2x3+54=–15 | x1–2x2+3x3–4x4=–2 2x1+3x2+4x3–5x4=8 3x1–x2–x3+7x4=–2 2x1–x2+6x3–3x4=7 | 3x1+2x2+5x3–x4=3 2x1–3x2–3x3+4x4=1 4x1+x2+3x3+2x4=3 5x1–2x2+x3+3x4=5 |
| 8, | 2x1–x2+5x3–x4=1 3x1–3x2–2x3–5x4=2 x1–x2+2x3+3x4=10 3x1+2x2+7x3–2x4=1 | 3x1+x2+2x3–x4=8 2x1–3x2–3x3+x4=–3 4x1+2x2+5x3+3x4=6 x1+2x2–4x3–3x4=–3 | 2x1+3x2+5x3+x4=6 3x1+x2–x3+5x4=0 2x1–x2+3x4=–5 2x1+2x2–x3+7x4=–3 |
ПРИМЕР: Решить систему методом Гаусса
2x1+x2–0,1x3+x4=2,7
0,4x1+0,5x2+4x3–8,5x4=21,9
0,3x1–x2+x3 + 5,2x4=–3,9
x1+0,2x2+2,5x3–x4=9,9
РЕШЕНИЕ: Прямой ход. Приведем систему к треугольному виду. Исключим х1 из второго, третьего и четвертого уравнения. Для этого разделим первое уравнение на 2, получим систему:
| x1+0,5x2–0,05x3+0,5x4=1,35 0,4x1+0,5x2+4x3–8,5x4=21,9 0,3x1–x2+x3 + 5,2x4=–3,9 x1+0,2x2+2,5x3–x4=9,9 |
Затем умножим первое уравнение на 0,4 и результат вычтем из второго, затем умножим на 0,3 и вычтем из третьего, затем первое уравнение вычтем из четвертого. Получим систему:
| x1+0,5x2–0,05x3+0,5x4=1,35 0,3x2+4,02x3–8,7x4=21,36 –1,15x2+1,015x3 + 5,05x4=–4,305 –0,3x2+2,55x3–1,5x4=8,55 |
Первое уравнение исключим из полученной системы и оставим его в качестве первого уравнения треугольной системы. Получим систему:
| 0,3x2+4,02x3–8,7x4=21,36 –1,15x2+1,015x3 + 5,05x4=–4,305 –0,3x2+2,55x3–1,5x4=8,55 |
Первое уравнение разделим на 0,3 и получим систему:
| x2+13,4x3–29x4=71,2 –1,15x2+1,015x3 + 5,05x4=–4,305 –0,3x2+2,55x3–1,5x4=8,55 |
Исключим х2 из второго и третьего уравнений по аналогии с предыдущим. Получим систему:
| x2+13,4x3–29x4=71,2 16,425x3 – 28,3x4=77,575 6,57x3–10,2x4=29,910 |
Первое уравнение исключаем из системы и оставляем его в качестве второго уравнения треугольной системы. Получим систему:
| 16,425x3 – 28,3x4=77,575 6,57x3–10,2x4=29,910 |
Первое уравнение разделим на 16,425 и исключим х3 из второго уравнения:
| x3 – 1,72298x4=4,72298 1,11998x4=–1,11998 |
Первое уравнение полученной системы берем в качестве третьего уравнения треугольной системы, а второе уравнение – в качестве четвертого уравнения треугольной системы.
Таким образом получим треугольную систему:
| x1+0,5x2–0,05x3+0,5x4=1,35 x2+13,4x3–29x4=71,2 x3 – 1,72298x4=4,72298 1,11998x4=–1,11998 |
Обратный ход. Из треугольной системы находим:
х4=–1; х3=3; х2=2; х1=1.
4. ПРИБЛИЖЕНИЕ ФУНКЦИИ. ИНТЕРПОЛЯЦИЯ.
Процесс приближения функции находит широкое распространение не только в научной и технической областях деятельности человека, но и в его повседневной деятельности. Одним из видов приближения функции является интерполяция. Поэтому каждому студенту необходимо быть знакомым с основными методами и приемами интерполирования.
4.1 ПОСТАНОВКА ЗАДАЧИ ПРИБЛИЖЕНИЯ ФУНКЦИИ.
Пусть на отрезке [a,b] заданы точки х0,х1,…,хn и значения некоторой функции f(x) в этих точках f(x0)=y0, f(x1)=y1,…,f(xn)=yn.
| Необходимо построить такую функцию F(x), которая принимает в точках xi (i=0,1,2,…,n) значения, равные значениям f(xi): F(x0)=y0, F(x1)=y1, …, F(xn)=yn Такая функция F(x) называется интерполирующей, а точки x0, x1, …, xn – узлами интерполяции. |
Интерполяционную функцию F(x) используют для вычисления значений функции f(x) в промежутках между точками xi, xi+1.
Процесс вычисления f(x) в промежуточных точках между x0,xn называется интерполяцией.
Наиболее часто встречается интерполяция многочленами
Fn(x) = a0 + a1x + a2x2 + … +anxn
Для вывода формулы многочлена Pn(x) по заданным параметрам функции f(x) прежде всего введем понятие конечные разности функции.
4.2 КОНЕЧНЫЕ РАЗНОСТИ РАЗЛИЧНЫХ ПОРЯДКОВ.
Рассмотрим случай равноотстоящих значений аргументов, т.е.
xi – xi-1 = h = const (i=1,2,…,n)
Величина h называется шагом.
Пусть известны значения функции в узлах xi
yi = f(xi)
Составим разности значений функции:
∆y0 = y1 – y0 = f(x0 + h) – f(x0)
∆y1 = y2 – y1 = f(x0 + 2h) – f(x0 + h)
… … … … … … … …
∆yn-1 = yn – yn-1 = f(x0 + nh) – f(x0 + (n-1)h)
Эти значения называются первыми конечными разностями (или разностями первого порядка) функции. Аналогично составляются конечные разности второго порядка:
∆2y0 = ∆(∆y0) = ∆y1 - ∆y0; ∆2y1 = ∆(∆y1) = ∆y2 - ∆y1
Аналогично конечной разностью k-ого порядка будет:
∆kyi = ∆k-1yi+1 - ∆k-1yi; i=0,1,…,n–1
Конечные разности различных порядков удобно располагать в виде горизонтальной таблицы разностей.
Используя эти формулы, построим горизонтальную таблицу конечных разностей для n=5.
| x | y | ∆y | ∆2y | ∆3y | ∆4y |
| x0 x1 x2 x3 x4 | y0 y1 y2 y3 y4 | ∆y0 ∆y1 ∆y2 ∆y3 | ∆2y0 ∆2y1 ∆2y2 | ∆3y0 ∆3y1 | ∆4y0 |
Пример 3. Составить горизонтальную таблицу разностей функции
y = 2x3 – 2x2 + 3x – 1
от начального значения x0 = 0, приняв шаг h = 1.
РЕШЕНИЕ: Полагая x0=0, x1=1, x2=2, x3=3, находим соответствующие значения
y0=–1, y1=2, y2=13, y3=44
Эти значения запишем в таблицу:
| Отсюда имеем ∆y0 = y1 – y0 = 3 ∆y1 = y2 – y1 = 11 ∆y2 = y3 – y2 = 31 ∆2y0 = ∆y1 - ∆y0 = 8 ∆2y1 = ∆y2 - ∆y1 = 20 ∆3y0 = ∆2y1 - ∆2y0 = 12 |
Рассматривая символ ∆ как оператор, можно указать следующие его свойства:
∆(u + v) = ∆u + ∆v
∆(C∙u) = C∆u
∆m(∆nu) = ∆m+nu
∆0(u) = u
Конечные разности можно выразить непосредственно через значения функции
∆y0 = y1 – y0
∆2y0 = ∆y1 - ∆y0 = (y2 – y1) – (y1 – y0) = y2 – 2y1 + y0
∆3y0 = ∆2y1 - ∆2y0 = (∆y2 - ∆y1) – (∆y1 - ∆y0) = ∆y2 – 2∆y1 + ∆y0 = (y3 – y2) – 2(y2 – y1) + (y1 – –y0) = y3 – 3y2 + 3y1 – y0
Аналогично для любого k в узле x0 можно написать
∆ky0 = yk – kyk-1 + 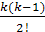 yk-2 + … + (–1)ky0 (4.1)
yk-2 + … + (–1)ky0 (4.1)
Эту формулу можно записать и для значения разности в узле xi:
∆kyi = yk+1 – kyk+i-1 + 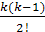 yk+i-2 + … + (–1)kyi
yk+i-2 + … + (–1)kyi
4.3 ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА.
Перейдем к построению интерполяционного многочлена Ньютона. Этот многочлен будем искать в следующем виде:
N(x) = a0 + a1(x – x0) + a2(x – x0)(x – x1)+ … + an(x – x0)(x – x1)…(x – xn-1) (4.2)
График многочлена должен проходить через заданные узлы, т.е. N(xi) = yi (i=0,1,2,…n). Эти условия используем для нахождения коэффициентов многочлена; учитывая, что xi – xi-1=h:
N(x0) = a0 = y0
N(x1) = a0 + a1(x1 – x0) = a0 + a1h = y1
N(x2) = a0 + a1(x2 – x0) + a2(x2 – x0)(x2 – x1) = a0 + a1h + 2a2h2 = y2
.... … … … … … …
Отсюда найдем коэффициенты:
a0 = y0; a1 = 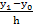 =
= 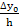 ;
;
a2 = 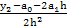 =
= 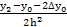 =
= 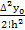
Дата публикования: 2014-11-18; Прочитано: 285 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
