Вращение вокруг осей, перпендикулярных к плоскости проекций

Вращение точки. Будем поворачивать точку А вокруг оси, перпендикулярной к плоскости (рис.1). Ось вращения - i. Рассмотрим траектории, описываемые проекциями точки при ее вращении. На плоскости горизонтальная проекция точки А – А₁ будет двигаться по дуге окружности радиуса, равного расстоянию от оси О₁ до А₁. На плоскости фронтальная проекция точки А₂ будет перемещаться по прямой, параллельной оси проекций, так как окружность лежит в плоскости ║ и .

Если ось вращения перпендикулярна (рис.2), то фронтальная проекция точки будет двигаться по дуге окружности, а горизонтальная по прямой, параллельной оси проекций. Эпюры вращения точки А показаны на рис. 3.

Вращение отрезка. Пусть задан отрезок [АВ] и ось вращения ί, перпендикулярная плоскости .

Для того, чтобы построить проекции отрезка, повернутого вокруг оси ί на угол φ, достаточно определить новое положение двух его точек, например А и В. При построении горизонтальных проекций было выполнено условие < А ₁ ί ₁ =< В ₁ ί ₁ 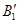Фронтальные проекции точек А и В перемещаются по горизонтальным прямым, перпендикулярным линиям проекционной связи. Они определены пересечением этих прямых с линиями связи, проведенными через точки и 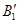. Заметим, что ΔА₁ ί ₁ В₁=Δ ί ₁ 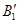(по двум сторонам и заключенному между ними углу), поэтому конгруэнтны и высоты треугольников, т.е. ί ₁ С₁= ί ₁ 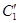. Используя это равенство, тот же поворот отрезка АВ можно осуществить следующим образом:

1. Из точки ί ₁ опустить перпендикуляр ί ₁С₁ на А₁В₁;

2. Этот перпендикуляр повернуть на угол φ в заданном направлении в положение ί ₁ ;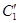

3. Через точку 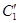провести прямую перпендикулярную ί ₁ ;

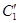4. При пересечении построенной прямой дугами радиусов ί ₁А₁ и ί ₁В₁ получить точки и .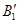

5. Построить фронтальные проекции и .

При вращении геометрической фигуры вокруг оси, перпендикулярной плоскости проекций, одна из проекций формы (на плоскости оси вращения) не изменяется.

Задача 1. Определить истинную величину отрезка АВ и угол наклона его к плоскости .

Для решения необходимо поставить отрезок в положение параллельное плоскости проекций . Этого можно достичь, если повернуть отрезок вокруг оси так, чтобы горизонтальная проекция отрезка заняла положение параллельное оси ОХ (рис.5).

Задача 2. Преобразовать чертеж так, чтобы прямая общего положения в результате вращения стала проецирующей (рис. 6).

Достигается это двойным поворотом прямой вокруг двух различных осей:

1. Поворачиваем отрезок [AB] до положения, параллельного [ 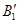]║ОХ.

2. Поворачиваем отрезок [AB] до положения, перпендикулярного [ 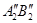] ОХ.

Задача 3. Вращением вокруг оси, перпендикулярной к , переместить точку А на прямую (рис.7). Горизонтальная проекция точки А – А₁ перемещаясь по направлению, параллельному оси ОХ, перемещается с горизонтальной проекцией прямой а в точке . в проекционном соответствии на проекции а ₂ . [А₁ ] делим пополам и получим горизонтальную проекцию оси вращения i₁. i₂ получим в проекционном соответствии на отрезок [А₁ ].

Задача 4. Повернуть точку А вокруг оси i до совпадения с плоскостью тождества (рис.8). При вращении точки вокруг оси i фронтальная проекция точки А перемещается по направлению, параллельному оси ОХ, а горизонтальная по дуге радиуса [ i₁ А₁]. Пересечение прямой и дуги определяет проекция = .

ВРАЩЕНИЕ ПЛОСКОСТИ.

Для того, чтобы повернуть плоскость, достаточно повернуть две ее точки. Новое положение плоскости будет определяться повернутыми точками и неподвижной точкой пересечения плоскости с осью вращения (рис.9).