Сумматоры. Меняющиеся во времени параллельные двоичные коды удобно рассматривать как совокупность несвязанных между собой логических переменных — каждый разряд кода своя

Меняющиеся во времени параллельные двоичные коды удобно рассматривать как совокупность несвязанных между собой логических переменных — каждый разряд кода своя переменная. При этом оказывается возможным применить логические устройства для разнообразной обработки кода.

Рассмотрим, например устройство, преобразующее одноразрядные коды слагаемых в коды двоичной суммы и переноса. Такое устройство называют полусумматором.

Его таблица истинности имеет вид:

A	B	C	S
↑операнды↑	↑перенос	↑сумма

A, B — операнды;

S — сумма;

C — перенос.

Полусумматор строится из элементов “исключающее ИЛИ” и И по следующей схеме:

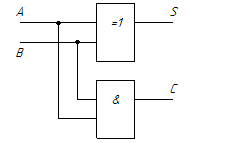
На функциональных схемах полусумматор изображают следующим образом:

Полусумматор не позволяет учитывать перенос, возникающий при суммировании младших разрядов, и поэтому не пригоден для суммирования многоразрядных кодов.

Такой перенос учитывает полный сумматор, построенный с помощью двух полусумматоров и элемента ИЛИ. Функциональная схема полного сумматора имеет вид:

Таблица истинности полного сумматора и его условное обозначение выглядят следующим образом:

A0	B0	C0	C1	S0

Одноразрядные полные сумматоры можно соединить друг-с-другом, обеспечивая суммирование многоразрядных кодов. Например, функциональная схема двухразрядного сумматора имеет вид:

На функциональной схеме рассмотренная структура обозначается следующим образом:

Цепи переноса многоразрядных комбинационных сумматоров содержат много последовательно включенных логических элементов. Это ограничивает быстродействие сумматора. Поэтому иногда сумматор снабжают дополнительным блоком параллельного (ускоренного) переноса.