Формулы численного интегрирования. Формулы прямоугольников и трапеций

Численное интегрирование (историческое название: (численная) квадратура) — вычисление значения определённого интеграла(как правило, приближённое). Под численным интегрированием понимают набор численных методов отыскания значения определённого интеграла.

Численное интегрирование применяется, когда:1. Сама подынтегральная функция не задана аналитически. Например, она представлена в виде таблицы (массива) значений в узлах некоторой расчётной сетки. 2. Аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции. Например, f(x) = exp(− x²).

В этих двух случаях невозможно вычисление интеграла по формуле Ньютона-Лейбница. Также возможна ситуация, когда вид первообразной настолько сложен, что быстрее вычислить значение интеграла численным методом.

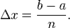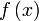Формулы прямоугольников Пусть требуется определить значение интеграла функции на отрезке . Этот отрезок делится точками на равных отрезков длиной Обозначим через значение функции в точках 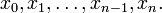Далее составляем суммы Каждая из сумм — интегральная сумма для 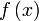на и поэтому приближённо выражает интеграл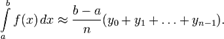

Если заданная функция — положительная и возрастающая, то эта формула выражает площадь ступенчатой фигуры, составленной из «входящих» прямоугольников, также называемая формулой левых прямоугольников, а формула

выражает площадь ступенчатой фигуры, состоящей из «выходящих» прямоугольников, также называемая формулой правых прямоугольников. Чем меньше длина отрезков, на которые делится отрезок , тем точнее значение, вычисляемое по этой формуле, искомого интеграла.

Очевидно, стоит рассчитывать на бо́льшую точность если брать в качестве опорной точки для нахождения высоты точку посередине промежутка. В результате получаем формулу средних прямоугольников: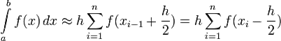

где Учитывая априорно бо́льшую точность последней формулы при том же объеме и характере вычислений её называют формулой прямоугольников

Метод трапеций

Если функцию на каждом из частичных отрезков аппроксимировать прямой, проходящей через конечные значения, то получим метод трапеций.

Площадь трапеции на каждом отрезке: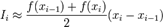

Погрешность аппроксимации на каждом отрезке:

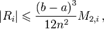где 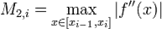Полная формула трапеций в случае деления всего промежутка интегрирования на отрезки одинаковой длины h:

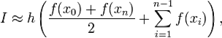где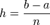

Погрешность формулы трапеций: 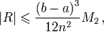где