Лінійний елемент поверхні еліпсоїда

Через дану точку на поверхні еліпсоїда можна провести низку різних ліній. Кожна з цих ліній певним чином зорієнтована відносно однієї з координатних ліній, а саме меридіана. Кут орієнтування, тобто кут між дотичними, проведеними до меридіана в північному напрямі та заданою лінією, називається геодезичним азимутом А. Він відраховується від меридіана в сторону руху годинникової стрілки. Один і той азимут може мати і декілька різних ліній. Це буде в тому випадку, коли ці лінії мають спільну дотичну в даній точці., наприклад, паралель і перший вертикал в заданій точці поверхні еліпсоїда мають однаковий азимут, який дорівнює 90⁰ (або 270⁰), хоча розташовані вони в різних площинах.

Диференціал дуги ds довільної кривої на поверхні еліпсоїда називається лінійним елементом поверхні еліпсоїда.

На поверхні еліпсоїда координатні лінії мають своє позначення: Х – довжина дуги меридіана від екватора (в сторону полюса) до даної точки; Y – довжина дуги паралелі від середнього (початкового) меридіана до даної точки.

Відомо, що для будь-якої кривої радіус її кривини в даній точці дорівнює відношенню диференціала дуги кривої до до диференціалу кута між дотичними до кривої в крайніх точках цієї дуги. Якщо позначити диференціал дуги меридіана через , а паралелі через , диференціал кута між дотичними до крайніх точок елемента дуги меридіана через , а паралелі через , то, згідно вище зазначеного, для диференціалів дуг меридіана та паралелі отримаємо відповідно

Спроектувавши лінійний елемент на координатні лінії (лінії меридіанів та паралелей), отримаємо (див. рис 2.8)

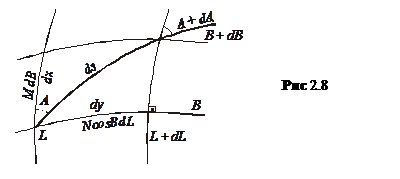(2.45)

Звідки,

(2.46)

Отримане рівняння (2.46) є аналогом рівняння (1.4) для поверхні еліпсоїда обертання, тобто є першою квадратичною формою поверхні еліпсоїда.

Характер зміни довготи та широти при переміщенні вздовж будь-якої лінії на поверхні еліпсоїда, може бути виражений наступними диференціальними рівняннями, що випливають із (2.45)

(2.47)

(2.48)

Серед цих формул відсутній вираз, що характеризує зміну азимута А в залежності від переміщення вздовж лінії на величину ds. Справа в тому, що ця залежність не буде однаковою для всіх ліній, тоді як приведенні вище формули відносяться до будь-якої лінії на поверхні.

2.6. Довжини дуг меридіана та паралелі. Площа сфероїдної трапеції.

Поскільки у формулі лінійного елемента поверхні еліпсоїда (2.46) кожна складова в правій частині є квадрат диференціала дуги координатної лінії, то звідти отримаємо наступні вирази для довжин дуг меридіана та паралелі:

Рис. 2.9

На практиці також часто виникає необхідність обчислення площі частин поверхні еліпсоїда (сфероїдних трапецій), які представляють площі знімальних трапецій.

Сфероїдною трапецією називається частина поверхні еліпсоїда, обмежена меридіанами і паралелями (рис 2.10).

		Елемент площі сфероїдної трапеції dP визначається добутком диференціалів дуг координатних ліній: dP=dXdY. Замінивши dX і dY їх значеннями за формулами (2.45) отримає-мо

Рис. 2.10

де М і N визначаються формулами (2.39) і (2.40) відповідно.

Тоді площа сфероїдної трапеції визначається подвійним інтегралом:

(2.50)