Прогнозирование в рядах динамики

Основой прогнозирования является предположение, что закономерность, действующая внутри анализируемого ряда динамики, сохраняется и в дальнейшем. Точность прогноза зависит того, насколько обоснованными окажутся предположения о сохранении на будущее действий факторов, сформировавших в ряду динамики его компоненты.

Установление сроков прогнозирования зависит от задачи исследования. Чем короче сроки упреждения, тем надежнее результаты прогноза.

При прогнозировании выбор методов зависит от характера изменений в базисном ряду динамики и поставленной задачи исследования.

1. При прогнозировании на базе ряда динамики с постоянными абсолютными приростами 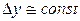(на базе абсолютных приростов) применяем формулу

,

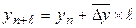где 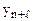– экстраполируемый уровень; 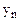– конечный уровень ряда; 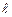– срок прогноза.

2. При прогнозировании на базе ряда со стабильными темпами роста 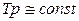(на базе темпов роста) применяется формула .

3. При прогнозировании тренда на основе модели аналитического выравнивания применяется трендовая модель .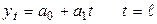

Прогнозируемые уровни задаются вероятностями (p) принадлежности интервалу. Для границ интервалов используется формула 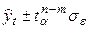, где 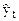– точечный прогноз, рассчитанный по модели; 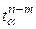– коэффициент доверия распределения Стьюдента, при уровне значимости a=1-p и степенях свободы n-m (Например при 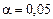(р=95%) и n-m=8 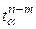= 2.306). Остаточное среднеквадратическое отклонение тренда, скорректированное по числу степеней свободы (n – m)

,

где n – число уровней базисного ряда динамики: m – число параметров модели.

Пример 1. Имеются данные о продаже легковых автомобилей.

T
У

Определить показатели динамики продаж от года к году (относительные показатели) и средние за весь анализируемый период.

Решение. Расчет показателей динамики

Наименование показателя	Годы
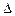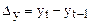
1. Абсолют. прирост, , тыс. шт.	с переменной базой	–	810-788	867-810	1054-867
с постоянной базой	–	810-788	867-788	1054-788
2. Коэффициент роста, Кр	с переменной базой
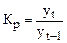
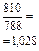
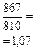
с постоянной базой
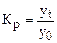
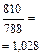
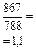
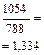
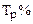
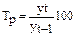
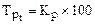
3. Темп роста	с переменной базой		102,8		121,2
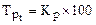
с постоянной базой		102,8		133,4
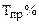
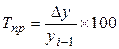
4. Темп прироста,	с переменной базой	–	102,8-100 =2,8		21,2
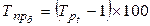
с постоянной базой	–	2,8		33,4
5. Абсолютное значение 1% прироста, А, тыс. шт.	с переменной базой	–

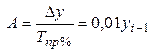
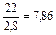
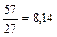
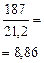
Средний уровень интервального ряда динамики

тыс. шт.

Средний абсолютный прирост

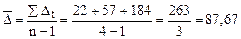тыс. шт.,

или 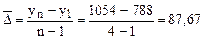тыс. шт.

Средний коэффициент роста ,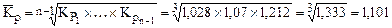

Или .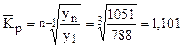

Средний темп роста .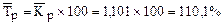

Средний темп прироста ,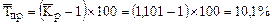

Или .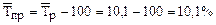

Средняя величина абсолютного значения 1% прироста

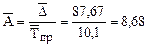тыс. шт.

Пример 2. По данным о розничном товарообороте нужно провести анализ основной тенденции развития товарооборота (млрд. руб.)

Год	Объем розничн. товарооб., у	Темп роста, %	Абсолютный прирост, млрд. руб.	ti	ti2	tiyi
	11,18 12,23 13,28 14,31 15,36 16,40	– 109,4 108,6 107,7 107,3 106,8	– 1,05 1,05 1,03 1,05 1,04			11,18 24,46 39,84 57,24 76,80 98,40	11,183 12,226 13,269 14,312 15,355 16,398
В сред.	14,32	107,9	1,04			307,92	82,743
	82,76

Развитие товарооборота происходило с затухающими темпами роста и относительно стабильными абсолютными приростами.

Для установления типа развития определяющим признаком является характер изменения абсолютных приростов, так как при среднем абсолютном приросте 1,04 млрд. руб. величина их изменений незначительна . Ряд можно считать с равномерным развитием, поэтому можно применить функцию 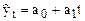. Расчеты сведем в таблицу и определим коэффициенты уравнения выравнивания.

млрд. руб.

млрд. руб.

Составим трендовую модель динамического ряда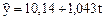

Параметр 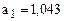показывает, что объем возрастал в среднем на 1,043 млрд. руб. в год.

На основе полученной модели определим теоретические уровни и среднее квадратическое отклонение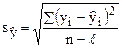

Пример 3. На основе следующих отчетных данных по грузовому автотранспорту рассчитать интервальный прогноз перевозок на 1998 г. с вероятностью 0,99

t
у

Решение. Все вспомогательные расчеты выполним в таблице

Год	Объем, тыс. т у	Первые разн.	t	t2	Yt	Теор. уров.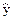
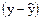
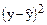
		–	-7 -5 -3 -1		-2520 -1905 -1203 -422	359,7 380,5 401,3 422,1 442,9 463,7 484,5 505,3		0,09 0,25 0,09 0.01 0,01 0.49 0,25 0,09
Итого								1,28

Первые разности приблизительно равны между собой, поэтому для выравнивания берем линейную модель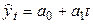

Для нахождения 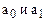используется система нормальных уравнений

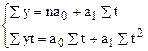
Для упрощения системы показатели времени t обозначим так, чтобы 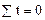(способ отсчета от условного нуля), тогда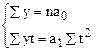

Вычислим параметры уравнения

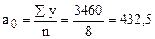тыс. т., 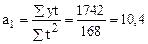тыс. т.

Составим модель динамического ряда (тренда) . Вычислим теоретические уровни ряда по полученной модели и точечный прогноз для 1998 г.

тыс. т

Определим среднее квадратическое отклонение для полученной модели динамического ряда

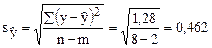тыс. т

Коэффициент доверия 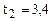при вероятности р = 0,99, уровню значимости 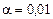и числе степеней свободы .

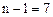Интервальный прогноз для 1998 г.

Y₉= .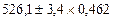

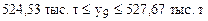
Прогнозирование на основе постоянного абсолютного прироста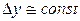

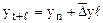
Определим средний абсолютный прирост тыс. т

Для 1998 г. значение 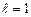Прогноз на 1998 г. 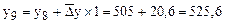тыс. т