Вычисление коэффициента инбридинга

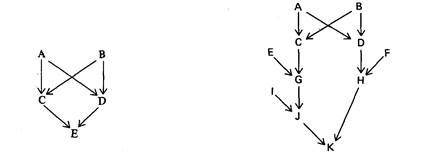
Определим значение коэффициента инбридинга F в потомстве сибсов, т.е. особей, имеющих одного и того же отца и одну и ту же мать, другими словами, родных братьев и сестер. На рис. 25.1 изображена схема скрещивания, или родословная, для этого случая; каждая стрелка соответствует передаче следующему поколению одной гаметы. Пусть А и В - не состоящие в родстве родители, из гамет которых образуются зиготы С и D. Зигота E возникает при слиянии гамет от С и D, т.е. от сибсов. Поскольку А и В не состояли в родстве, можно считать, что их аллели в определенном локусе не идентичны по происхождению. Эти аллели у особи А можно обозначить а₁а₂, а у особи Β - а₃а₄ (различные индексы указывают лишь, что аллели не являются идентичными по происхождению, хотя и могут быть идентичными по структуре). Вероятности появления четырех типов потомков от скрещивания А х В составляют 1/4 (а₁а₃), 1/4 (a₁a₄), 1/4 (а₂а₃) и 1/4 (а₂а₄). Нам нужно определить вероятность того, что в потомстве от скрещивания сибсов появятся особи, гомозиготные по какому-нибудь одному аллелю, т.е. а₁а₁ или а₂а₂, или а₃а₃, или а₄а₄. Эта вероятность равна 1/4.

Родитель А производит гаметы двух типов a₁ и а₂, причем каждую с вероятностью 1/2. Следовательно, вероятность того, что С получит от А а₁ равна 1/2 и вероятность того, что С передаст этот аллель (если он имеет его) своему потомку Е, также равна 1/2. Таким образом, вероятность того, что Ε получит аллель а ₁от А через С, равна 1/2·1/2= 1/4. Вероятность того, что от А аллель a_t перейдет к D, а от D к Е, также равна 1/2 · 1/2 = 1/4. В результате Е получит аллель α ₁с вероятностью

Рис. 25.1. Родословная потомства от скрещивания между братом и сестрой.	Рис. 25.2. Родословная потомства от скрещивания между двоюродными дядей (теткой) и племянницей (племянником).