Проверка адекватности модели. Для проверки гипотезы адекватности модели необходимо сравнить две суммы квадратов:

Для проверки гипотезы адекватности модели необходимо сравнить две суммы квадратов:

1) Остаточную сумму квадратов, характеризующую отклонение от регрессии

2) Сумму квадратов, обусловленную регрессией

где .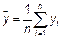

Тогда выборочное значение F, имеющее распределение Фишера

может служить проверкой адекватности для заданного уровня значимости l (обычно для экономических задач l=0,05) и степеней свободы f ₁= ; f ₂= , где 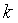– число оцениваемых параметров, исключая свободный коэффициент.

Если F ³ F _{l; f1; f2} – модель адекватна (прил.1). Остаточную дисперсию ошибки

можно использовать в качестве оценки дисперсии – дисперсии случайной величины. Результаты проверки адекватности удобно представить в виде таблицы (табл. 1).

Полезной характеристикой линейной регрессии является коэффициент детерминации, вычисляемый по формуле

Т а б л и ц а 1

Источник изменения	Сумма квадратов	Число степеней свободы	Оценка дисперсии
Модель
Ошибка
Сумма

Коэффициент детерминации равен той доле результатов наблюдений относительно горизонтальной прямой , которая объясняется уравнением регрессии. Величина является оценкой множественного коэффициента корреляции между результатами наблюдений и вычисленными значениями . Если R ²=0.75 это значит, что модель работает на 75%, а 25% приходится на ошибку или неучтенные в модели факторы (для практических целей целесообразно, чтобы R ² ³ 0,75). Для небольших значений n <30 необходимо использовать скорректированный коэффициент детерминации