Регрессионный анализ. В регрессионном анализе изучается связь и определяется количественная зависимость между зависимой переменной и одной или несколькими независимыми

В регрессионном анализе изучается связь и определяется количественная зависимость между зависимой переменной и одной или несколькими независимыми переменными.

При решении многих инженерных задач возникает необходи­мость в установлении связи между k независимыми переменными х₁, x₂,..., x_k и зависящей от них величиной у. Между переменными величинами возможны следующие типы связей.

1. Функциональная связь между неслучайными величинами. В этом случае зависимая переменная у вполне определенно задает­ся независимыми переменными x₁, х₂, …, х_к.

2. Функциональная связь между случайными величинами.

3.Стохастическая связь между случайными величинами. Стоха­стическая связь проявляется в том, что одна из случайных вели­чин реагирует на изменения другой изменениями своего закона распределения. Наиболее простым видом стохастической связи является корреляционная связь. Корреляционная связь между дву­мя случайными величинами выражается в том, что на изменения одной случайной величины другая случайная величина реагирует изменениями своего математического ожидания или среднего зна­чения.

4. Связь случайной величины с величинами неслучайными.

Анализу последнего вида связи, который широко используют в статистических методах планирования эксперимента, посвящена данная глава. Природа связи случайной величины с величинами неслучайными может быть двоякой: а) измерения зависимой пере­менной у связаны с некоторой ошибкой измерения, а переменные x₁, х₂,…, x_k измеряются без ошибок или эти ошибки пренебрежимо малы по сравнению с ошибкой измерения зависимой переменной; б) значения переменной у зависят не только от контролируемых факторов х₁, x₂, …, x_k, но и от ряда неконтролируемых факторов, поэтому при каждом сочетании значений х₁, х₂,.... x_k зависимая переменная у подвержена колебаниям случайного характера.

Часто возникает необходимость в установлении связи между случайной величиной у и неслучайными переменными x₁, х₂,…, х_к, принимающими в каждой серии опытов определенные значения. Величина у является случайной, имеет нормальное распределение с центром распределения M[у], изменяющимся при изменении значе­ний факторов x₁, х₂, …, х_к. Случайная величина у имеет постоянную дисперсию σ², т. е. дисперсию, не зависящую от х₁,…, х₂, х_к. Мате­матическое ожидание M[y] является функцией x₁, х₂,…, х_к, т. е. на каждое изменение неслучайных величин x₁, х₂,…, х_к случайная ве­личина у реагирует изменением своего математического ожидания. Выражение М[у]=f(х₁, х₂,.... x_k) называют уравнением регрессии математического ожидания случайной величины у по неслучайным величинам x₁, х₂,…, х_к.

Тип функции М[у]=f(х₁, х₂,.... x_k) может быть линейным или криволинейным. Таким образом, в основе рег­рессионного анализа лежат следующие предположения:

1) при каждом сочетании значений x₁, х₂,…, х_к величина у име­ет нормальное распределение;

2) дисперсия σ² теоретического распределения случайной вели­чины у постоянна;

3) тип функции М[у]=f(х₁, х₂,.... x_k) известен;

4) независимые переменные x₁, х₂,…, х_к измеряются с пренебре­жимо малыми ошибками по сравнению с ошибкой в определении

5) переменные x₁, х₂,…, х_к линейно независимы.

Пусть переменная Y зависит от одной переменной x. При этом предполагается, что переменная x принимает заданные фиксированные значения, а зависимая переменна Y имеет случайный разброс из-за ошибок измерения, влияния неучтенных факторов и т.д. Каждому значению xсоответствует некоторый закон распределения вероятностей случайной величины Y. Предположим, что Y в "среднем" линейно зависит от значений переменной x. Это означает, что условное математическое ожидание случайной величины Y при заданном значении xимеет вид

.

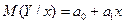Данная функция называется линейной теоретической функцией регрессии Y на x, а параметры 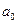и 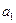– параметрами линейной регрессии (коэффициенты регрессии). На практике параметры регрессии определяются по результатам наблюдений переменных Y и x, связь между которыми можно записать

,

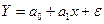где e – случайная ошибка наблюдений.