 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Носители данных
|
|
Данные — диалектическая составная часть информации. Они представляют собой зарегистрированные сигналы. При этом физический метод регистрации может быть любым: механическое перемещение физических тел, изменение их формы или параметров качества поверхности, изменение электрических, магнитных, оптических характеристик, химического состава и (или) характера химических связей, изменение состояния электронной системы и многое другое. В соответствии с методом регистрации данные могут храниться и транспортироваться на носителях различных видов.
Самым распространенным носителем данных, хотя и не самым экономичным, по-видимому, является бумага. На бумаге данные регистрируются путем изменения оптических характеристик ее поверхности. Изменение оптических свойств (изменение коэффициента отражения поверхности в определенном диапазоне длин волн) используется также в устройствах, осуществляющих запись лазерным лучом на пластмассовых носителях с отражающим покрытием (CDROM). В качестве носителей, использующих изменение магнитных свойств, можно назвать магнитные ленты и диски. Регистрация данных путем изменения химического состава поверхностных веществ носителя широко используется в фотографии. На биохимическом уровне происходит накопление и передача данных в живой природе.
Носители данных интересуют нас не сами по себе, а постольку, поскольку свойства информации весьма тесно связаны со свойствами ее носителей. Любой носитель можно характеризовать параметром разрешающей способности ( количеством данных, записанных в принятой для носителя единице измерения) и динамическим диапазоном (логарифмическим отношением интенсивности амплитуд максимального и минимального регистрируемого сигналов). От этих свойств носителя нередко зависят такие свойства информации, как полнота, доступность и достоверность. Так, например, мы можем рассчитывать на то, что в базе данных, размещаемой на компакт-диске, проще обеспечить полноту информации, чем в аналогичной по назначению базе данных, размещенной на гибком магнитном диске, поскольку в первом случае плотность записи данных на единице длины дорожки намного выше. Для обычного потребителя доступность информации в книге заметно выше, чем той же информации на компакт-диске, поскольку не все потребители обладают необходимым оборудованием. И, наконец, известно, что визуальный эффект от просмотра слайдов проекторе намного больше, чем от просмотра аналогичной иллюстрации, напечатанной на бумаге, поскольку диапазон яркостных сигналов в проходящем свете на два три порядка больше, чем в отраженном.
Задача преобразования данных с целью смены носителя относится к одной из важнейших задач информатики. В структуре стоимости вычислительных систем устройства для ввода и вывода данных, работающие с носителями информации, составляют до половины стоимости аппаратных средств.
Операции с данными
В ходе информационного процесса данные преобразуются из одного вида в другой с помощью методов. Обработка данных включает в себя множество различных операций. По мере развития научно-технического прогресса и общего усложнения связей в человеческом обществе трудозатраты на обработку данных неуклонно возрастают. Прежде всего, это связано с постоянным усложнением условий управления производством и обществом. Второй фактор, также вызывающий общее увеличение объемов обрабатываемых данных, тоже связан с научно-техническим прогрессом, а именно с быстрыми темпами появления и внедрения новых носителей данных, средств их хранения и доставки.
В структуре возможных операций с данными можно выделить следующие основные:
• сбор данных — накопление информации с целью обеспечения достаточной полноты для принятия решений;
• формализация данных — приведение данных, поступающих из разных источников, к одинаковой форме, чтобы сделать их сопоставимыми между собой, то есть повысить их уровень доступности;
• фильтрация данных — отсеивание «лишних» данных, в которых нет необходимости для принятия решений; при этом должен уменьшаться уровень «шума»,а достоверность и адекватность данных должны возрастать;
• сортировка данных — упорядочение данных по заданному признаку с целью удобства использования; повышает доступность информации;
• архивация данных — организация хранения данных в удобной и легкодоступной форме; служит для снижения экономических затрат по хранению данных и повышает общую надежность информационного процесса в целом;
• защита данных — комплекс мер, направленных на предотвращение утраты, воспроизведения и модификации данных;
• транспортировка данных — прием и передача (доставка и поставка) данных между удаленными участниками информационного процесса; при этом источник данных в информатике принято называть сервером, а потребителя — клиентом;
• преобразование данных — перевод данных из одной формы в другую или из одной структуры в другую. Преобразование данных часто связано с изменением типа носителя, например книги можно хранить в обычной бумажной форме, но можно использовать для этого и электронную форму, и микрофотопленку. Необходимость в многократном преобразовании данных возникает также при их транспортировке, особенно если она осуществляется средствами, не предназначенными для транспортировки данного вида данных. В качестве примера можно упомянуть, что для транспортировки цифровых потоков данных по каналам телефонных сетей (которые изначально были ориентированы только на передачу аналоговых сигналов в узком диапазоне частот) необходимо преобразование цифровых данных в некое подобие звуковых сигналов, чем и занимаются специальные устройства — телефонные модемы.
Приведенный здесь список типовых операций с данными далеко не полон. Миллионы людей во всем мире занимаются созданием, обработкой, преобразованием и транспортировкой данных, и на каждом рабочем месте выполняются свои специфические операции, необходимые для управления социальными, экономическими, промышленными, научными и культурными процессами. Полный список возможных операций составить невозможно, да и не нужно. Сейчас нам важен другой вывод: работа с информацией может иметь огромную трудоемкость, и ее надо автоматизировать.
Системы счисления
Система счисления (С.С.) -это способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения. В зависимости от способа изображения чисел С.С. бывают позиционные и непозиционные. В непозиционной С.С. символы, обозначающие то или иное количество, не меняют своего значения в зависимости от места в изображении количество. Примером непозиционной С.С. может служить римская, в которой для каждого числа используется специфическое сочетание символов (XIV, CXXVII и т.п.). В позиционной С.С. количественное значение каждой цифры зависит от ее места (позиции) в числе. Количество (Р) различных цифр, используемых для изображения числа в позиционной С.С., называется основанием С.С. Значения цифр лежат в пределах от 0 до Р-1. В общем случае запись любого смешанного числа в С.С. с основанием Р будет представлять собой ряд вида:
a  Р
Р  + a
+ a 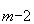 Р
Р  +...+ a
+...+ a  Р
Р  + a
+ a  Р
Р  + a
+ a 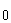 Р
Р  + a
+ a  Р
Р  + a
+ a  Р
Р  +.... + +a
+.... + +a  Р
Р  , (1)
, (1)
где нижние индексы определяют местоположение цифры в числе (разряд):
· положительные значения индексов - для целой части числа (m разрядов),
· отрицательны значения - для дробной (s разрядов).
Так, например, в общепринятой десятичной сс в последовательности цифр 777,77 одна и та же цифра 7 представляет сотни, десятки, единицы, десятые и сотые доли единицы:
777,77 = 7 * 100 + 7 * 10 + 7 *1 + 7 *  + 7 *
+ 7 * 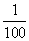 =
=
= 7 * 10  +7 *10
+7 *10  + + 7 *10
+ + 7 *10 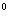 + 7 * 10
+ 7 * 10  + 7 *10
+ 7 *10  .
.
Максимальное число, которое может быть представлено в m разрядах:
N  = Р
= Р  - 1.
- 1.
Минимальное значащее число (не равное 0), которое может быть представлено в s разрядах дробной части:
N  = Р
= Р  .
.
Имея в целой части m числа, а в дробной S разрядов, можно записать всего Р  разрядных чисел.
разрядных чисел.
Двоичная С.С. имеет основание Р=2 и использует для представления информации всего две цифры: 0 и 1. Существуют правила перевода чисел из одной С.С. в другую, основанные в том числе и на соотношении (1 ). Например:
101110,101  =1*2
=1*2  +0*2
+0*2  +1*2
+1*2  +1*2
+1*2  +1*2
+1*2  +0*2
+0*2  +1*2
+1*2  +0*2
+0*2  +1*2
+1*2  = 46,625
= 46,625  .
.
Восьмеричная С.с. имеет основание Р=8 и имеет алфавит, состоящий из цифр 0...7.
257  = 2*8
= 2*8  + 2*8
+ 2*8  + 2*8
+ 2*8  = 175
= 175  .
.
В шестнадцатеричной С.с. (Р=16) используются цифры 0...9 и латинские буквы А...F (A- соответствует 10, B-11, C-12,D-13, E-14,F-15).
AF  =10*16
=10*16  + F*16
+ F*16  = 175
= 175  .
.
Вопросы перевода из одной С.С. в другую играют весьма важную роль для программистов, использующих языки программирования низкого уровня (микропрограммные, машинные, ассемблеры и др.). Рассмотрим некоторые приемы перевода чисел из одной С.С. в другую. Пусть имеются две С.С. с основаниями р и d. Любое целое число в этих С.С. можно представить соответственно в виде:
N  =
=  и N
и N  =
= 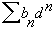 , где n = 1, 2, 3....
, где n = 1, 2, 3....
Алгоритм перевода целого числа из одной С.С. в другую состоит в следующем. На первом шаге делим в С.С. с р - основанием число N  на d - основание: N
на d - основание: N  / d = N
/ d = N 
 + a
+ a  ; на втором шаге делим число N
; на втором шаге делим число N 
 на d - основание: N
на d - основание: N 
 / d = N
/ d = N 
 + a
+ a  и т.д. Последний результат деления будет: N
и т.д. Последний результат деления будет: N 
 / d = N
/ d = N 
 + a
+ a  . Тогда нетрудно заметить, что число N
. Тогда нетрудно заметить, что число N  должно иметь вид:
должно иметь вид:
N  = N
= N  d
d  + a
+ a  d
d  +... + a
+... + a  d
d  + a
+ a  d
d  .
.
Рассмотрим теперь перевод чисел, меньших 1. В этом случае числа N  и N
и N  имеют следующий вид: N
имеют следующий вид: N  =
=  и N
и N  =
= 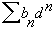 , где n = -1,-2,-3.....
, где n = -1,-2,-3.....
Алгоритм перевода дробного числа из одной С.С. в другую состоит в следующем. Hа первом шаге умножаем в С.С. с р - основанием число N  на d - основание:
на d - основание:
N  *d = b
*d = b  . N
. N 
 ; на втором шаге умножаем число N
; на втором шаге умножаем число N 
 на d - основание: N
на d - основание: N 
 *d = b
*d = b  . N
. N 
 и т.д. Следует отметить, что результатом такого умножения будет последовательность цифр b
и т.д. Следует отметить, что результатом такого умножения будет последовательность цифр b  . Тогда нетрудно заметить, что число N
. Тогда нетрудно заметить, что число N  должно иметь вид: N
должно иметь вид: N  = 0. b
= 0. b  d
d  + b
+ b  d
d  + b
+ b  d
d  +....
+....
Для перевода смешанных чисел следует отдельно переводить их целые и дробные части согласно алгоритмам. Рассмотрим пример: 10 ® 8
1942 8
16 242 8
34 240 30 8
32 2 24 3
22 6
6
| 0.55 | 0.40 | 0.20 | 0.60 | 0.80 | 0.40 |
| * 8 | * 8 | * 8 | * 8 | * 8 | * 8 |
| 4. 40 | 3. 20 | 1. 60 | 4. 80 | 6. 40 | 3. 20 |
В процессе умножения обнаружен период, равный (3146)  . Таким образом, результат перевода равен: 1942,55
. Таким образом, результат перевода равен: 1942,55  = 3626,4 (3146)
= 3626,4 (3146)  .
.
Переход от записи чисел в двоичной С.С. к восьмеричной или шестнадцатеричной и обратно осуществляется по еще более простым правилам.
Для перехода 2 ® 8 (или 16)необходимо, двигаясь справа налево, разбить двоичное число на группы по три (четыре) разряда соответственно, дополняя при необходимости левую крайнюю группу нулями. Затем каждую группу из трех (четырех) разрядов заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Для перевода восьмеричного (шестнадцатеричного) числа в двоичное достаточно заменить каждую цифру указанного числа соответствующим трехразрядным (четырехразрядным) двоичным числом. При этом ненужные слева нули отбрасываются.
В общем случае верно утверждение: если имеются две С.С. с Р  и Р
и Р  - основаниями (n = md; где m, d - целые числа), то для перевода любого числа, заданного в Р
- основаниями (n = md; где m, d - целые числа), то для перевода любого числа, заданного в Р  - С.С., в Р
- С.С., в Р  - С.С. достаточно каждую его цифру заменить Р
- С.С. достаточно каждую его цифру заменить Р  ®Р
®Р  кодом.
кодом.
В качестве примеров докажем, что 010101111  = 257
= 257  , 10101111
, 10101111  =AF
=AF  .
.
0 1 0 1 0 1 1 1 1  1 0 1 0 1 1 1 1
1 0 1 0 1 1 1 1 
2 5 7  А F
А F 
Верны и обратные переводы: 257  = 0 1 0 1 0 1 1 1 1
= 0 1 0 1 0 1 1 1 1  ,
,
AF  =1010 1111
=1010 1111  . 2 5 7
. 2 5 7
А F
Важность 8- и 16- С.С. в качестве промежуточных между двоичной и десятичной заключается в том, что каждый байт вмещает две шестнадцатеричные цифры, а ЭВМ работает с числами в двоичной С.С., кроме десятичной арифметики. Переводы же 16®2 и 2®16 можно делать посредством кодирования. Аналогично обстоит дело и с восьмеричной С.С.. Современная вычислительная техника использует, в основном, двоичную С.С. для хранения команд и информации, при выполнении арифметических и логических операций; С.С. с основаниями 8 и 16 используются для более компактной записи команд и содержимого памяти, а также при некоторых специфических форматах представления чисел.
Прямой, обратный и дополнительный коды
Специфика цифровой вычислительной техники и предъявляемые к ней требования накладывают ограничения на использование привычной нам десятичной С.С., используемой в основном для ввода/вывода информации и десятичной арифметики. Тогда как обработка информации производится, главным образом, в двоичной С.С.. Рассмотрим простейшие операции двоичной арифметики. Сложение (вычитание) двоичных чисел производится поразрядно с переносом (заниманием) единицы в старший (старшем) разряд (е):
| 1001110100111. 0110 | 11011001. 011 |
| + 10001011. 1001 | - 100110. 100 |
| 1010000110010. 1111 | 10110010. 111 |
Как и в случае десятичных чисел умножение бинарных (двоичных) чисел производится путем поразрядного умножения с последующим суммированием; положение десятичной точки определяется также аналогично. Сказанное с очевидными изменениями относится и к случаю деления бинарных (двоичных) чисел. Проиллюстрируем сказанное:
| 1011. 1 | ||
| * 101. 01 | ¾ 11001 | |
| ¾ 11001 | ||
| ¾ 11001 | ||
| 111100. 011 |
Нетрудно заметить, что операция умножения бинарных чисел сводится к операциям сдвига и сложения; деление использует последовательное вычитание. Простота правил двоичного сложения, вычитания и умножения позволяет упрощать схемы арифметических устройств ЭВМ.
С целью упрощения выполнения арифметических операций для представления числовой информации применяются специальные коды, позволяющие упрощать определение знака результата и заменять вычитание сложением.
Прямой код любого двоичного N- числа определяется следующим образом: признаком знака является наличие нуля (+) или единицы (-) в старшем разряде регистра, называемом знаковым, значащая часть числа не меняется. Например числа Х = -11011001; Y = 110111001 в прямом коде имеют вид:
Х  = 111011001 Y
= 111011001 Y  = 0110111001.
= 0110111001.
Нетрудно убедиться, что сложение в прямом коде чисел с одинаковыми знаками весьма просто - числа складываются, а содержимое знакового разряда не меняется. В случае чисел с разными знаками операция сложения в прямом коде значительно сложнее, поэтому для представления чисел со знаком используются обратный и дополнительный коды.
При использовании двух последних кодов операция сложения чисел с различными знаками сводится к операции сложения при помощи обратного и дополнительного кодов, например, числа X=1996 и Y= -54, представленные в выше изложенных кодах согласно определению принимают соответственно следующий вид:
X  =0 11111001100 =0 11111001100
| X  =0 11111001100 =0 11111001100
| X  =0 11111001100 =0 11111001100
|
Y  =1 00000110110 =1 00000110110
| Y  =1 11111001001 =1 11111001001
| Y  =1 11111001010 =1 11111001010
|
| 0 11110010110 | 0 11110010110 |
Из примера хорошо видно, что для положительного двоичного числа значения всех трех кодов совпадают; тогда как обратный код отрицательного числа получается из прямого кода путем инверсии всех его цифровых разрядов, а дополнительный - из обратного путем добавления к младшему разряду единицы. При сложении бинарных чисел, представленных в обратном (дополнительном) коде, производится сложение всех n разрядов регистра, включая знаковый; при этом в случае возникновения переноса в знаковом разряде 1 добавляется (не добавляется) к младшему разряду обратного (дополнительного) кода. Используя обратный (дополнительный) коды легко перейти от операции вычитания к сложению:
Z = X - Y = X  + (- Y)
+ (- Y)  .
.
Дата публикования: 2014-11-04; Прочитано: 1632 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
