 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Счётчики
|
|
Функциональный узел, предназначенный для подсчёта числа входных сигналов и запоминания кода этого числа соответствующими триггерами, называется счётчиком.
Дешифраторы.
Комбинационная логическая схема, преобразующая поступающий на входы код в сигнал только на одном из её выходов, называется дешифратором. Если количество двоичных разрядов дешифруемого кода обозначить через n, то число выходов дешифратора должно быть 2n.
В заключение главы рассмотрим примеры представления логических функций в базисах: 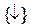 - базис Пирса (элемент Вебба);
- базис Пирса (элемент Вебба);
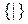 - базис Шеффера;
- базис Шеффера;
 - импликативный базис;
- импликативный базис;
{→,↛}- импликация, коимпликация;
Пример 1.
Рассмотрим представление логических функций в базисе Шеффера.
А|В = 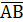 =
= 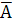 +
+ 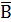
1. АВ = 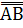 =
= 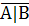 = (А|В) | (А|В)
= (А|В) | (А|В)
Проверим результат с помощью таблицы истинности:
| А | В | А|В | (А|В) | (А|В) |
2. А + В = 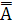 +
+ 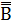 =
= 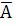 |
| 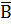 = (А|А) | (В|В)
= (А|А) | (В|В)
Результат проверить самостоятельно.
3. Логическая функция задана формулой 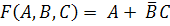 .
.
Представить заданную функцию в базисе Шеффера.
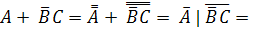 (А|А) | (
(А|А) | (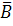 |C) = (А|А) | ((В|В)|C)
|C) = (А|А) | ((В|В)|C)
4. Логическая функция задана таблицей истинности: 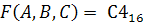 .
.
Представить заданную функцию в базисе Шеффера. Построить комбинационную схему для функции 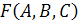 , представленной в базисе Шеффера.
, представленной в базисе Шеффера.
Решение.
1. Построим СДНФ для заданной функции:
| А | В | С | 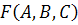
| Элементарные минтермы |
| 1* | 
| |||
| 1* | 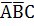
| |||
| 1* | 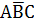
| |||
СДНФ: 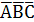 +
+ 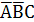 +
+ 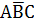 .
.
2. Упростим полученную формулу, после упрощения выполним проверку:
 +
+ 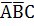 +
+ 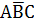 =
= 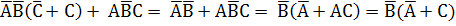
Проверка:
| А | В | С | 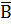
| 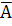
| 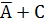
| 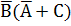
|
3. Выразим функцию 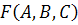 в базисе Шеффера:
в базисе Шеффера:
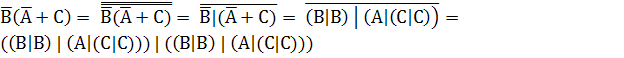 .
.
Выполним проверку:
| А | В | С | В|В | С|С | А|(С|С) | (В|В) |(А|(С|С)) | F(A,B,C) |
4. Построение комбинационной схемы.
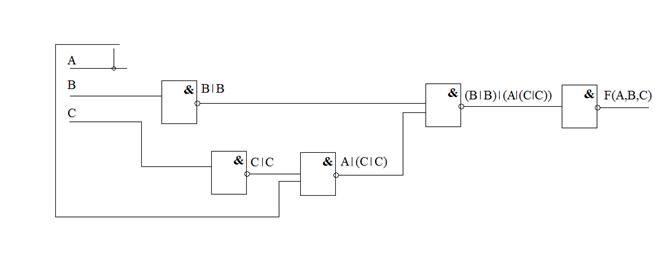
Пример 2.
Представить логическую функцию F(A,B,C) = 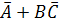 в базисе стрелка Пирса.
в базисе стрелка Пирса.
Предварительно рассмотрим, как выражаются конъюнкция и дизъюнкция через базис стрелка Пирса.
A↓B = 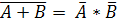
1. AB = 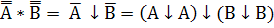
2. А+В= 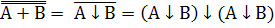
3. 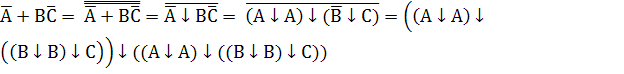
Проверку выполнить самостоятельно.
Для того чтобы выполнить проверку постройте таблицу истинности исходной функции и функции, представленной в базисе стрелка Пирса.
Пример 3.
Представить логическую функцию F(A,B,C)=А+ 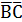 в базисе {→, 0}. Построить комбинационную схему для функции, выраженной в базисе {→, 0}.
в базисе {→, 0}. Построить комбинационную схему для функции, выраженной в базисе {→, 0}.
Рассмотрим представление отрицания, конъюнкции и дизъюнкции в базисе {→, 0}:
1. 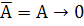
2. А*В = А* 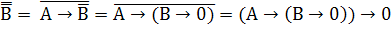
Выполним проверку:
| А | В | В 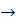 0 0
| 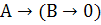
| 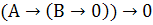
|
3. А+В = А+ 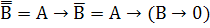
4. А+ 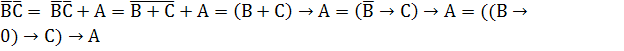
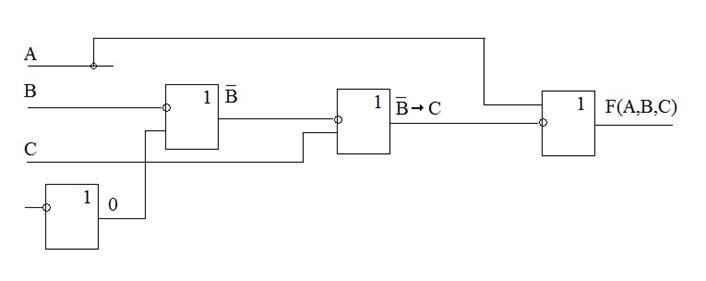
Пример 4.
Логическая функция F(A,B,C) задана таблицей истинности F(A,B,C)=В3.
Получить аналитическое представление функции в базисе {→,↛}.
Решение.
1. Получим отрицание в базисе {→,↛}. Для этого необходимо получить константу 0 или 1.
1 способ: получаем константу 0.
а) 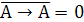
б) 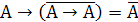
2 способ: получаем константу 1.
а) 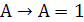
б) 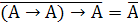
Следующие действия выполнит самостоятельно:
- получить СКНФ;
- раскрыть скобки, упростить выражение;
- записать формулу, используя операцию отрицания;
- заменить операцию отрицания, записанную в явном виде на действия, перечисленные либо в способе 1, либо в способе 2.
Дата публикования: 2014-11-04; Прочитано: 2580 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
