 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Число объектов в совокупности называется ее объемом. 224 с, 15 х 15,5 см, твердый переплет
|
|
224 с, 15 х 15,5 см, твердый переплет. Цена 135 руб.
В книге дается подробное описание следующих тренингов: «Навыки лидерства», «Этикет делового общения», «Управление конфликтом», «Развитие мотивационного потенциала сотрудников организации», «Тренинг командообразования».
Приглашаем к сотрудничеству авторов! [email protected] (812)329-08-80
Московское представительство издательства: тел. (495) 502-67-07
Издательство «Речь» (812) 323-76-70, 329-08-80 www.rech.spb.ru
Тема 1. Основные понятия математической статистики
1. Генеральная совокупность. Выборка. Выборочные значения как случайные величины.
2. Статистическое распределение выборки. Гистограмма. Эмпирическая функция распределения.
3. Числовые характеристики выборочных распределений.
1.
При исследовании реальных экономических процессов приходится обрабатывать большие объемы статистических данных по самым разнообразным показателям, которые по своей сути являются случайными величинами.
Пусть изучается совокупность однородных объектов относительно некоторого количественного признака, характеризующего эти объекты. Например, доход населения, количество покупателей в течение дня, количество качественных товаров в исследуемой партии и т.д.
Введем основные понятия, связанные с выборками.
Генеральной совокупностью называется совокупность объектов, из которых производится выборка или, другими словами, множество возможных значений случайной величины Х.
Выборочной совокупностью (или выборкой) называется совокупность случайно отобранных объектов из генеральной совокупности.
Число объектов в совокупности называется ее объемом.
Изучение всей генеральной совокупности во многих случаях либо невозможно, либо нецелесообразно в силу больших материальных затрат, уничтожения или порчи исследуемых объектов. Например, анализ среднего дохода населения какого-либо города формально предполагает наличие достоверной информации о каждом жителе города в конкретный момент времени. Получение такой информации просто невозможно. Проверка качества обуви связана с воздействием на нее различных экстремальных факторов, что приводит к потере товарного вида обуви. Поэтому на практике вся генеральная совокупность практически никогда не анализируется. Для осуществления выводов о генеральной совокупности чаще всего используется выборка ограниченного объема. В силу этого задача математической статистики состоит в исследовании свойств выборки и обобщении этих свойств на генеральную совокупность. Полученный при этом вывод называется статистическим.
Информация о генеральной совокупности, полученная на основании выборочного наблюдения, обычно обладает некоторой погрешностью, так как она основывается на изучении только части элементов выборки. Это определяет две проблемы, составляющие содержание математической теории выборки:
1) Как организовать выборочное наблюдение, чтобы полученная информация достаточно полно отражала пропорции генеральной совокупности (проблема репрезентативности выборки);
2) Как использовать результаты выборки для суждения по ним с наибольшей надежностью о свойствах и параметрах генеральной совокупности (проблема оценки).
В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если отбор будет носить случайный характер. Выборка называется репрезентативной (представительной), если по ее данным можно достаточно уверенно судить об интересующем нас признаке генеральной совокупности.
Выборку можно осуществлять двумя способами. Если после исследования объект из выборки возвращается в генеральную совокупность, то такая выборка называется повторной (возвратной ); если объект не возвращается в генеральную совокупность, то выборка называется бесповторной (безвозвратной).
2.
Установление статистических закономерностей, присущих массовым случайным явлениям, основано на изучении статистических данных – сведений о том, какие значения принял в результате наблюдений интересующий нас признак (случайная величина Х).
Различные значения признака (случайной величины Х) называются вариантами (обозначим их через х).
Рассмотрение и осмысление этих данных (особенно при большом числе наблюдений n) затруднительно, и по ним практически нельзя представить характер распределения признака (случайной величины Х).
Первый шаг к осмыслению имеющегося статистического материала – это его упорядочение. Расположение вариантов в порядке возрастания (убывания), т.е. ранжирование вариантов ряда.
Пример 1.
В таблице приведена выборка результатов измерения роста 105 студентов (юношей). Измерения проводились с точностью до 1см.
xmin=152, 155,…, 196=xmax
В таком виде изучать рост студентов тоже неудобно из-за большого числа данных. В этом случае варианты разбивают на отдельные интервалы, т.е. проводят их группировку.
Число интервалов m следует брать не очень большим, чтобы после группировки ряд не был очень громоздким, и не очень малым, чтобы не потерять особенности распределения признака. На практике обычно считают, что правильно составленный ряд распределения содержит от 6 до 15 частичных интервалов, однако фактическое число таких интервалов определяется условием задачи.
Согласно формуле Стерджеса рекомендуемое число интервалов m=1+3,322∙lg n, а величина интервала (интервальная разность, ширина интервала) 
, где хmax-xmin – разность между наибольшим и наименьшим значениями признака.
В нашем примере 
Примем k=6. За начало первого интервала рекомендуется брать величину 
или хmin.
Числа, показывающие, сколько раз встречаются варианты из данного интервала, называются частотами (обозначаются ni), а отношение их к общему числу наблюдений – частостями или относительными частотами, т.е. 
. Частоты и частости называются весами.
При изучении вариационных рядов наряду с понятием частоты, используется понятие накопленной частоты (
). Она показывает, сколько наблюдалось вариантов со значением признака, меньшим х. Отношение накопленной частоты к общему числу наблюдений назовем накопленной частостью 
. Накопленные частоты (частости) для каждого интервала находятся последовательным суммированием
Определение. Вариационным рядом называется ранжированный в порядке возрастания (или убывания) ряд вариантов с соответствующими им весами (частотами или частостями).
Пример 1. Сгруппированный ряд примера 1 представим в виде таблицы
| i | x | ni | wi | niнак | wiнак |
| 152-158 | 0,0381 | 0,0381 | |||
| 158-164 | 0,0191 | 0,0572 | |||
| 164-170 | 0,1809 | 0,2381 | |||
| 179-176 | 0,1809 | 0,4190 | |||
| 176-182 | 0,3048 | 0,7238 | |||
| 182-188 | 0,2095 | 0,9333 | |||
| 188-194 | 0,0476 | 0.9809 | |||
| 194-200 | 0,0191 | ||||
| Σ |
Для задания вариационного ряда достаточно указать варианты и соответствующие им частоты (частости) или накопленные частоты (частости).
Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и непрерывным (интервальным), если варианты могут отличаться один от другого на сколь угодно малую величину.
Ряд, представленный в примере 1 является интервальным.
Пример дискретного вариационного ряда является число покупателей в следующей задаче.
Пример 2. В супермаркете проводились наблюдения над числом Х покупателей, обратившихся в кассу за один час. Наблюдения в течение 30 часов дали следующие результаты:
70, 75,100, 120, 75, 60, 100, 120, 70, 60, 65, 100, 65, 100, 70, 75, 60, 100, 100, 120, 70, 75, 70, 120, 65, 70, 75, 70, 100, 100
Сгруппируем представленный ряд.
| № гр | ||||||
| Число покупателей | ||||||
| ni | ||||||
| wi | 3/30 | 3/30 | 7/30 | 5/30 | 8/30 | 4/30 |
| wiнак | 0,1 | 0,2 | 0,43 | 0,6 | 0,87 |
Перечень вариант и соответствующих им частот называется статистическим распределением выборки. Здесь имеется аналогия с законом распределения случайной величины: в теории вероятностей – это соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – это соответствие между наблюдаемыми вариантами и их частотами или частостями. Нетрудно видеть, что сумма относительных частот равна 1, т.е .∑ Wi=1
Весьма важным является понятие эмпирической функции распределения.
Определение. Эмпирическойфункцией распределения Fn(x) называется относительная частота (частость) того, что признак (случайная вличина X) примет значение, меньшее заданного х, т.е.
Эмпирическая функция распределения обладает теми же свойствами, что и функция распределения случайной величины в теории вероятностей:
1) Значения Fn(x) принадлежат отрезку [0; 1];
2) Fn(x) является неубывающей функцией;
3) Fn(x) =0 при x ≤ xmin, Fn(x) =1 при x ≥ xmax.
Наиболее часто вариационный ряды задаются с помощью графического изображения.
Полигон, как правило, служит для изображения дискретного вариационного ряда и представляет собой ломаную, в которой концы отрезков прямой имеют координаты (xi, ni),i=1,2,…m.
Гистограмма служит только для изображения интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака 
, i=1,2,…m, и высотами, равными частотам (частостям) ni(wi) интервалов. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон того же распределения.
Помимо полигона и гистограммы рассматривают еще один способ графического задания вариант – кумулятивная кривая – кривая накопленных частот (частостей). Для дискретного ряда кумулята представляет ломаную, соединяющую точки 
или 
. Для интервального вариационного ряда ломаная начинается с точки, абсцисса которой равна началу первого интервала, а ордината – накопленной частоте (частости), равной нулю. Другие точки этой ломаной соответствуют концам интервалов.
Пример. Построить полигон (гистограмму), кумуляту и эмпирическую функцию распределения роста студентов и числа покупателей.
Пример 1.
 |
Пример 2.
 |
Вариационный ряд содержит достаточно полную информацию об изменчивости признака. Однако обилие числовых данных, с помощью которых он задается, усложняет их использование. В то же время на практике часто оказывается достаточным знание лишь сводных характеристик вариационных рядов. Расчет статистических характеристик представляет собой второй этап обработки данных наблюдений.
3.
Одной из основных числовых характеристик ряда распределения (вариационного ряда) является средняя арифметическая.
Существует две формулы расчета средней арифметической: простая и взвешенная.
Простую среднюю арифметическую обычно используют, когда данные наблюдения не сведены в вариационный ряд либо все частоты равны единице или одинаковы 
, где xi– i- е значение признака; n – объем ряда.
Если частоты отличны друг от друга, расчет производится по формуле средней арифметической взвешенной 
, где i -е значение признака для дискретного ряда или середины интервалов интервального вариационного ряда; mi – частота i- го значения признака; k – число вариантов.
При расчете средней арифметической в качестве весов могут выступать и частости, тогда формула расчета средней арифметической взвешенной примет следующий вид: 
, где xi– i-е значение признака; k – число его значений (вариантов).
Найдем среднюю арифметическую по данным табл. примеров 1 и 2.
Решение.
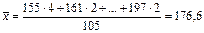, где 155, 161,…,197 – середины соответствующих интервалов.
Кроме рассмотренных средних величин, называемых аналитическими, в статистическом анализе применяются структурные, или порядковые средние. Из них наиболее широко применяются медиана и мода.
Определение. Медианой Ме вариационного ряда называется значение признака, приходящееся на середину ранжированного ряда наблюдений.
Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов – полусумме двух серединных вариантов.
Для интервального вариационного ряда находится середина ряда, а значение медианы на этом интервале находят с помощью линейного интерполирования. Отметим, что медиана может быть приближенно найдена с помощью кумуляты или графика функции распределения как значение признака, для которого = n/2 или 
=1/2.
Дата публикования: 2014-11-04; Прочитано: 475 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
